2. Модели установившихся режимов в электрических цепях и системах

В этой главе рассматриваются простые модели электрических цепей и систем, статические режимы которых рассчитываются с помощью матричных преобразований в среде MatLAB.

Приводятся вычислительные программы и решения задач, демонстрирующие эффективность использования среды в учебном процессе при проведении практикумов по различным инженерным дисциплинам.

2.1. Пример модели цепи постоянного тока

На рис 2.1 приведена разветвленная электрическая цепь.

Рис. 2.1. Разветвленная электрическая цепь постоянного тока.

Необходимо определить токи ветвей, если:

• сопротивления цепи (в омах) равны: , , , , , , ;

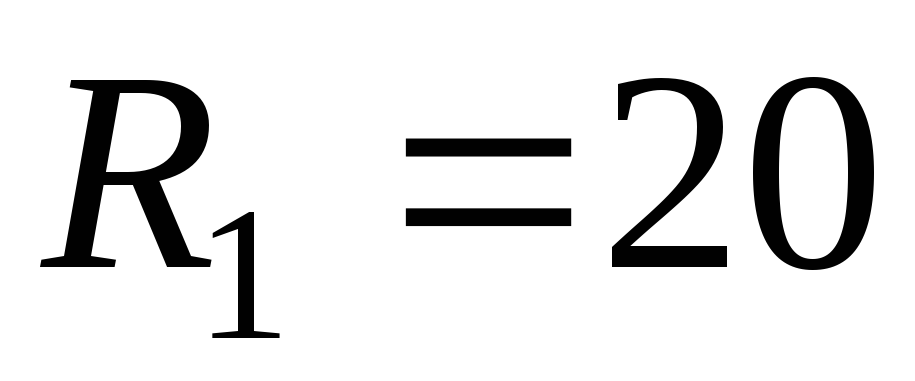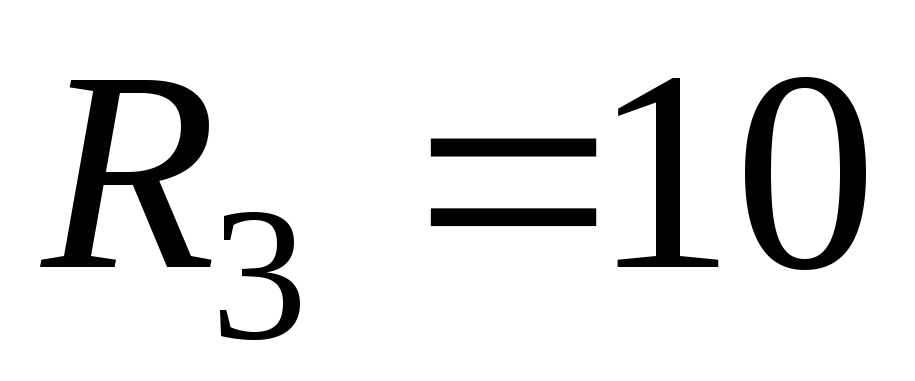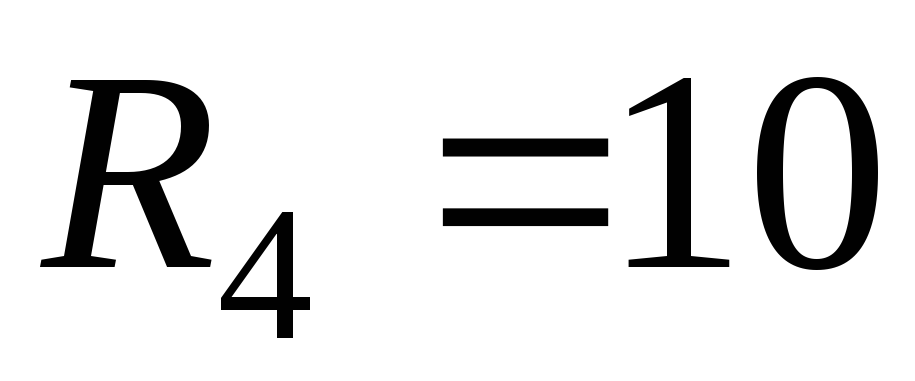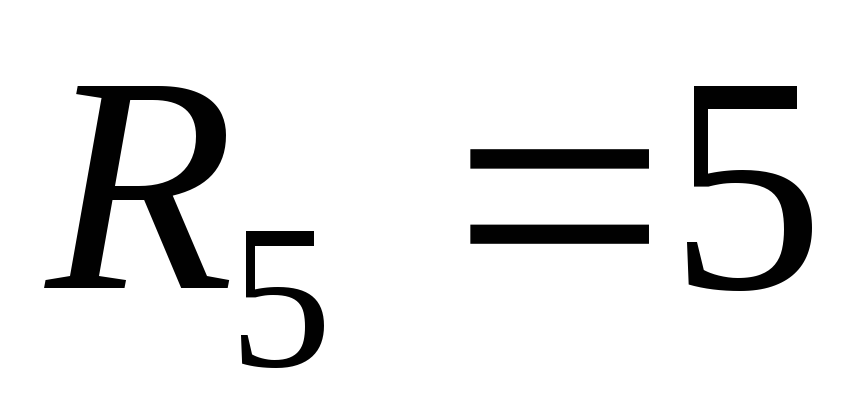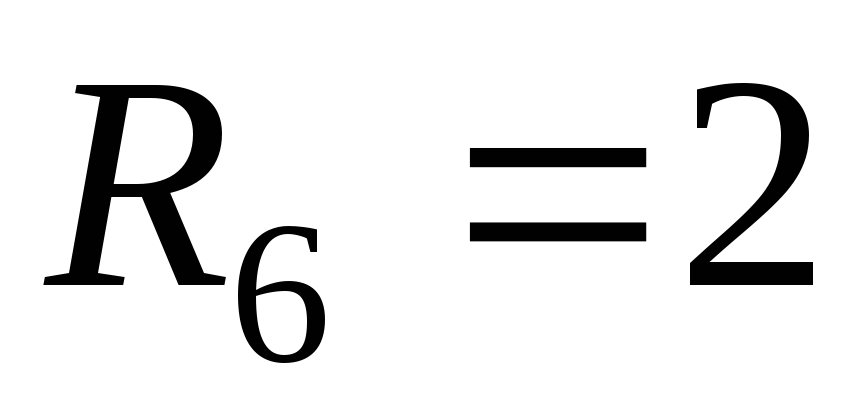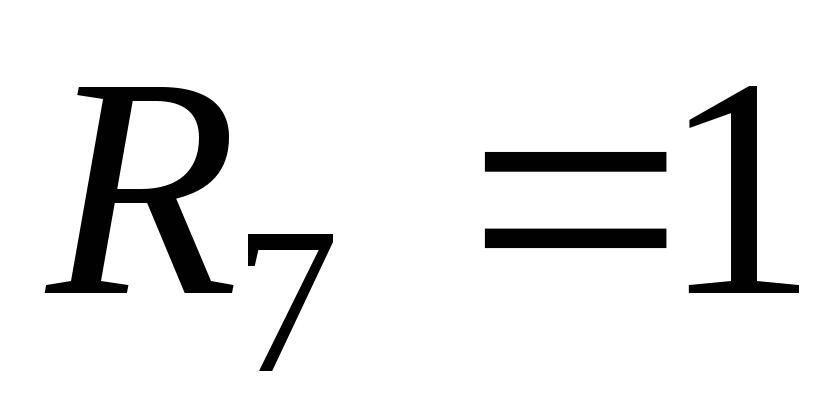• напряжения источников ЭДС (в вольтах): , , , , .

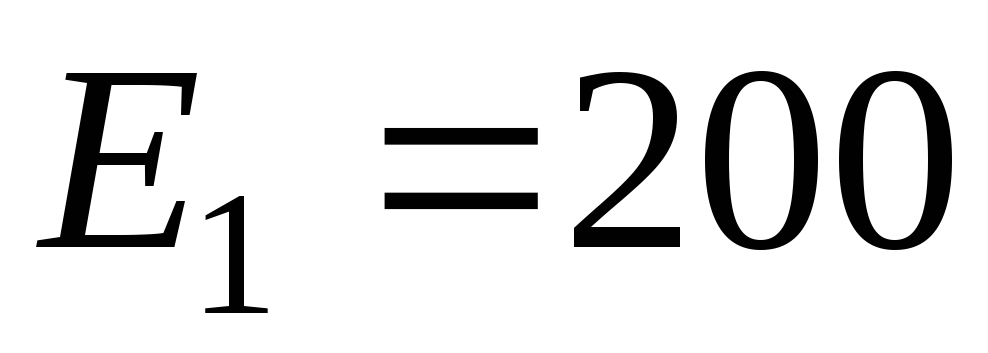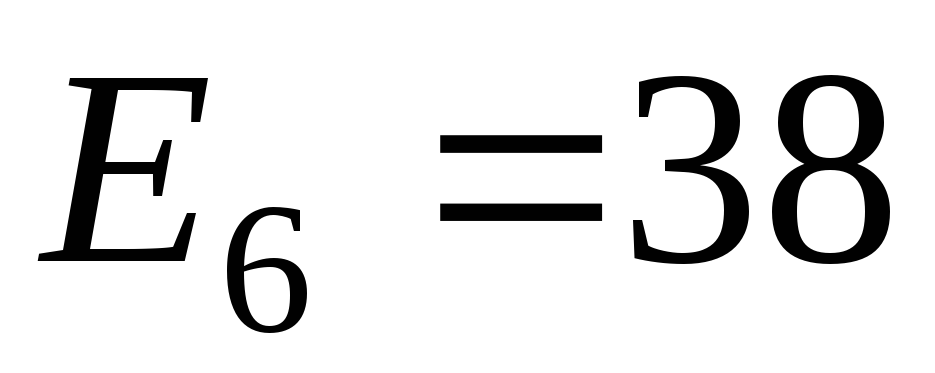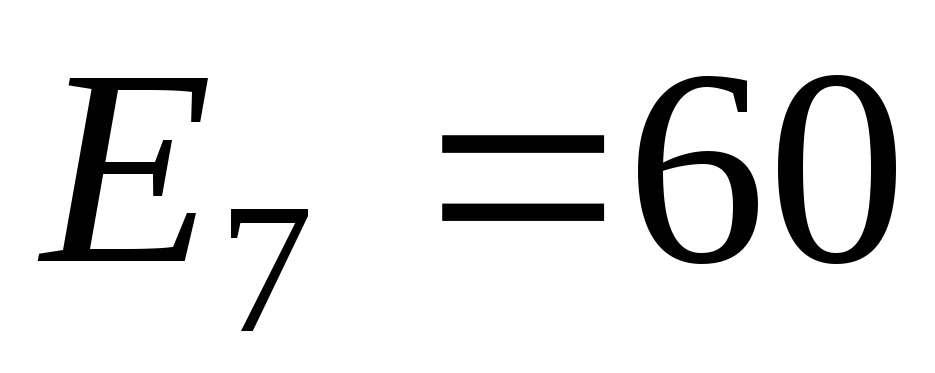К первому узлу подтекает ток , а от второго – оттекает .

Для расчета токов ветвей воспользуемся методом узловых потенциалов.

Введем вектор потенциалов узлов , приняв потенциал четвертого узла равным нулю, то есть . Зададимся токами ветвей, придав им (произвольно) направления.

Рассмотрим первый узел.

Собственная проводимость узла равна сумме проводимостей всех ветвей, подходящих к этому узлу: .

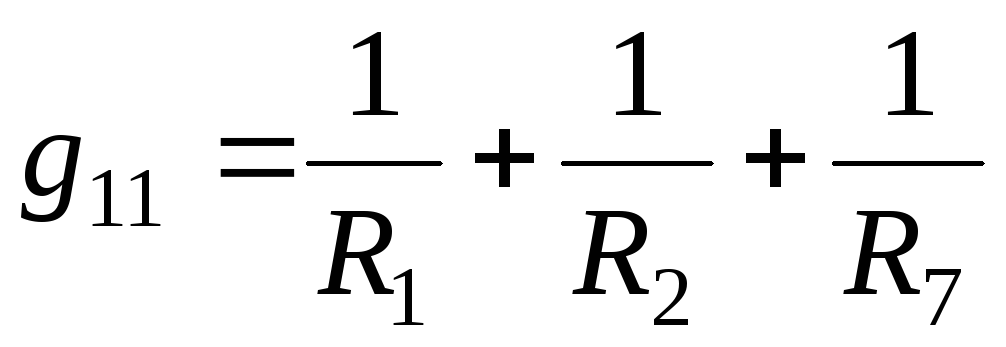Взаимные проводимости (с отрицательным знаком) равны проводимостям ветвей между узлами 1-2 и 1-3: 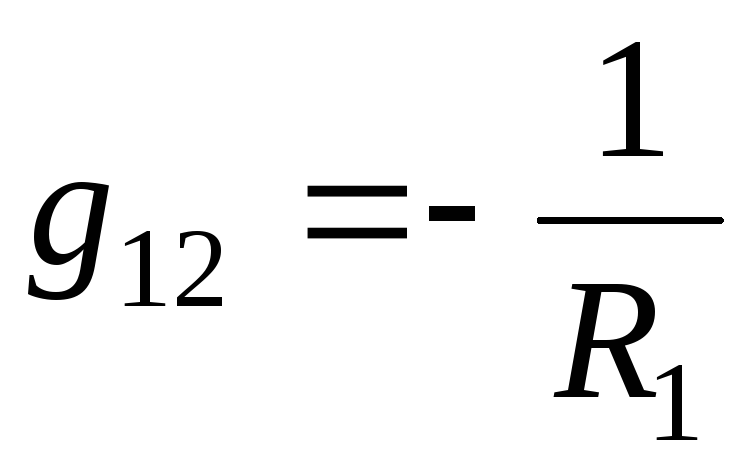и 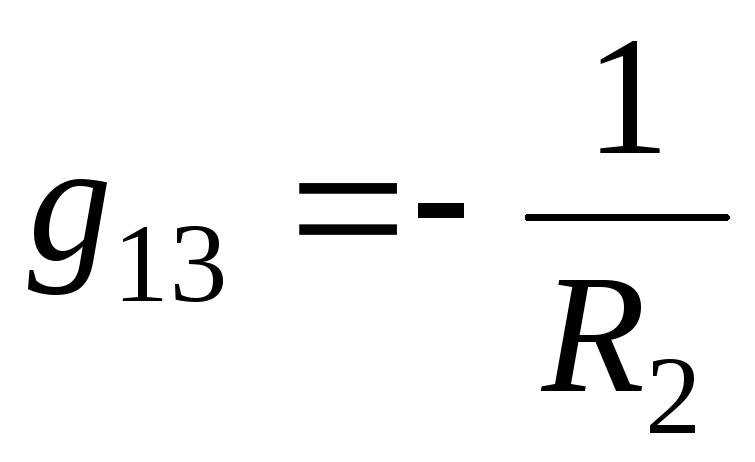. Аналогично для второго узла получим собственную проводимость . Взаимные проводимости равны: , .

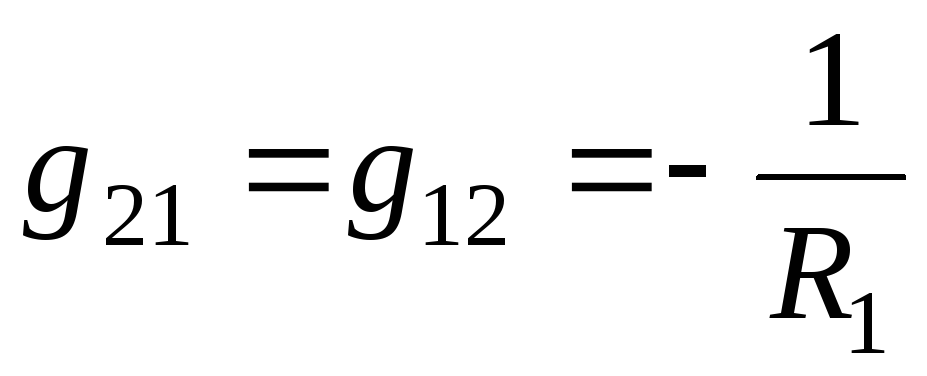Для третьего узла характерны следующие значения собственной и взаимной проводимостей: , , .

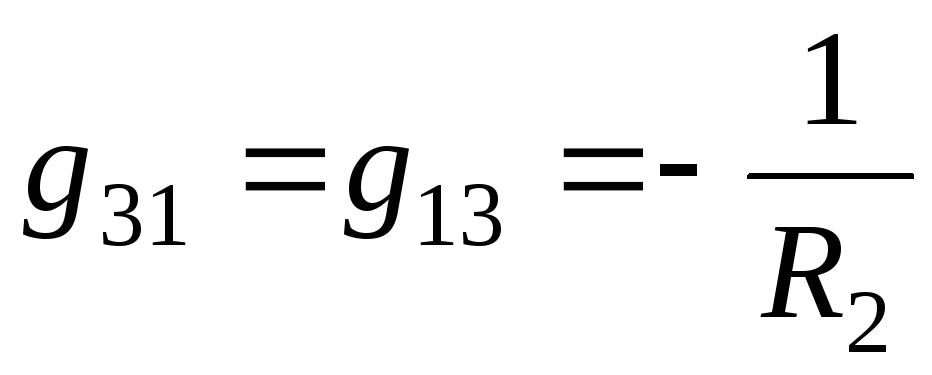Токи узлов определим по известному правилу, вытекающему из метода узловых потенциалов:

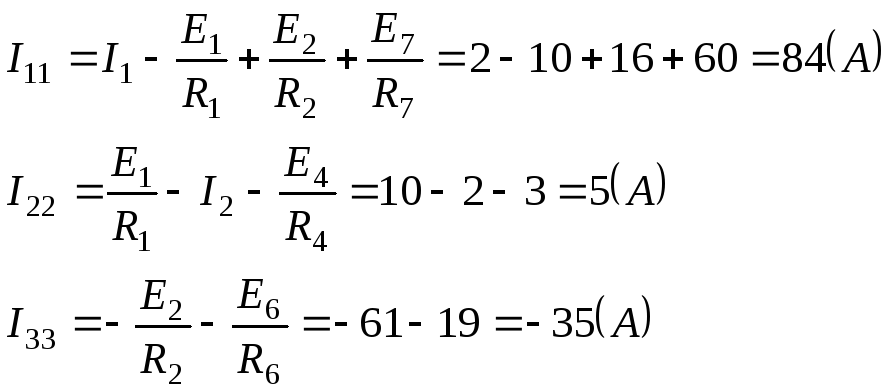
Составим уравнения в векторно-матричной форме:

, (2.0)

где матрица проводимостей равна:

, и .

Матрица является симметричной относительно главной диагонали. По этому признаку можно контролировать корректность преобразований, выполняемых в процессе расчета электрических цепей.

Получив модель цепи в виде (2.1), мы можем решить задачу непосредственно в системе MatLAB. Вектор узловых потенциалов находится путем инверсии матрицы проводимостей и умножения ее на вектор токов узлов:

(2.0)

Для определения токов в ветвях цепи воспользуемся законом Ома для обобщенной ветви. Образуем вектор:

и вектор источников ЭДС , а также диагональную матрицу проводимостей ветвей:

.

Тогда токи ветвей найдем путем решения матричного уравнения

(2.0)

Ниже приведена программа, с помощью которой определены токи ветвей. Содержание программы полностью отражает изложенную выше последовательность расчета.

Файл

%File “sah11.m”

%DC-circuit design.

%Install conditions:

r1=20; r2=5; r3=10; r4=10; r5=5; r6=2; r7=1; e1=200; e2=80; e4=30; e6=38; e7=60;

%Port potential method.

%Self and mutual conductivity

g11=1/r1+1/r2+1/r7; g12=–1/r1; g13=–1/r2;

g22=1/r1+1/r4+1/r5+1/r3; g21=g12; g23=–1/r3;

g33=1/r6+1/r3+1/r2; g31=g13; g32=g23;

%Currents of ports:

i11=2+e7/r7+e2/r2–e1/r1;

i22=–2+e1/r1–e4/r4;

i33=–e2/r2–e6/r6;

%Matrix of conductivity

G=[g11 g12 g13; g21 g22 g23; g31 g32 g33]

pause,

IVG=inv(G)

pause,

I=[i11 i22 i33]

pause,

U=IVG*I

pause

F=[U(1,1)–U(2,1), U(3,1)–U(1,1), U(2,1)–U(3,1), U(2,1), U(2,1), U(3,1),–U(1,1)];

E=[e1, e2, 0 ,e4, 0, e6, e7];

GG=[1/r1, 1/r2, 1/r3, 1/r4, 1/r5, 1/r6, 1/r7];

GD=diag(GG,0);

IV=GD*(F’+E’)

Сначала введены значения сопротивлений и величины ЭДС источников электроэнергии. Затем установлены зависимости для нахождения собственных и взаимных проводимостей; определены формулы для расчета узловых токов.

Составлена матрица , определена ее инверсия и, согласно (2.2), рассчитаны потенциалы узлов.

Шесть последних строк программы содержат операции по расчету токов с помощью уравнения (2.3).

Для проверки решения на отдельных этапах реализации программы приведем результаты вычислений:

п G =

1.2500 –0.0500 –0.2000

–0.0500 0.4500 –0.1000

–0.2000 –0.1000 0.8000

IVG =

0.8424 0.1444 0.2286

0.1444 2.3105 0.3249

0.2286 0.3249 1.3478

I =

68 5 –35

U =

50.0000

10.0000

–30.0000

IV =

12.0000

0

4.0000

4.0000

2.0000

4.0000

10.0000

п