Задание 2

Пример 4. На предприятии используется 2000 единиц оборудования определенного типа. Вероятность того, что единица оборудования откажет в течение времени Т, равна 0,002.

1. Составить ряд распределения числа единиц оборудования, отказавших в течение времени Т, указав первые четыре возможных значения.

2. Вычислить числовые характеристики распределения.

3. Вычислить вероятность того, что в течение времени Т откажет не менее трех единиц оборудования.

Решение: 1) Случайная величина Х – числа единиц оборудования, отказавших в течение времени Т, принимает значения x₀ = 0, x₁ = 1, x₂ = 2, x₃ = 3, …, x₂₀₀₀ = 2000. Первые четыре возможных значения: m = 0, 1, 2, 3. По условию задачи n = 2000, p = 0,002. Так как количество испытаний велико, а вероятность появления события А в одном испытании мала, то вероятности появления возможных значений случайной величины Х вычисляются по формуле Пуассона:

,

где = 2000∙0,002 = 4. Тогда (e^-4 ≈ 0,018 по таблице 3 приложения).

Запишем результат в таблицу:

Х	0	1	2	3	…
P(X = xi)	0,018	0,072	0,144	0,192	…

2) Вычислим числовые характеристики случайной величины Х, имеющей распределение Пуассона:

М(Х) ≈ λ = 4.

D(X) ≈ λ = 4.

σ(X) = = 2.

3) Вероятность того, что в течение времени Т откажет не менее трех единиц оборудования, вычислим, зная, что сумма всех вероятностей ряда распределения равна 1:

Р(Х 3) = Р(Х = 3) + Р(Х = 4) + … + Р(Х = 2000) =

= 1 − (Р(Х = 0) + Р(Х = 1) + Р(Х = 2)) =

= 1 − (0,018 + 0,072 + 0,144) = 1 − 0,234 = 0,766.

Ответ: 2) М(Х) = 4, D(X) = 4; σ(X) = 2. 3) Р(Х 3) = 0,766.

Пример 5. Случайная величина Х – время работы радиолампы – имеет показательное распределение.

1. Записать выражение функции распределения и плотности вероятности f(x).

2. Определить вероятность того, что время работы лампы будет не менее 600 ч, если среднее время работы радиолампы 400 ч.

Решение: 1) Воспользуемся показательным распределением, которое описывается функцией распределения следующего вида:

По условию задачи математическое ожидание случайной величины Х равно 400, следовательно, . Тогда

Плотность вероятности показательно распределенной случайной величины Х имеет следующий вид:

Таким образом, плотность вероятности запишем в виде:

2) Искомая вероятность:

Ответ:

Задание 3

Пример 6. В результате измерения диаметров 50 деталей после токарной обработки получены следующие значения (в мм):

4,20	3,80	3,99	3,82	4,23	4,03	4,06	3,94	4,24	4,16
4,10	3,84	4,18	4,03	4,17	3,91	4,15	3,98	4,12	3,85
4,28	3,93	4,01	3,93	4,15	3,96	3,70	3,89	3,91	4,11
4,01	4,11	3,98	3,79	3,78	3,99	3,93	4,02	3,92	4,09
4,08	4,29	4,01	4,03	4,05	4,03	3,98	3,95	3,95	3,90

1. Построить интервальное статистическое распределение.

2. Вычислить выборочное среднее и выборочное среднее квадратическое отклонение .

3. Построить гистограмму относительных частот.

4. С надежностью 0,95 оценить среднее значение диаметра и долю деталей, у которых диаметр не менее 4,1 мм, по всему производству.

Решение: 1) Для построения интервального ряда выполним следующие шаги:

а) определим количество интервалов где n – объем выборки

б) вычислим ширину интервала по формуле

По выборке

Следовательно, мм;

в) определим нижние – a_i и верхние – b_i границы каждого интервала. Для первого интервала: a₁ = x_min = 3,70; b₁ = a₁ + h = 3,70 + 0,1 = 3,80. Следующий интервал: [3,80; 3,90) и т.д.;

г) составим статистическое распределение, подсчитав число выборочных наблюдений по каждому интервалу. Полученные данные внесем в таблицу интервального статистического распределения.

Интервалы	[3,70-3,80)	[3,80-3,90)	[3,90-4,00)	[4,00-4,10)	[4,10-4,20)	[4,20-4,30)
Частоты	3	5	16	12	9	5

2) Выборочное среднее вычислим по формуле

,

где x_i – середина i – го интервала;

m_i – частота i – го интервала.

Интервалы	[3,70-3,80)	[3,80-3,90)	[3,90-4,00)	[4,00-4,10)	[4,10-4,20)	[4,20-4,30)
Частоты	3	5	16	12	9	5
xi	3,75	3,85	3,95	4,05	4,15	4,25

Итак,

Выборочное среднее квадратическое отклонение вычислим по формуле

3) Для построения гистограммы вычислим значения относительных частот w_i и значения плотности распределения частоты на интервале .

Интервалы	[3,70-3,80)	[3,80-3,90)	[3,90-4,00)	[4,00-4,10)	[4,10-4,20)	[4,20-4,30)
Частоты	3	5	16	12	9	5
wi	0,06	0,10	0,32	0,24	0,18	0,10
	0,6	1,00	3,20	2,40	1,80	1,00

В прямоугольной системе координат откладываем границы интервалов по оси ОХ и относительную частоту, деленную на ширину интервала по оси OY:

4) Для оценки среднего значения диаметра по всему производству воспользуемся правилом интервального оценивания генеральной средней:

,

где – предельная ошибка выборки,

По условию задачи: = 4; n = 50; σ_выб = 0,133. По таблице 2 приложения найдем – квантиль уровня функции Лапласа , т.е. . Вычислим предельную ошибку

≈ 0,37.

Следовательно, средний диаметр заключен в интервале

Для определения границ, в которых с надежностью, равной 0,95, окажется доля деталей с диаметром не менее 4,1 мм по всему производству, воспользуемся правилом интервальной оценки вероятности:

,

где – предельная ошибка выборки,

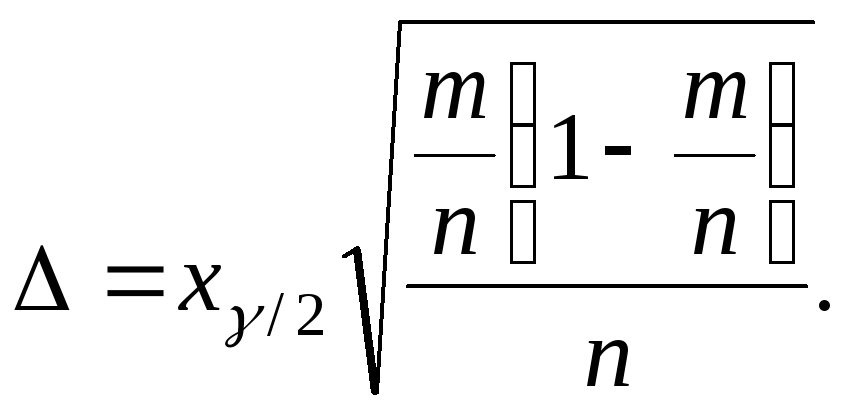
Для нашей задачи:

– доля детали с диаметром не менее 4,1 мм в выборочной совокупности;

р – доля бракованных деталей во всей партии.

Подставляем данные из условия задачи в формулу предельной ошибки выборки: m – число деталей в выборке, у которых диаметр не менее 4,1 мм, т.е. m = 14, n = 50, =1,96

≈ 0,124.

В результате получаем, что доля деталей с диаметром не менее 4,1 мм по всему производству заключена в интервале

Ответ: с надежностью 0,95 следует ожидать, что среднее значение диаметра по всему производству будет находиться в границах от 3,63 до 4,37 мм. Доля деталей с диаметром не менее 4,1 мм по всему производству будет находиться в границах от 12,6% до 40,4%.