
- •Высшая математика Кривые второго порядка Учебно-методическое пособие
- •1. Окружность. Эллипс.
- •Ключевые понятия
- •1. Окружность. Эллипс
- •(5) – Каноническое уравнение эллипса с центром в начале координат. Соответственно, уравнение
- •– Каноническое уравнение эллипса с центром в точке
- •2. Гипербола
- •Прямые называются директрисами гиперболы. –левая директриса,
- •3. Парабола
- •1. Понятие квадратичной формы и способы ее записи.
- •Ключевые понятия
- •1. Понятие квадратичной формы и способы ее записи
- •2. Знакоопределенность квадратичных форм. Критерии положительной и отрицательной определенностей
- •Критерий отрицательной определенности
- •Задачи и упражнения
- •Литература
- •Содержание
- •Минченков Юрий Владимирович высшая математика Кривые второго порядка
- •220086, Минск, ул. Славинского, 1, корп. 3.
Частный институт управления и предпринимательства
Ю. В. Минченков
Высшая математика Кривые второго порядка Учебно-методическое пособие
Минск 2006
УДК 51
ББК 22.11.я73
М 62
Рекомендовано к изданию редакционно-издательским советом
Частного института управления и предпринимательства
А в т о р
заведующий кафедрой высшей математики и статистики
Частного института управления и предпринимательства,
кандидат физико-математических наук, доцент Ю. В. Минченков
Р е ц е н з е н т
доцент кафедры высшей математики и математической физики Белорусского государственного университета,
кандидат физико-математических наук, доцент А. А. Егоров
Рассмотрено и одобрено на заседании кафедры высшей математики и статистики,
протокол № 2 от 19 сентября 2006 г.
Минченков, Ю. В.
М 62 Высшая математика. Кривые второго порядка: учеб.-метод. пособие / Ю. В. Минченков.– Минск: Частн. ин-т упр. и предпр., 2006.– 23 с.
Подготовлено в соответствии с рабочей программой ЧИУиП по дисциплине «Высшая математика». Охватывает основное содержание тем «Кривые второго порядка», «Квадратичные формы», содержит лекции, примеры, задачи для самостоятельного решения.
Предназначено для студентов Частного института управления и пред-принимательства.
УДК 51
ББК 22.11.я73

 Частный
институт управления и предпринимательства,
2006
Частный
институт управления и предпринимательства,
2006
Лекция 1. Кривые второго порядка
План
1. Окружность. Эллипс.
2. Гипербола.
3. Парабола.
Ключевые понятия
Асимптота. Гипербола. Директриса. Окружность.
Парабола. Эксцентриситет. Эллипс.
1. Окружность. Эллипс
При
рассмотрении уравнений прямой на
плоскости мы видели, что все они –
уравнения первой степени, т. е. переменные
х
и у
входят
в них
в первой степени. Рассмотрим
основные виды так называемых кривых
второго порядка, т. е. кривых, в уравнениях
которых переменная х
или переменная у,
или обе переменные х
и
у,
входят во второй степени, или же входит
произведение
х·у
(степени
складываем – получаем тоже вторую
степень).
Ранее вы уже знакомились с такими
уравнениями:
![]() –
урав-нение окружности с центром в начале
координат радиуса R;
–
урав-нение окружности с центром в начале
координат радиуса R;
![]() – уравнение
гиперболы,
– уравнение
гиперболы,
![]() – уравнение параболы. Получим такназываемые
канонические (основные) уравнения
некоторых кривых
второго порядка.
– уравнение параболы. Получим такназываемые
канонические (основные) уравнения
некоторых кривых
второго порядка.
Окружностью
называется множество точек плоскости,
равноудаленных от данной точки, называемой
ее центром. Пусть
![]() – центр
окружности.R
–
радиус окружности. Пусть
– центр
окружности.R
–
радиус окружности. Пусть
![]() – произвольная точка окружности.
Следовательно,
– произвольная точка окружности.
Следовательно,
![]() =
=
=
![]()
![]()
![]()
(1)
– уравнение окружности радиуса R
c
центром в точке с координатами
![]()
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0.
Пусть
фокусы эллипса лежат на оси Х,
причем
![]() т. е.
т. е.![]() – межфокусное расстояние эллипса.
– межфокусное расстояние эллипса.
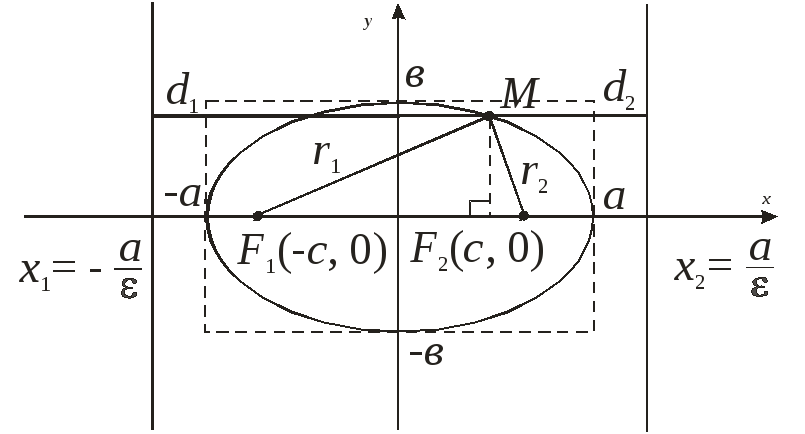
Пусть
![]() – произвольная точка эллипса. Величины
– произвольная точка эллипса. Величины![]()
![]() называютсяфокальными
радиусами
точки М
эллипса.
называютсяфокальными
радиусами
точки М
эллипса.
По определению эллипса: r1 + r2 = 2a, а > c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
 (2)
(2)
Умножим
(2) на
![]()
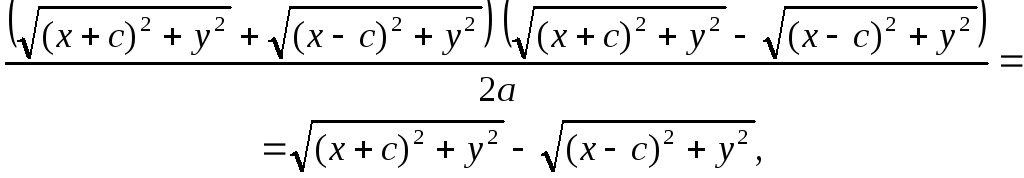
![]()
![]() (3)
(3)
Сложим уравнения (2) и (3):
![]()
![]() (4)
(4)
Возведем (4) в квадрат:
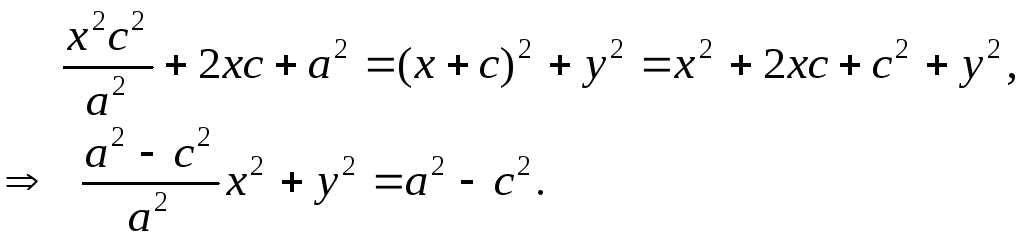
Пусть
![]()
![]()
![]() (5)
(5)
