Пример 3.1

Резиновый кубик свободно, но без зазоров вложен в стальную форму, так, что две противоположные грани свободны (рисунок 3.12). Сверху кубик подвергается давлению p. Определить напряжения и деформации кубика, а также относительное изменение объема. Модуль упругости резины - E, коэффициент Пуассона - μ. Трением между кубиком и стенками пренебречь. Стальную форму принять абсолютно жесткой (недеформируемой).

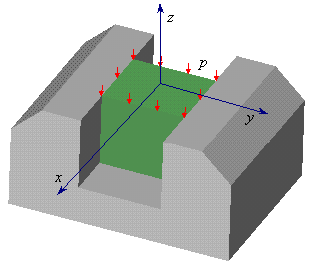
Рисунок 3.12.

Решение. По условию задачи σ_x=0, σ_z=p, ε_y=0. Используя эти условия, получим:

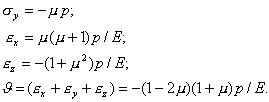
3. Растяжение-сжатие Определение внутренних усилий

Растяжением (сжатием) называется такой вид нагружения бруса, при котором из шести составляющих главного вектора и главного момента внутренних сил от нуля отличается только продольная сила.

Рассмотрим случай осевого (центрального) растяжения или сжатия, когда внешние силы действуют по оси стержня (Рисунок 4.1). Для определения внутренних усилий (продольных сил) применим метод сечений. Проведем какое-нибудь сечение, например а—а, и рассмотрим равновесие нижней отсеченной части. Воздействие верхней отброшенной части на нижнюю заменим продольной силой и предварительно направим ее от сечения, т. е. предположим, что сила является растягивающей. Составим уравнение равновесия. Проецируя все силы, действующие на нижнюю часть, на направление параллельное оси стержня, и приравнивая сумму проекций нулю, получаем

откуда

.

Знак минус показывает, что направление силы N₁ следует изменить на обратное, т. е. продольная сила будет в данном случае не растягивающей, как мы предположили, а сжимающей. Аналогично найдем продольную силу в сечении b—b: N₂=5P (растяжение). Условимся продольную силу, соответствующую растяжению считать положительной. Наглядное представление о законе изменения продольных сил по длине стержня дает график (эпюра продольных сил), ось абсцисс которого проводится параллельно оси стержня, а ось ординат ей перпендикулярна. По оси ординат в выбранном масштабе откладывают значения продольных сил (с учетом знаков) в поперечных сечениях стержня. Для рассмотренного случая эпюра N представлена на Рисунок 4.1.

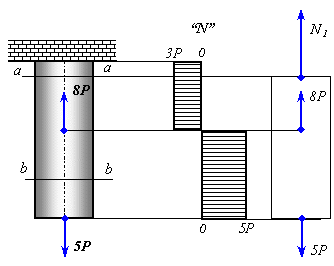
Рисунок 4.1. Эпюра продольных усилий

Определение напряжений

Если на поверхность призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стержня (рисунок 4.2, а), и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно перпендикулярными, за исключением небольшого участка стержня вблизи точки приложения силы, который из рассмотрения пока исключаем, но расстояния между ними изменятся (рисунок 4.2, б). Все горизонтальные линии, например cd, переместятся вниз, оставаясь горизонтальными и прямыми. Можно предположить также, что и внутри стержня будет такая же картина, т. е. поперечные сечения стержня, плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации. Эту важную гипотезу называют гипотезой плоских сечений или гипотезой Бернулли. Формулы, полученные на основе этой гипотезы, подтверждаются результатами опытов.

Такая картина деформаций дает основание считать, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределенные по сечению, а касательные напряжения равны нулю.

Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:

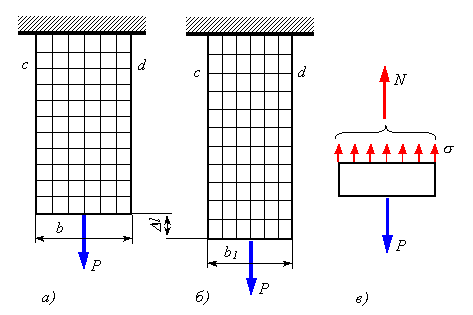
Рисунок4.2. Картина деформаций для стержня

(4.1)

Поскольку σ = const, из формулы (4.1) получим

,

(4.2)

откуда

(4.3)

В частном случае, когда на стержень действует одна внешняя сила P, из уравнения равновесия получим N=P (4.2, в). Эти формулы справедливы и для сжатия, с той только разницей, что сжимающие напряжения считаются отрицательными. Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также на устойчивость.