
- •Бийский технологический институт (филиал)
- •170104.65 – Высокоэнергетические устройства
- •160302.65 - Ракетные двигатели
- •Оглавление
- •Введение
- •Принципы сопротивления материалов Принцип Сен-Венана
- •Принцип независимости действия сил
- •Принцип начальных размеров
- •Внутренние силы. Метод сечений
- •Напряжения и деформации Напряжения
- •Связь компонентов внутренних сил с напряжениями
- •Определение напряжений на наклонных площадках
- •Определение главных напряжений и главных площадок
- •Плоское напряженное состояние
- •Графический способ определения напряжений Круги Мора
- •Графическое определение главных напряжений и положения главных площадок
- •Деформации. Деформированное состояние в точке тела
- •Обобщенный закон Гука для изотропного тела
- •Удельная потенциальная энергия деформации
- •Пример 3.1
- •Растяжение-сжатие Определение внутренних усилий
- •Определение напряжений
- •Определение деформаций и перемещений
- •Определение механических свойств материала при растяжении
- •Диаграммы условных и истинных напряжений
- •Механические характеристики материалов
- •Закон разгрузки и повторного нагружения
- •Пластичные и хрупкие материалы
- •Механические свойства при сжатии
- •Влияние температуры на механические характеристики
- •Ползучесть, последействие и релаксация
- •Длительная прочность
- •Коэффициент запаса прочности. Выбор допускаемых напряжений
- •Основные типы задач при расчете на прочность растянутых (сжатых) стержней
- •Пример 4.1
- •Пример 4.2
- •Пример 4.3
- •Анализ напряженного состояния при растяжении (сжатии)
- •Потенциальная энергия деформации при растяжении
- •Концентрация напряжений
- •Статически неопределимые задачи при растяжении и сжатии
- •Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Сдвиг (срез) Определение внутренних сил, напряжений и деформаций при сдвиге
- •Анализ напряженного состояния при сдвиге
- •Потенциальная энергия деформации при чистом сдвиге
- •Расчет на прочность при сдвиге
- •Расчет заклепочного соединения
- •Пример 5.1
- •Геометрические характеристики плоских сечений
- •Определения
- •Зависимость между моментами инерции относительно параллельных осей
- •Моменты инерции простейших фигур
- •Вычисление моментов инерции сложных фигур
- •Изменение моментов инерции при повороте осей координат
- •Главные оси и главные моменты инерции
- •Моменты сопротивления площади
- •Пример 6.1
- •Кручение Внутренние силовые факторы при кручении
- •Напряжения и деформации при кручении бруса круглого поперечного сечения
- •Напряженное состояние при кручении
- •Потенциальная энергия деформации при кручении
- •Направление вектора касательного напряжения в контурных точках сечения цилиндрического бруса
- •Кручение тонкостенного бруса замкнутого профиля
- •Кручение бруса прямоугольного сечения
- •Кручение тонкостенного бруса открытого профиля
- •Пример 7.1
- •Расчеты на прочность и жесткость при кручении
- •Пример 7.2
- •Пример 7.3
- •Пример 7.4
- •Расчет цилиндрических винтовых пружин малого шага
- •Статически неопределимые задачи при кручении
- •Плоский прямой поперечный изгиб Основные понятия и определения
- •Плоский прямой изгиб
- •Нормальные напряжения при чистом прямом изгибе
- •Касательные напряжения при плоском прямом изгибе. Формула Журавского
- •Пример 8.1
- •Пример 8.2
- •Расчеты на прочность при поперечном изгибе
- •Потенциальная энергия деформации при изгибе
- •Перемещения при изгибе Дифференциальное уравнение упругой линии балки и его интегрирование
- •Пример 8.4
- •Пример 8.5
- •Пример 8.6
- •Расчет на жесткость при изгибе
- •Определение перемещений с помощью интеграла Мора
- •Пример 8.7
- •Определение перемещений с помощью способа Верещагина
- •Пример 8.9
- •Пример 8.10
- •Определение перемещений с помощью правила «дирижера»
- •Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности
- •Гипотезы (теории) прочности
- •Критерии разрушения
- •Гипотеза наибольших нормальных напряжений (I теория прочности)
- •Гипотеза наибольших линейных деформаций (II теория прочности)
- •Критерии пластичности
- •Гипотеза наибольших касательных напряжений (III теория прочности)
- •Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности)
- •Теория прочности Мора (V теория прочности)
- •Замечания о выборе теории прочности
- •Пример 9.1
- •Пример 9.2
- •Пример 9.3
- •Пример 9.4
- •Расчет на прочность при сложном сопротивлении
- •Косой (двойной) изгиб
- •Пример 10.1
- •Внецентренное растяжение (сжатие)
- •Пример 10.2
- •Пример 10.3
- •Изгиб с кручением
- •Общий случай сложного сопротивления
- •Перемещения в пространственном брусе малой кривизны при произвольной нагрузке
- •Пример 11.1
- •Пример 11.2
- •Статически неопределимые стержневые системы Статическая неопределимость
- •Метод сил. Канонические уравнения
- •Вычисление коэффициентов канонических уравнений
- •Пример 12.1
- •Пример 12.2
- •Определение перемещений в статически неопределимых системах
- •О рациональном выборе основной системы. Использование прямой и обратной симметрии
- •Пример 12.3
- •Пример 12.4
- •Пример 12.5
- •Пример 12.6
- •Устойчивость сжатых стержней. Продольный изгиб Понятие об устойчивости первоначальной формы равновесия
- •Определение критической силы. Формула Эйлера
- •Пределы применимости формулы Эйлера
- •Устойчивость сжатых стержней за пределами упругости. Полная диаграмма критических напряжений
- •Практические способы расчета на продольный изгиб
- •Пример 13.1
- •Расчет на устойчивость с помощью коэффициента снижения основного допускаемого напряжения
- •Рациональные формы сечений сжатых стержней
- •Пример 13.2
- •Расчет элементов конструкций, движущихся с ускорением Внутренние силы, вызванные движением. Силы инерции
- •Расчет поступательно движущихся систем
- •Напряжения в тонкостенном вращающемся кольце
- •Расчет равномерно вращающегося прямого бруса
- •Вращающиеся рамы
- •Расчет на прочность при ударном действии нагрузок Удар. Основные понятия
- •Вертикальный удар
- •Пример 15.1
- •Пример 15.2
- •Пример 15.3
- •Вертикальный удар вследствие внезапной остановки движения
- •Горизонтальный удар
- •Скручивающий удар
Пример 4.4
Проверить прочность стержней и определить перемещение узла A под действием груза P=3·104 Н. Дано: α=30°, l2=1 м, [σ]=160 МПа, E=2·105 МПа, F=1 см2. Материал и сечения стержней одинаковы (Рисунок4.23).

Рисунок 4.23
Система один раз статически неопределима, так как для вычисления усилий в трех ее стержнях можно составить лишь два независимых уравнения равновесия узла A.
Статическая сторона задачи.
![]()
![]()
Геометрическая сторона задачи (условия совместности деформаций).
Система после деформации показана на Рисунок 4.23. Удлинение крайнего стержня можно найти графически, проведя дугу радиуса AB с центром в точке B. Вследствие малости деформаций дугу этой окружности можно заменить перпендикуляром, опущенным из точки A на новое положение стержня. Изменениями угла α пренебрегаем, так как оно незначительно. Рассматривая заштрихованный прямоугольный треугольник, найдем связь между удлинениями первого и второго стержня:
![]() .
.
Физическая сторона задачи.
Согласно закону Гука:
![]() ,
,
с учетом уравнения совместности деформаций, имеем:
![]() или
или
![]() .
.
Решая совместно уравнения равновесия и уравнение совместности деформаций, находим усилия в стержнях:
![]() ;
;
![]() .
.
Наибольшее напряжение действует во втором стержне:
![]() ,
,
что меньше заданного допускаемого напряжения [σ]=160 МПа. Перемещение узла A равно удлинению второго стержня:
![]() .
.
Пример 4.5
Определить напряжения в стержнях, возникающие в результате повышения температуры всех стержней на Δt=100оС (Рисунок 4.24).Балка считается абсолютно жесткой. Дано:
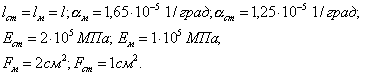
Статическая сторона задачи.
![]() .
.
Геометрическая сторона задачи (условия совместности деформаций).
В результате термического расширения стержней балка займет положение, показанное на рисунок 4.24. Исходя из этого построения, легко составить условие совместности деформаций:
![]() .
.
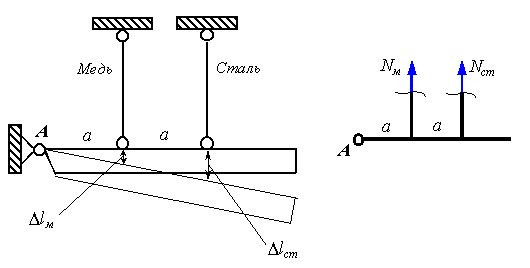
Рисунок 4.24
Физическая сторона задачи.
У медного стержня коэффициент температурного расширения больше, чем у стального. По этой причине медный стержень удлинился бы больше, чем стальной, если бы они деформировались отдельно. Но так как они связаны абсолютно жесткой балкой, то медный стержень, удлиняясь за счет термического воздействия, будет одновременно сокращаться за счет механического воздействия со стороны балки. Стальной стержень будет удлиняться как за счет термического расширения, так и за счет механического действия крайних стержней. Таким образом, абсолютная деформация стержней может быть представлена как сумма силовой и температурной деформаций:
![]() ,
,
![]() .
.
Решая данные уравнения совместно с уравнениями равновесия и геометрическими соотношениями, получим:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пример 4.6
Определить напряжения в стержнях, возникающие при сборке узла A из-за неточности изготовления стержней (Рисунок 4.25). Дано: F1=F2=F, E1=E2=E=2·105 МПа; l1=l2=l=1 м; α=30°, δ=1 мм.
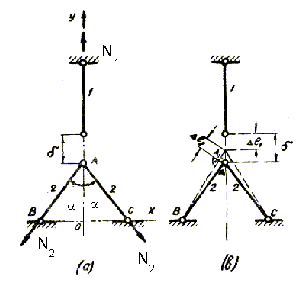
Рисунок 4.25
Статическая сторона задачи.
![]() .
.
Геометрическая сторона задачи (условия совместности деформаций).
Предположим, что после соединения, шарнир A займет положение A1 (Рисунок 4.25). Исходя из этого построения, можно составить условие совместности деформаций:
![]() .
.
Строго говоря, удлинение Δl2 получается, если из точки B описать дугу радиуса l2, однако в силу малости деформаций, Δl2 можно получить, опуская перпендикуляр из точки A на новое направление стержня l2. В собранном состоянии угол между стержнями будет меньше, чем 2α. Однако, в силу малости деформаций, изменение угла отразится на пятом или шестом знаке косинуса, что не существенно.
Физическая сторона задачи.
Согласно закона Гука:
![]() .
.
Решая совместно систему уравнений, получим:
![]()
![]()
![]()
![]()
