Пример 8.4

Для консольной балки с сосредоточенной парой M_o на свободном конце найти аналитические выражения для прогибов и углов поворота (рисунок8.24).

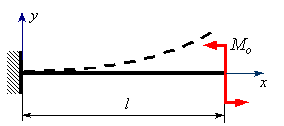
Рисунок 8.24.

По уравнениям (8.29) - (8.31) имеем

.

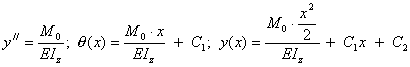В заделке прогиб y(0) и угол поворота сечения θ(0) равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Следовательно, балка изогнется по дуге параболы:

.

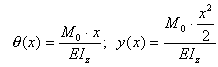На этом примере наглядно проявляется приближенный характер уравнения (8.29), так как при постоянном изгибающем моменте согласно равенству

балка должна изгибаться по дуге окружности радиуса ρ. Однако в пределах длины балки указанные дуги окружности и параболы практически совпадают.

Пример 8.5

Для консольной балки с сосредоточенной силой P на свободном конце найти аналитические выражения для прогибов и углов поворота (рисунок8.25).

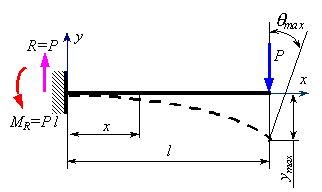
Рисунок 8.25.

Реактивная сила и момент в заделке равны R=P, M_R=Pl. В произвольном сечении на расстоянии x от заделки имеем

.

В заделке прогиб y(0) и угол поворота сечения θ(0) равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Окончательно, имеем

.

Максимальные прогиб и угол поворота будут на правом свободном конце балки:

.

(8.32).

Знак минус в формулах для прогиба и угла поворота означает, что прогиб конца консольной балки направлен вниз, а поворот концевого сечения – по часовой стрелке.

Пример 8.6

Для балки нагруженной распределенной нагрузкой найти аналитические выражения для прогибов и углов поворота (рисунок 8.26).

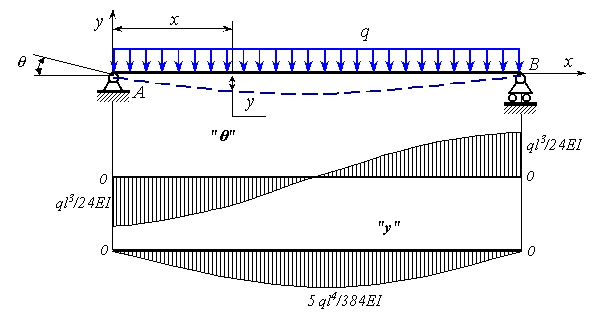
Рисунок 8.26.

Изгибающий момент в произвольном поперечном сечении

.

В произвольном сечении на расстоянии x от опоры A имеем

.

(8.33)

Из условия для прогиба на левой опоре

.

Из условия для прогиба на правой опоре

.

Подставив значения C₁ и C₂ в уравнение (8.33), получим

.

(8.34)

На рисунок 8.26 построены эпюры прогибов и углов поворота, из которых видно, что максимальный прогиб будет в середине балки

.

Максимальные углы поворота будут в опорных сечениях:

.

Расчет на жесткость при изгибе

В практических расчетах нередки случаи, когда в балке, сечение которой выбрано из условия прочности, перемещения оказываются большими – превышающими установленные для них нормы. Поэтому, кроме расчета на прочность, балки должны проверяться также и на жесткость. Обозначив допускаемую стрелу прогиба через [f], получим условие жесткости балки

.

(8.35)

Допускаемые значения стрелы прогиба зависят от назначения конструкции и колеблются в достаточно широких пределах. Так, например, в строительных конструкциях допускаемые значения относительных прогибов [f / l] колеблются от 1/150 до 1/400. При расчете валов допускаемый относительный прогиб обычно ограничивается 1/1000.

Определение перемещений с помощью интеграла Мора

Кроме способов определения перемещений сечений балок, основанных на интегрировании дифференциального уравнения упругой линии, существуют более удобные для практических целей энергетические методы. Одним из них является способ определения прогибов и углов поворотов сечений при упругих деформациях балок с помощью интеграла Мора. Этот интеграл может быть получен различными путями, и, в частности, исходя из условия равенства работы внешних сил А и потенциальной энергии U, накопленной в деформированной балке.

Определим, например, прогиб в точке С оси балки, нагруженной некоторой системой внешних поперечных сил и пар. Для упрощения промежуточных выкладок представим всю эту нагрузку одной сосредоточенной силой Р (рисунок 8.27). Обозначим через δ_PP прогиб балки в точке приложения силы Р, а через δ_CP - искомый прогиб от этой силы в точке С.

При статическом приложении к балке сила Р произведет работу

.

Потенциальная энергия деформации для первого состояния балки, если пренебречь влиянием перерезывающих сил Q на прогибы, может быть подсчитана по формуле (8.22), т. е.

.

(8.36)

Составляя баланс энергий A=U, получаем

.

(8.37)

Поступим далее следующим образом. Снимем с балки всю заданную нагрузку и приложим статически в сечении С в направлении искомого прогиба вспомогательную силу, равную по величине единице измерения силы, например, 1Н. От этой единичной нагрузки в сечениях балки возникнут изгибающие моменты M_z¹, а точка C в процессе деформации балки пройдет путь δ_C1 (см. рисунок 8.27). Баланс энергий во втором состоянии балки запишется так

.

(8.38)

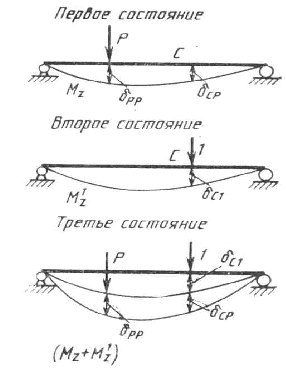
Рисунок 8.27

Рассмотрим третье состояние, когда к балке, уже нагруженной вспомогательной единичной силой, прикладывается еще и заданная нагрузка Р (см. рисунок 8.27). Эта нагрузка вызовет дополнительные деформации балки, причем согласно принципу независимости действия сил дополнительные прогибы будут такими же, как и в первом из рассмотренных состояний балки, когда она нагружена только силой Р. Поэтому работа внешних сил, если подсчитывать ее в последовательности их приложения,

.

(8.39)

У последнего слагаемого множитель 1/2 отсутствует потому, что к моменту приложения заданной нагрузки единичная сила достигла уже своего конечного значения и в процессе перемещения δ_CP величины своей не изменяет (рисунок 8.28).

Изгибающие моменты в сечениях балки в ее третьем состоянии равны суммам изгибающих моментов M_z от заданных нагрузок и M_z¹ от единичной силы, а потенциальная энергия деформации

.

(8.40)

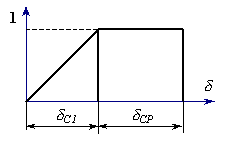
Рисунок 8.28.

Баланс энергий в третьем состоянии

(8.41)

Учитывая выражения для балансов энергий в первом и втором состояниях, получаем

.

(8.42)

Чтобы левая часть равенства представляла собой непосредственно искомый прогиб балки, нужно разделить обе части этого равенства на вспомогательную единичную силу или считать ее безразмерной. В обоих случаях получаем для определения прогибов балки выражение

,

(8.43)

где M_z¹ имеет размерность длины.

Задача определения угла поворота сечения С приводит к тому же выражению (8.43). Отличие заключается в том, что в этом случае в сечении С надо прикладывать в направлении искомого углового перемещения единичный момент, а под δ_CP понимать угол поворота сечения в радианах.

В выражении (8.43) интеграл должен быть распространен на всю длину балки. Если балка имеет п участков с различными аналитическими выражениями для изгибающих моментов M_z(x) и M_z¹(x), то в правой части будет стоять сумма интегралов по всем п участкам.

Итак, прогибы и углы поворотов сечений балок могут быть найдены из равенства, называемого интегралом Мора:

,

(8.44)

где M_z(x) - изгибающий момент в текущем сечении балки от заданной нагрузки; M_z¹(x) - изгибающий момент в том же сечении от единичной силы, если ищется прогиб, и единичного момента, если ищется угол поворота сечения.

Для определения M_z¹(x) надо снять с балки заданную нагрузку (но не удалять опоры) и приложить в том сечении, перемещение которого ищется, в направлении этого перемещения единичную силу или пару. Моменты M_z(x) и M_z¹(x) надо подставлять в интеграл Мора с их знаками. Положительный знак в окончательном выражении означает, что сечение перемещается по направлению приложенной единичной нагрузки, а отрицательный знак показывает, что перемещение происходит в противоположном направлении.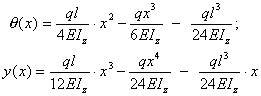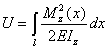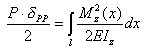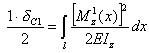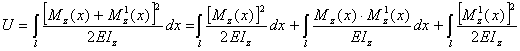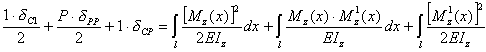
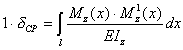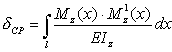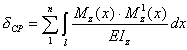