
- •Бийский технологический институт (филиал)
- •170104.65 – Высокоэнергетические устройства
- •160302.65 - Ракетные двигатели
- •Оглавление
- •Введение
- •Принципы сопротивления материалов Принцип Сен-Венана
- •Принцип независимости действия сил
- •Принцип начальных размеров
- •Внутренние силы. Метод сечений
- •Напряжения и деформации Напряжения
- •Связь компонентов внутренних сил с напряжениями
- •Определение напряжений на наклонных площадках
- •Определение главных напряжений и главных площадок
- •Плоское напряженное состояние
- •Графический способ определения напряжений Круги Мора
- •Графическое определение главных напряжений и положения главных площадок
- •Деформации. Деформированное состояние в точке тела
- •Обобщенный закон Гука для изотропного тела
- •Удельная потенциальная энергия деформации
- •Пример 3.1
- •Растяжение-сжатие Определение внутренних усилий
- •Определение напряжений
- •Определение деформаций и перемещений
- •Определение механических свойств материала при растяжении
- •Диаграммы условных и истинных напряжений
- •Механические характеристики материалов
- •Закон разгрузки и повторного нагружения
- •Пластичные и хрупкие материалы
- •Механические свойства при сжатии
- •Влияние температуры на механические характеристики
- •Ползучесть, последействие и релаксация
- •Длительная прочность
- •Коэффициент запаса прочности. Выбор допускаемых напряжений
- •Основные типы задач при расчете на прочность растянутых (сжатых) стержней
- •Пример 4.1
- •Пример 4.2
- •Пример 4.3
- •Анализ напряженного состояния при растяжении (сжатии)
- •Потенциальная энергия деформации при растяжении
- •Концентрация напряжений
- •Статически неопределимые задачи при растяжении и сжатии
- •Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Сдвиг (срез) Определение внутренних сил, напряжений и деформаций при сдвиге
- •Анализ напряженного состояния при сдвиге
- •Потенциальная энергия деформации при чистом сдвиге
- •Расчет на прочность при сдвиге
- •Расчет заклепочного соединения
- •Пример 5.1
- •Геометрические характеристики плоских сечений
- •Определения
- •Зависимость между моментами инерции относительно параллельных осей
- •Моменты инерции простейших фигур
- •Вычисление моментов инерции сложных фигур
- •Изменение моментов инерции при повороте осей координат
- •Главные оси и главные моменты инерции
- •Моменты сопротивления площади
- •Пример 6.1
- •Кручение Внутренние силовые факторы при кручении
- •Напряжения и деформации при кручении бруса круглого поперечного сечения
- •Напряженное состояние при кручении
- •Потенциальная энергия деформации при кручении
- •Направление вектора касательного напряжения в контурных точках сечения цилиндрического бруса
- •Кручение тонкостенного бруса замкнутого профиля
- •Кручение бруса прямоугольного сечения
- •Кручение тонкостенного бруса открытого профиля
- •Пример 7.1
- •Расчеты на прочность и жесткость при кручении
- •Пример 7.2
- •Пример 7.3
- •Пример 7.4
- •Расчет цилиндрических винтовых пружин малого шага
- •Статически неопределимые задачи при кручении
- •Плоский прямой поперечный изгиб Основные понятия и определения
- •Плоский прямой изгиб
- •Нормальные напряжения при чистом прямом изгибе
- •Касательные напряжения при плоском прямом изгибе. Формула Журавского
- •Пример 8.1
- •Пример 8.2
- •Расчеты на прочность при поперечном изгибе
- •Потенциальная энергия деформации при изгибе
- •Перемещения при изгибе Дифференциальное уравнение упругой линии балки и его интегрирование
- •Пример 8.4
- •Пример 8.5
- •Пример 8.6
- •Расчет на жесткость при изгибе
- •Определение перемещений с помощью интеграла Мора
- •Пример 8.7
- •Определение перемещений с помощью способа Верещагина
- •Пример 8.9
- •Пример 8.10
- •Определение перемещений с помощью правила «дирижера»
- •Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности
- •Гипотезы (теории) прочности
- •Критерии разрушения
- •Гипотеза наибольших нормальных напряжений (I теория прочности)
- •Гипотеза наибольших линейных деформаций (II теория прочности)
- •Критерии пластичности
- •Гипотеза наибольших касательных напряжений (III теория прочности)
- •Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности)
- •Теория прочности Мора (V теория прочности)
- •Замечания о выборе теории прочности
- •Пример 9.1
- •Пример 9.2
- •Пример 9.3
- •Пример 9.4
- •Расчет на прочность при сложном сопротивлении
- •Косой (двойной) изгиб
- •Пример 10.1
- •Внецентренное растяжение (сжатие)
- •Пример 10.2
- •Пример 10.3
- •Изгиб с кручением
- •Общий случай сложного сопротивления
- •Перемещения в пространственном брусе малой кривизны при произвольной нагрузке
- •Пример 11.1
- •Пример 11.2
- •Статически неопределимые стержневые системы Статическая неопределимость
- •Метод сил. Канонические уравнения
- •Вычисление коэффициентов канонических уравнений
- •Пример 12.1
- •Пример 12.2
- •Определение перемещений в статически неопределимых системах
- •О рациональном выборе основной системы. Использование прямой и обратной симметрии
- •Пример 12.3
- •Пример 12.4
- •Пример 12.5
- •Пример 12.6
- •Устойчивость сжатых стержней. Продольный изгиб Понятие об устойчивости первоначальной формы равновесия
- •Определение критической силы. Формула Эйлера
- •Пределы применимости формулы Эйлера
- •Устойчивость сжатых стержней за пределами упругости. Полная диаграмма критических напряжений
- •Практические способы расчета на продольный изгиб
- •Пример 13.1
- •Расчет на устойчивость с помощью коэффициента снижения основного допускаемого напряжения
- •Рациональные формы сечений сжатых стержней
- •Пример 13.2
- •Расчет элементов конструкций, движущихся с ускорением Внутренние силы, вызванные движением. Силы инерции
- •Расчет поступательно движущихся систем
- •Напряжения в тонкостенном вращающемся кольце
- •Расчет равномерно вращающегося прямого бруса
- •Вращающиеся рамы
- •Расчет на прочность при ударном действии нагрузок Удар. Основные понятия
- •Вертикальный удар
- •Пример 15.1
- •Пример 15.2
- •Пример 15.3
- •Вертикальный удар вследствие внезапной остановки движения
- •Горизонтальный удар
- •Скручивающий удар
Моменты сопротивления площади
Осевым моментом сопротивления площади сечения F относительно главной центральной оси называется отношение момента инерции площади относительно этой же оси к расстоянию до наиболее удаленной точки от этой оси
|
(6.34) |
Размерность момента сопротивления – [м3]. Отношение полярного момента инерции площади сечения к наибольшему радиусу – вектору этой площади, называется полярным моментом сопротивления
|
(6.35) |
Для площади прямоугольника
![]() .
.
Для площади круга
![]() .
.
Отсюда
![]() .
.
Пример 6.1
Определить положение центра тяжести полукруга (рисунок 6.2).
Решение. Направим ось y по оси симметрии полукруга, а ось z совместим с его основанием. В этом случае zc=0, надо определить только координату yc. Подсчитаем Sz непосредственным интегрированием по площади полукруга:
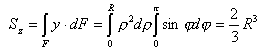 .
.
Далее по формуле (6.4) находим расстояние центра тяжести от основания полукруга:
![]() .
.
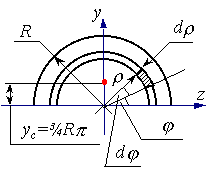
Рисунок 6.2.
Кручение Внутренние силовые факторы при кручении
Кручением называется такой вид нагружения бруса, при котором из шести составляющих главного вектора и главного момента внутренних сил от нуля отличается только крутящий момент.
При кручении бруса его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса. Вызывается кручение парами сосредоточенных и распределенных вдоль оси бруса сил, действующих в плоскостях, перпендикулярных этой оси. Брус, работающий на кручение, называется валом. Моменты, вызывающие деформацию кручения, называются крутящими моментами. Величина крутящего момента, действующего в каком-либо сечении вала, определяется методом сечений (см. рисунок 7.1). Величина крутящего момента может быть задана мощностью, передаваемой на вал, например через шкив:
|
(7.1) |
где N - мощность, передаваемая на вал [Ватт]; ω [1/сек] – круговая частота вращения вала; n - число оборотов вала [об/мин]. Если мощность задан в лошадиных силах, для перевода в систему Си следует помнить, что 1 л.с. = 736 Ватт.
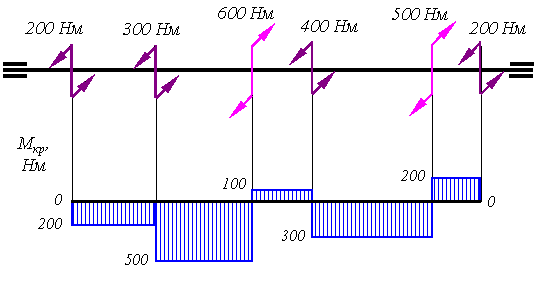
Рисунок 7.1.
Напряжения и деформации при кручении бруса круглого поперечного сечения
Под действием внешнего скручивающего момента, приложенного на правом конце вала (рисунок 7.2), левый конец которого жестко закреплен, стержень будет закручиваться. При этом любое сечение стержня, оставаясь плоским, будет поворачиваться на некоторый угол φк, называемый углом закручивания. Этот угол изменяется по длине вала от нуля в заделке до максимального на правом конце вала. При этом образующая внешней цилиндрической поверхности вала повернется на угол γ, называемый углом сдвига. Этот угол изменяется вдоль радиуса сечения от нуля на оси вала до - γmax на внешней поверхности. Опыт показывает, что после закручивания бруса круглого сечения поперечные линии, нанесенные на его поверхности, остаются плоскими, а диаметры сечений и расстояния между ними не изменяются. При этом прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений – и в продольных его сечениях, то есть напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. На основании опыта вводятся следующие гипотезы:
Нормальные напряжения в поперечных сечениях отсутствуют (иначе изменялись бы расстояния между сечениями).
Поперечные сечения при кручении остаются плоскими.
Радиусы в поперечных сечениях остаются прямолинейными (не искривляются).
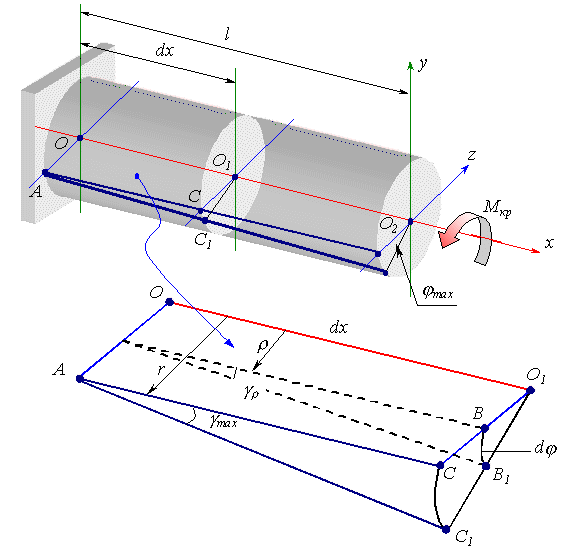
Рисунок 7.2.
С учетом указанных гипотез геометрическая картина деформаций вала представлена на рисунок 7.2. Рассмотрим, вырезанный из вала клиновидный элемент (см. рисунок 7.2) длиной dx. Из рисунка видно, что
![]()
|
(7.2) |
откуда следует, что угол сдвига изменяется по радиусу вала по линейному закону.
Согласно закону Гука при сдвиге (3.34), имеем:
откуда получаем:
|
(7.3) |
что касательные напряжения в сечении вала изменяются по радиусу по линейному закону.
При чистом кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – крутящему моменту относительно нормальной к сечению оси. Касательные напряжения перпендикулярны радиусам, проведенным через точки их действия (рисунок 7.3).
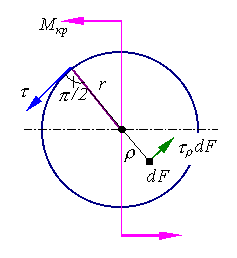
Рисунок 7.3.
Для доказательства этого будем исходить от противного, то есть, предположим, что касательное напряжение не перпендикулярно радиусу. Это означает, что в каждой точке сечения, кроме касательных напряжений, перпендикулярных радиусам, действуют радиально направленные касательные напряжения. Но если это так, то по закону парности и на цилиндрической поверхности радиуса ρ или r будет действовать касательное напряжение, что неверно, так как на боковой поверхности нет напряжений.
Крутящий момент в сечении бруса определяется из уравнения (3.5):
![]()
или в более краткой записи
|
(7.4) |
где ρ - плечо элементарной касательной силы τ
|
(7.5) |
где
![]() -
есть полярный момент инерции сечения.
С учетом уравнения (7.3) можно определить
касательное напряжение в произвольной
точке поперечного сечения вала,
определяемой радиусом ρ:
-
есть полярный момент инерции сечения.
С учетом уравнения (7.3) можно определить
касательное напряжение в произвольной
точке поперечного сечения вала,
определяемой радиусом ρ:
|
(7.6) |
а также максимальное касательное напряжение, действующее на контуре вала:
|
(7.7) |
где Wp - полярный момент сопротивления.
Эпюра распределения касательных напряжений по радиусу показана на рисунке 7.4 для сплошного и полого валов.
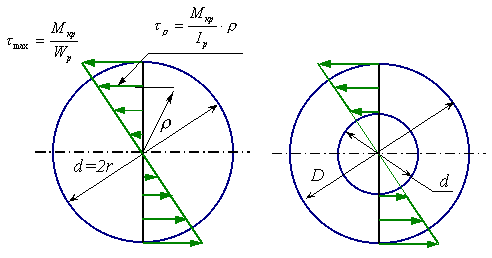
Рисунок 7.4.
Угол закручивания вала нетрудно определить на основе полученного выше уравнения:
![]() ,
,
из которого с учетом (7.6) имеем:
|
(7.8) |
Угол закручивания всего бруса
|
(7.9) |
Если брус имеет несколько участков с различными аналитическими выражениями для Мкр или различными выражениями Ip, то
|
(7.10) |
В частном случае при Мкр(x)=const или Ip=const, то есть только для бруса постоянного сечения, нагруженного по концам сосредоточенными парами,
|
(7.11) |

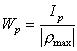 .
.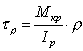 ,
,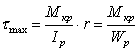 ,
,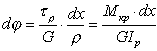 .
.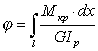 .
.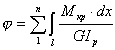 .
.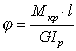 .
.