Пример 8.9

Определить прогиб середины пролета балки (рисунок 8.33).

Перемножить эпюры от заданных нагрузок и единичной силы сразу на всей длине балки нельзя, так как единичная эпюра ограничена двумя прямыми. Поэтому перемножим эпюры на половине балки и результат удвоим. Используя данные таблица 8.1, получаем

.

Нетрудно проверить, что правая часть последнего выражения имеет размерность длины.

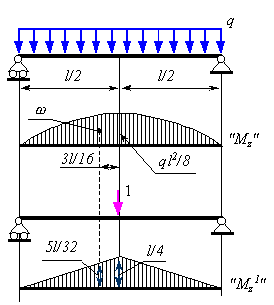
Рисунок 8.33.

Пример 8.10

Определить прогиб в точке В балки, показанной на рисунок 8.34.

Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы, приложенной в точке В. Чтобы перемножить эти эпюры, надо балку разбить на три участка, так как единичная эпюра ограничена тремя различными прямыми.

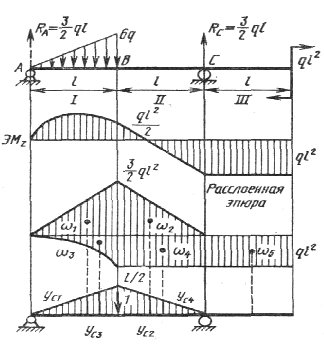
Рисунок 8.34

Операция перемножения эпюр на втором и третьем участках осуществляется просто. Затруднения возникают при вычислении площади и координат центра тяжести основной эпюры на первом участке. В таких случаях намного упрощает решение задачи построение расслоенных эпюр. При этом удобно одно из сечений принять условно за неподвижное и строить эпюры от каждой из нагрузок, приближаясь справа и слева к этому сечению. Целесообразно за неподвижное принимать сечение в месте перелома на эпюре единичных нагрузок.

Расслоенная эпюра, в которой за неподвижное принято сечение В, представлена на рисунок 8.34. Вычислив площади составных частей расслоенной эпюры и соответствующие им ординаты единичной эпюры, получаем

.

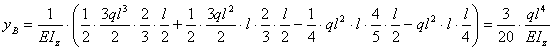Определение перемещений с помощью правила «дирижера»

Правило «дирижера» предназначено для «быстрого» вычисления интеграла Мора в случае, когда одна из перемножаемых эпюр описывается квадратичной параболой, а другая – прямолинейным законом (рисунок 8.31)

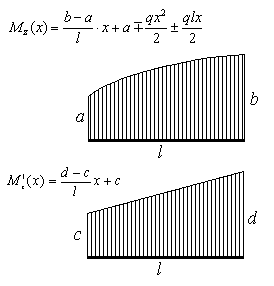
Рисунок 8.31.

Подставляя аналитические выражения для моментов под интеграл Мора, получим

,

(8.47)

где знак плюс в формуле берется, если эпюра M_z(x) - выпукла в сторону от оси эпюры и знак минус, если – вогнута (для эпюры, изображенной на рисунок 8.31 нужно ставить знак плюс). Если эпюра M_z(x) прямолинейна, то второе слагаемое в формуле (8.47) равно нулю.

8. Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности

Для определения напряженного состояния в какой-нибудь точке тела, нужно вокруг этой точки выделить элементарный параллелепипед.

По граням этого параллелепипеда, в общем случае, будут действовать нормальные и касательные, напряжения.

Зная эти напряжения, всегда можно найти главные напряжения и главные площадки. Следовательно, напряженное состояние в каждой точке тела, в конечном счете, будет определяться тремя главными напряжениями s₁, s₂, s₃.

Если из трех главных напряжений два равны нулю, то будет иметь место линейное напряженное состояние в данной точке тела.

Если из трех главных напряжений только одно равно нулю, то будет иметь место плоское напряженное состояние в данной точке тела.

Если ни одно из главных напряжений не равно нулю, то будет иметь место объемное напряженное состояние в данной точке тела.

Если во всех точках тела будет один и тот же тип напряженного состояния, то будет иметь место однородное напряженное состояние тела.

Линейное напряженное состояние называют простым напряженным состоянием, плоское и объемное напряженное состояние - сложным.

Тип напряженного состояния нельзя отождествлять с одноименным видом деформации; так при линейном напряженном состоянии могут происходить объемные деформации и т. д.
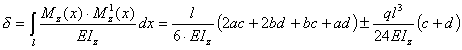