Пример 12.4

Решить раму, представленную на рисунок 12.13.

Согласно свойству обратно симметричных рам, одноименные опорные реакции равны по величине и противоположны по направлению. Следовательно, R_x=0, R_x=M/l.

Эпюра показана на рисунок 12.13.

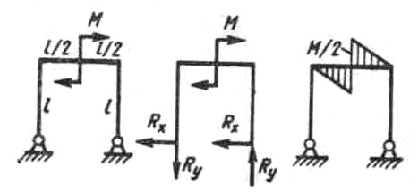
Рисунок 12.13.

Пример 12.5

Раскрыть статическую неопределимость рамы, представленной на рисунок 12.14.

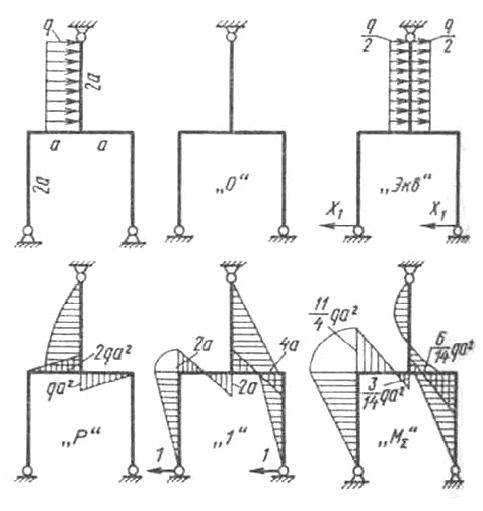
Рисунок 12.14.

Данная рама обратно симметрична. В этом нетрудно убедиться, представив распределенную нагрузку так, как показано на рисунок 12.14. Основную систему получим, сняв горизонтальные связи в нижних шарнирных опорах. В данном случае в качестве основной выбрана, вообще говоря, статически неопределимая система. Однако при обратно симметричной нагрузке опорные реакции в катковых опорах будут равны по величине и противоположны по направлению и их можно определить из уравнения равновесия.

Коэффициенты канонического уравнения δ_1P+δ₁₁X₁=0 найдем перемножением эпюр:

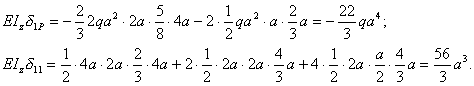
Тогда .

Суммарная эпюра представлена на рисунок 12.14.

Остановимся теперь на особенностях расчета центрально симметричных (рисунок 12.15) и центрально обратно симметричных (рисунок 12.16) рам. В первом случае при повороте одной половины рамы вокруг центра симметрии на 180° внешние силы совпадают по направлению, а во втором - окажутся противоположны по направлению.

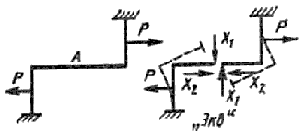
Рисунок 12.15.

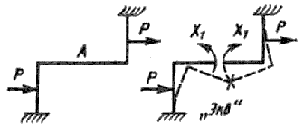
Рисунок 12.16.

Разрежем обе рамы по центру симметрии и представим себе характер деформации этих рам под действием сил P. Из рисунок 12.15 видно, что сечения рамы в месте разреза не поворачиваются друг относительно друга, а только расходятся в вертикальном и горизонтальном направлениях. Это означает, что в сечении изгибающие моменты равны нулю и действуют только нормальные X₂ и перерезывающие силы X₁.

В таких же сечениях второй рамы (см. рисунок 12.16), наоборот, должны действовать изгибающие моменты X₁ и будут отсутствовать нормальные и перерезывающие силы, так как эти сечения только поворачиваются друг относительно друга.

В центрально симметричных и обратно симметричных рамах основную систему следует выбирать удалением лишних связей в сечении по центру симметрии.

В смешанных статически неопределимых конструкциях при выборе основной системы следует сначала разрезать тяги и пружины и только после этого удалить лишние связи в элементах рамного типа.

Пример 12.6

Определить усилие в тягах и построить суммарную эпюру изгибающих моментов для рамы, представленной на рисунок 12.17, если I_z=Fa²/3.

Вследствие симметрии рамы относительно вертикальной оси усилия в тягах будут равны по величине и симметричны по направлению. Эквивалентная система и эпюры от заданной нагрузки и единичных сил показаны на рисунок 12.17.

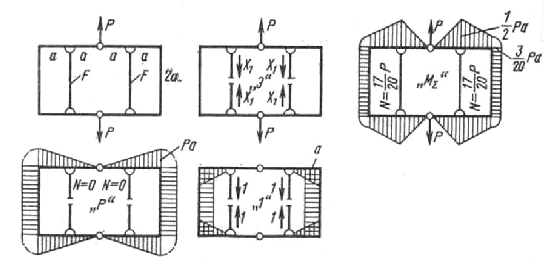
Рисунок 12.17.

Вычисляя коэффициенты канонического уравнения δ_1P+δ₁₁X₁=0 по формуле

,

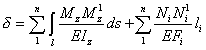получаем

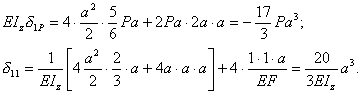
Следовательно, нормальные силы в тягах .

Суммарная эпюра приведена на рисунок 12.17. Там же приведены значения нормальных сил N в тягах.

12. Устойчивость сжатых стержней. Продольный изгиб Понятие об устойчивости первоначальной формы равновесия

Исследование причин разрушения различных сооружений показало, что для надежной работы конструкции под нагрузкой недостаточно сделать ее элементы прочными, необходимо еще обеспечить сохранение первоначальной формы равновесия как самих элементов, так и всей конструкции в целом.

Известно, что равновесие может быть устойчивым, безразличным и неустойчивым.

Равновесие называется устойчивым, если при малом отклонении от положения равновесия система возвращается в первоначальное положение, как только будет устранена причина, вызывающая это отклонение; равновесие называется неустойчивым, если система не возвращается в исходное положение, а отклоняется от него еще больше; равновесие называется безразличным, если новое положение системы после отклонения от исходного остается положением равновесия и после удаления внешнего воздействия.

Эти три формы равновесия можно проиллюстрировать примерами положения шарика на дне чаши, на выпуклой поверхности и на горизонтальной плоскости (рисунок 13.1). В первом случае исходное положение шарика является устойчивым, так как при малых отклонениях он возвратится в первоначальное положение, как только будет устранена причина, вызвавшая отклонение. Во втором случае исходное положение шарика может служить примером неустойчивого равновесия, а в третьем - безразличного.

Рисунок 13.1	Рисунок 13.2

Речь идет о малых отклонениях потому, что устойчивое равновесие при малых отклонениях может стать неустойчивым при больших отклонениях от исходного положения. Примером тому может служить положение шарика на поверхности, представленной на рисунок 13.2. При больших отклонениях шарик, очевидно, не будет возвращаться, а при малых отклонениях будет возвращаться в первоначальное положение.

Сказанное относится и к упругим телам. Однако характер равновесия упругих тел существенно зависит от величины действующих на них сил. Например, прямолинейная форма равновесия длинного прямого стержня, подвергнутого осевому сжатию силой Р (рисунок 13.3, а), устойчива только до определенного значения сжимающей силы. Если такой стержень при малых значениях силы Р несколько отклонить от исходного положения, то при устранении причин, вызывающих это отклонение, он снова примет первоначальную прямолинейную форму.

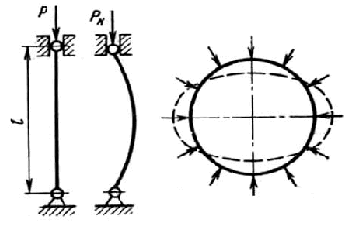
Рисунок 13.3.

Однако при возрастании силы Р стержень все медленнее и медленнее будет возвращаться к своей первоначальной прямолинейной форме, и, наконец, при некотором значении силы Р, называемом критическим, стержень не распрямится, а сохранит ту форму, которую ему придали (предполагаются малые отклонения стержня от прямолинейной формы). Таким образом, при значении силы Р, равном критическому (P=P_k), стержень будет находиться в условиях безразличного равновесия.

Если сила Р превысит критическое значение, прямолинейная форма равновесия станет неустойчивой.

Практически изгиб стержня начинается раньше, чем сила Р достигает критического значения. Это объясняется неоднородностью материала, начальным искривлением (прогибом) оси реального стержня и некоторым эксцентриситетом в приложении нагрузки. Однако прогибы реального стержня начинают быстро расти и становятся опасными только при приближении сжимающей силы к критическому значению.

Описанное явление изгиба стержня продольной силой называется продольным изгибом.

Аналогичные явления наблюдаются в различных упругих системах, содержащих гибкие сжатые части, тонкие пластинки и оболочки. Так, например, при сжатии кругового тонкостенного кольца равномерно распределенными радиальными нагрузками происходит изменение его первоначальной круговой формы, как только интенсивность сжимающей нагрузки достигает критического значения (рисунок 13.3, б).

В практических расчетах на устойчивость критическую нагрузку считают разрушающей и допускаемую нагрузку определяют как часть критической:

,

(13.1)

где n_y - коэффициент запаса устойчивости.

Величина коэффициента запаса устойчивости принимается примерно равной запасу прочности. Например, для стали принимают n_y=2÷4 в зависимости от условий работы конструкции, а для неоднородных материалов запас устойчивости значительно увеличивают.

Следует иметь в виду, что потеря устойчивости может произойти при напряжениях, значительно меньших допускаемых напряжений, принятых для расчета на прочность.

Из многочисленного ряда задач в области устойчивости упругих систем мы рассмотрим только задачу об устойчивости сжатых стержней.