Принципы сопротивления материалов Принцип Сен-Венана

Методика схематизации системы внешних сил регулируется принципом Сен-Венана, который формулируется следующим образом: если совокупность некоторых сил, приложенных к небольшой части поверхности тела, заменить статически эквивалентной системой других сил, то такая замена не вызовет существенных изменений в условиях нагружения частей тела, достаточно удаленных от мест приложения исходной системы сил.

Принятие этого принципа означает условие рассматривать только те части тела, которые достаточно удалены от места приложения нагрузки. Расчетом деталей в местах их контакта занимается самостоятельная научная дисциплина – математическая теория упругости. На рисунок 1.7 представлена иллюстрация принципа Сен-Венана на простейшем примере. Из рисунка видно, что замена распределенной нагрузки статически эквивалентной сосредоточенной силой не окажет существенного влияния на условия нагружения части бруса, удаленной на расстояние не менее 3...5·t от правой границы действия распределенной нагрузки, где t - наибольший размер поперечного сечения бруса.

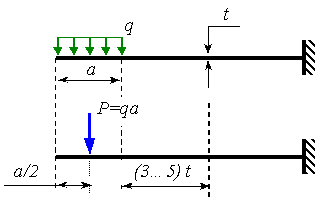
Рисунок 1.7. Иллюстрация принципа Сен-Венана

Принцип независимости действия сил

При действии на относительно жесткое тело несколько сил, результат действия одной части этих сил не зависит от результата действия остальных сил.

Следствие 1. Результат действия на тело нескольких сил равен сумме результатов отдельного действия каждой силы.

Следствие 2. Результат действия на тело нескольких сил не зависит от последовательности приложения этих сил.

Принцип начальных размеров

При составлении условий равновесия реального тела оно может считаться абслютно твердым.

В действительности при нагружении форма и размеры тела меняются, поэтому точки приложения сил и линии их действия тоже меняются; учет этих изменений дает поправку в четвертом-пятом знаках численного результата, что несущественно.

1. Внутренние силы. Метод сечений

Нагрузки, приложенные к одной какой-нибудь части тела, от точки к точке передаются остальным частям тела. Силы взаимодействия между частями тела, вызванные нагрузками, называются внутренними силами. В первую очередь, из-за простоты, изучают внутренние силы, распределенные по плоским, сечениям тела. При этом используют метод сечений, заключающийся в следующем. Пусть на тело АВ действует уравновешенная система сил (рисунок 2.1). Через это тело мысленно проводится плоское сечение «F», которое делит тело на части A и B. В каждом таком сечении будут действовать внутренние силы, характеризующие взаимодействие частей A и B тела. Отбросим одну часть тела, например B, и заменим ее действие на оставшуюся часть силами, распределенными по сечению F. Обнажая эту поверхность, мы переводим внутренние силы в разряд внешних, благодаря чему появляется возможность использования положений статики твердого тела. Пользуясь этим, приведем внутренние силы, распределенные по сечению к главному вектору и главному моменту в центре тяжести сечения. Их можно разложить на компоненты вдоль осей координат. Следовательно, в общем случае внутренние силы могут иметь шесть компонентов - R_x, R_y, R_z, M_x, M_y, M_z (рисунок 2.1). Величина компонентов внутренних сил может быть найдена из шести условий равновесия оставленной части тела:

При определении составляющих внутренних сил могут возникать как статически определимые, так и статически неопределимые задачи. В статически неопределимых задачах в дополнение к условиям равновесия составляют условия совместности деформаций сторон сечения «F» (при совмещении деформированные поверхности сечения «F» должны совпадать).

В процессе удовлетворения уравнениям равновесия и условиям совместности деформаций, между компонентами внутренних сил и внешними силами устанавливается функциональная зависимость, в которой находят свое отражение форма и размеры тела, расположение сечения «F», направление и место приложения нагрузочных сил, механические свойства материала. Каждой компоненте внутренних сил соответствует свой вид деформации: R_x соответствует растяжение или сжатие, R_y и R_z - сдвиг в направлении осей y и z, M_x - кручение, M_y и M_z - изгиб относительно осей y и z. Каждая компонента характеризует сопротивление тела какому-нибудь одному виду деформации. При наличии только одной какой-нибудь компоненты внутренних сил будет иметь место простое сопротивление тела. При наличии двух и более компонентов будет сложное сопротивление тела.

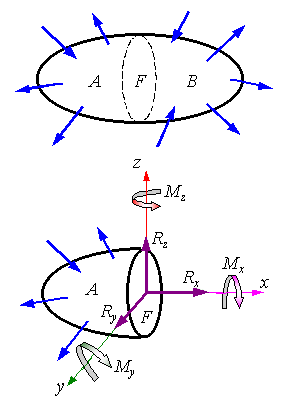
Рисунок 2.1. Иллюстрация метода сечений