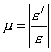ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Бийский технологический институт (филиал)
государственного образовательного учреждения высшего профессионального образования
«Алтайский государственный технический университет им. И .И. Ползунова»
д.т.н., профессор кафедры ТМ Анисимов И.И.
С о п р о т и в л е н и е м а т е р и а л о в
(Часть 1 и 2)
К о н с п е к т л е к ц и й
(III и IV семестр)
170104.65 – Высокоэнергетические устройства
автоматических систем
160302.65 - Ракетные двигатели
Факультет механический
Кафедра Техническая механика
2010 год
Оглавление
2
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ 2
Введение 3
1. Внутренние силы. Метод сечений 11
2. Напряжения и деформации 13
3. Растяжение-сжатие 32
4. Сдвиг (срез) 60
5. Геометрические характеристики плоских сечений 67
6. Кручение 78
7. Плоский прямой поперечный изгиб 101
8. Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности 140
9. Расчет на прочность при сложном сопротивлении 151
10. Перемещения в пространственном брусе малой кривизны при произвольной нагрузке 169
11. Статически неопределимые стержневые системы 173
12. Устойчивость сжатых стержней. Продольный изгиб 194
13. Расчет элементов конструкций, движущихся с ускорением 213
14. Расчет на прочность при ударном действии нагрузок 225
Введение
Сопротивление материалов является частью более общей науки – механики твердого деформируемого тела, в которую входят: теория упругости, теории пластичности и ползучести, теория сооружений, строительная механика, механика разрушения и др.
Задачей науки о сопротивлении материалов является изучение методов расчета элементов конструкций и деталей машин на прочность, жесткость и устойчивость.
Прочностью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил, не разрушаясь.
Жесткостью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил, получая лишь малые упругие деформации.
Устойчивостью называется способность элемента конструкции сохранять первоначальную форму равновесия под действием приложенных сил.
Реальные тела не являются абсолютно твердыми и под действием приложенных к ним сил изменяют свою первоначальную форму и размеры, то есть деформируются. Деформации тела, исчезающие после снятия внешних сил, называются упругими, а не исчезающие – остаточными или пластическими деформциями.
Определение размеров деталей или внешних нагрузок, при которых исключается возможность разрушения деталей, является целью расчета на прочность.
Определение размеров деталей или внешних нагрузок, при которых исключается возможность появления недопустимых с точки зрения нормальной работы конструкции деформаций этих деталей, является целью расчета на жесткость.
Реальный объект и расчетная схема
Реальный объект, освобожденный от несущественных особенностей, не влияющих заметным образом на работу системы в целом, называется расчетной схемой. Переход от реального объекта к расчетной схеме осуществляется путем схематизации свойств материала, системы приложенных сил, геометрии реального объекта, типов опорных устройств и т.д.
Схематизация свойств материала
Реальные материалы обладают разнообразными физическими свойствами и характерной для каждого из них структурой. С целью упрощения расчетов в сопротивлении материалов используются следующие допущения о свойствах материала.
1. Материал считается однородным, то есть его свойства во всех точках одинаковы.
2. Материал считается изотропным, то есть его свойства во всех направлениях одинаковы.
Изотропными являются аморфные материалы, такие как стекло и смолы. Анизотропными являются пластмассы, текстолит и т.п. Металлы являются поликристаллическими телами, состоящими из большого количества зерен, размеры которых очень малы (порядка 0,01 мм). Каждое зерно является анизотропным, но вследствие малых размеров зерен и беспорядочного их расположения металлы проявляют свойство изотропии.
3. Материал обладает свойством идеальной упругости, вследствие которой деформируемое тело полностью восстанавливает свою форму и размеры после снятия нагрузки независимо от величин нагрузок и температуры тела.
4. Форма и размеры упругого тела меняются прямо пропорционально изменению нагрузок, то есть по известному закону Гука (1660 г.).
В случае чистого однородного растяжения или сжатия призматического стержня, закон Гука имеет вид:
|
(1.1) |
,где P - растягивающая (сжимающая) осевая сила; lo, Fo - исходная длина и исходная площадь поперечного сечения стержня; E - физическая константа материала – модуль продольной упругости, различный для разных материалов; Δl - абсолютное удлинение расчетной части lo стержня. Формулу (1.1) можно представить в виде:
|
(1.2) |
или
|
(1.3) |
и
|
(1.4) |
,где ε = Δl/lo - относительное удлинение расчетной части стержня; σ = P/Fo - нормальное напряжение, то есть усилие, приходящееся на единицу площади Fo поперечного сечения стержня.
В формулировке данной гипотезы границы применения закона пропорциональности Гука ничем не оговариваются, хотя в действительности при некоторых нагрузках начинается существенное отклонение от закона пропорциональности.
В пределах упругости имеет место эффект Пуассона (1816 г.) – отношение относительных поперечных удлинений ε/ к относительным продольным удлинениям ε есть величина постоянная для данного материала»:
|
(1.5) |
или
|
(1.6) |
,где μ - коэффициент Пуассона – упругая константа материалов (0<μ<0.5). Уравнение (1.6) выражает закон Гука для поперечных деформаций.
5. Материал обладает свойством сплошности, то есть способностью сплошь (без пустот) заполнять пространство, ограниченное поверхностью тела. Вследствие этого материал считается непрерывным, что позволяет использовать для определения напряжений и деформаций математический аппарат дифференциального и интегрального исчисления.
6. Упругие тела являются относительно жесткими, благодаря чему перемещения точек тела весьма малы по сравнению с размерами самого тела. Эта гипотеза служит основанием для принципа начальных размеров.
Схематизация геометрии реального объекта
Схематизация геометрии объекта в сопротивлении материалов сводится к рассмотрению бруса, оболочки и массива.
Брусом называется тело, два измерения которого малы по сравнению с третьим (рисунок 1.1).
Рисунок 1.1. Брус
Оболочкой называется тело, одно измерение которого мало по сравнению с двумя другими (рисунок 1.2).
Рисунок 1.2. Оболочка
Массивом называется тело, все три измерения которого мало отличаются друг от друга (рисунок 1.3).
Рисунок 1.3. Массив
Схематизация опорных устройств
Пространственное твердое тело имеет шесть степеней свободы перемещений - три поступательных движения и три вращательных вокруг трех взаимно перпендикулярных осей. Плоское тело имеет только три степени свободы — два поступательных движения в направлении двух осей и вращение вокруг третьей оси. Опорные устройства препятствуют тем или иным из указанных перемещений тела или вообще исключают всякое его движение. Опорные устройства классифицируются по числу связей, накладываемых на перемещения опорных точек (узлов) тела. Связь обычно представляют в виде стержня, соединяющего тело с опорной поверхностью. Если нет специального указания, опорные связи и поверхности считаются абсолютно жесткими.
При нагружении тела на него со стороны опорных связей начинают действовать силы, называемые опорными реакциями. Опорные реакции находятся из уравнений равновесия тела, у которого опорные связи мысленно удалены и заменены силами, направленными вдоль снятых связей.
Для плоского тела, и в частности для плоского бруса, основными видами опор являются шарнирно-подвижная, шарнирно-неподвижная и защемляющая неподвижная.
Шарнирно-подвижная, или, иначе, катковая опора исключает перемещение опорного узла А в направлении, перпендикулярном опорной поверхности, но не препятствует вращению тела вокруг опорной точки и поступательному перемещению параллельно опорной поверхности. Такой опоре соответствует одна опорная реакция, направленная перпендикулярно опорной поверхности. Схематические изображения катковой опоры представлены на рисунок 1.3. Там же показано направление опорной реакции.
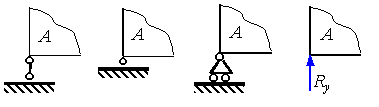
Рисунок 1.3. Шарнирно-подвижная опора
Шарнирно-неподвижная, или, короче, шарнирная опора исключает всякое поступательное движение опорного узла A, но не препятствует вращению тела вокруг опорной точки. Реакцию такой опоры, направление которой заранее неизвестно, принято раскладывать на две составляющие Rx и Ry, направленные по касательной и нормали к опорной поверхности, как показано на рисунок 1.4. На этом же рисунке представлены схематические изображения шарнирных опор.
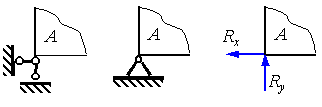
Рисунок 1.4. Шарнирно-неподвижная опора
Защемляющая неподвижная опора, или, иначе, заделка (рисунок 1.5) исключает поступательные и вращательные движения тела. В соответствии с тремя связями, накладываемыми на тело, реакциями заделки являются силы Rx и Ry и опорный момент M. Конструктивное оформление опорных устройств каждого из указанных типов отличается большим разнообразием. В приведенных на рисунок 1.3, 1.4 и 1.5 общепринятых схематических изображениях опор подчеркиваются их самые характерные особенности.
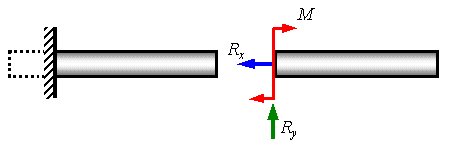
Рисунок 1.5. Неподвижная опора
Схематизация системы внешних сил
Внешние силы, воспринимаемые конструкциями и их деталями называются нагрузками. К внешним силам относят также и реакции связей. Внешние силы могут быть сосредоточенными и распределенными, объемными и поверхностными, статическими и динамическими. Под сосредоточенными силами подразумевают давления, распределенные по небольшой части поверхности тела, а не сосредоточенные в одной точке. К объемным относятся силы тяжести, силы магнитного притяжения, инерционные силы и т.д. Объемные силы непрерывно распределены по всему телу. Поверхностные силы являются результатом взаимодействия твердых тел или воздействия на них внешней среды, например потока воздуха на крыло самолета. Поверхностные силы распределены по поверхности тела.
Статические силы изменяются столь медленно и плавно, что возникающими при этом ускорениями движущихся масс можно пренебречь. При статическом нагружении можно считать, что нагрузки во всех точках тела воспринимаются одновременно. При динамическом нагружении возникают значительные инерционные силы, которые нужно учитывать наряду с другими нагрузками.
В сопротивлении материалов изучают действие только уравновешенных систем внешних и внутренних сил. Поэтому при рассмотрении вопросов равновесия деформируемого тела применимы все законы статики и динамики твердого тела. Можно перемещать силы вдоль линии их действия, заменять системы сил статически эквивалентными системами и т.д. При определении деформаций, энергий деформаций и других величин, связанных с перемещениями, указанные действия производить нельзя.
Рассмотрим методику схематизации системы внешних сил, действующих на тело на примере бруса с прямолинейной осью (рисунок 1.6). Вместо бруса изображается его ось, представляющая собой геометрическое место центров тяжестей поперечных сечений. Все действующие на брус нагрузки сводятся к оси. При этом нагрузки, приложенные к участкам небольших размеров по сравнению с размерами бруса, заменяются сосредоточенными силами. В противном случае нагрузка остается распределенной по линии. При переносе сил в направлении перпендикулярном их линиям действия возникают сосредоточенные моменты.
Сосредоточенные силы P измеряются в ньютонах [Н], сосредоточенные моменты M имеют размерность [Нм], интенсивность распределенной по линии нагрузки q измеряется в [Н/м].
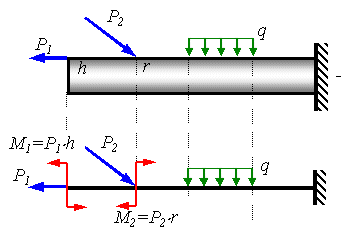
Рисунок 1.6. Схематизация системы приложенных сил