§ 6. Дисконтирование по простым процентам

6.1. Сущность дисконтирования

В условиях рынка кредит выступает в различных формах. Основными являются коммерческий и банковский кредиты.

Коммерческий кредит заключается в предоставлении товаров и услуг одним субъектом сделки другому с оплатой за них через определенное время, то есть происходит отсрочка уплаты денег за проданные товары и услуги. Распространенным инструментом такого кредита является коммерческий вексель. Вексель - это особый вид письменного долгового обязательства, который дает его владельцу бесспорное право требовать уплаты денег с должника по истечении указанного на векселе срока.

Векселя бывают простые и переводные. Простой вексель - это долговое обязательство, выданное заемщиком на имя кредитора и содержащее указание места и времени выдачи векселя, его суммы, места и времени платежа и наименование лица, которому заемщик обязан произвести платеж. Переводной вексель или тратта представляет собой письменный приказ одного лица (кредитора) другому лицу (заемщику) об уплате третьему лицу суммы, обозначенной на векселе.

Банковский кредит - это кредит, предоставляемый одним субъектом сделки другому в виде денежной ссуды. Механизм оформления такого кредита может предусматривать различные варианты, в т.ч. и выписку заемщиком ссуды векселей на имя кредитора.

Кредитор (векселедержатель) в случае необходимости получения денег по векселю или по другим долговым обязательствам ранее указанных в нем сроков, может продать этот вексель другому банку или субъекту по цене, ниже номинальной стоимости векселя. Такая сделка называется учетом векселя или дисконтированием.

Дисконтом (D) называется разность между номинальной стоимостью (S) долгового обязательства и суммой (Р) , полученной векселедержателем в результате учета векселя, т.е.

Термин дисконтирование употребляется и в более широком смысле - как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Другими словами, дисконтирование - это способ нахождения величины Р на некоторый момент времени при условии, что в будущем, при начислении на нее процентов, она могла бы составить наращенную сумму S.

Величину Р, найденную с помощью дисконтирования наращенной суммы S, называют современной величиной суммы S или современной (текущей) стоимостью суммы S.

Современная величина (стоимость) Р является одним из важнейших понятий в количественном анализе финансовых операций. В частности, это понятие позволяет сравнивать между собой различные (по срокам платежа) финансовые контракты.

В зависимости от вида процентной ставки применяются два метода дисконтирования - математическое и банковское (банковский или коммерческий учет).

6.2. Математическое дисконтирование

Математическое дисконтирование представляет собой решение задачи, обратной определению наращенной суммы. Задача при этом формулируется следующим образом: какую сумму P следует выдать в долг на n лет, чтобы получить в конце срока ссуды сумму S, при условии, что на долг начисляется i% годовых.

Тогда, решив уравнение относительно Р, получаем:

(13)

где дробь называется дисконтным множителем.

Установленная по формуле (3) сумма Р и является современной величиной суммы S, которая будет выплачена через n лет.

№ 11. Через один год владелец векселя, выданного коммерческим банком, должен получить по нему 280 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если его доходность должна составить 40% годовых.

Решение. Найдем современную стоимость

тыс. руб.

№ 12. Владелец векселя (№ 11) предъявил его банку для учета за два месяца до даты погашения. Определить дисконтированную величину, то есть сумму, полученную владельцем векселя, и величину дисконта.

Решение:

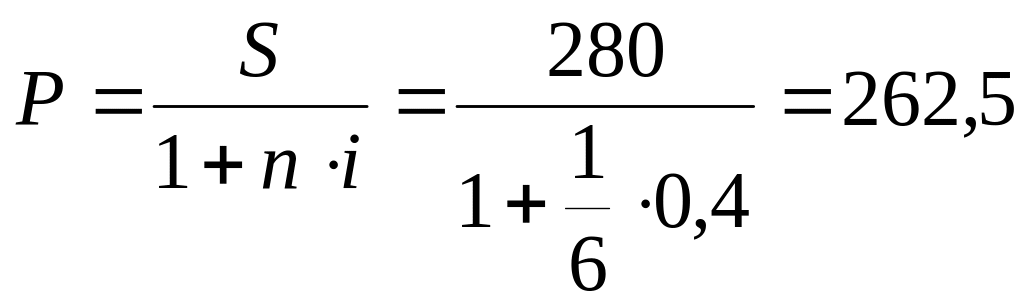тыс. руб. –

сумма, полученная владельцем векселя в результате его учета.

Дисконт (доход банка) равен

тыс. руб.

На практике банк обязательно установит для учета ставку более высокую, чем приведена в примере, с целью получения большего дисконта, например 50%. Тогда сумма, полученная владельцем векселя, составит

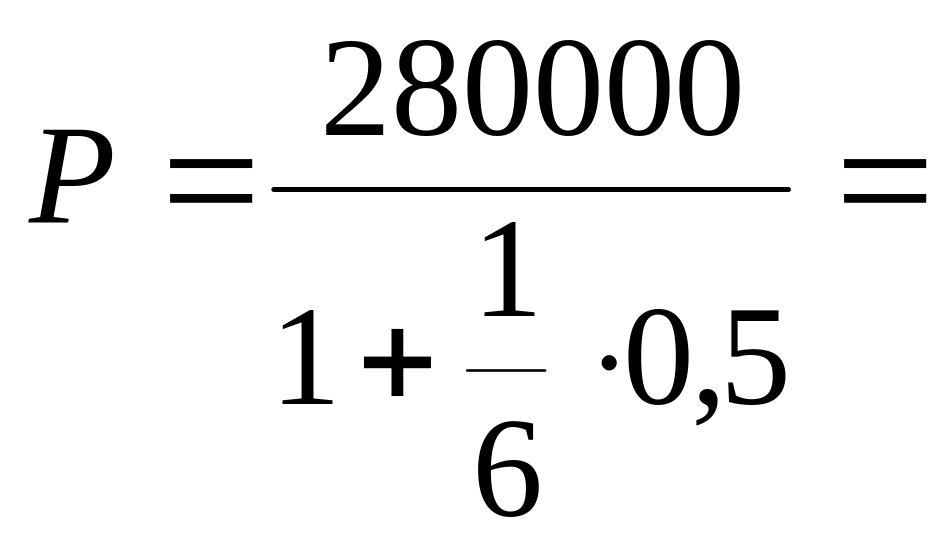258461 руб. 54 коп.,

а дисконт (доход банка) будет равен

21538 руб. 46 коп.

Используя приведенные выше формулы, можно рассчитать величину эффективной годовой процентной ставки, которая отражает реальный доход владельца векселя.

Так как , то

или (14)

№ 13. Определить эффективную процентную ставку владельца векселя из № 12.

Решение. Здесь К = 360 или 365 (366) дней, t =360 – 60 = 300 дней. Тогда эффективная ставка равна:

Таким образом, владельцу векселя, чтобы получить 258.461 руб. 54 коп. через 300 дней необходимо вложить в банк 200.000 руб. по ставке 35,08% годовых.