§ 5. Потребительский кредит

Потребительский кредит предоставляется населению для покупки предметов личного потребления. Существуют различные формы потреби-тельского кредита, которые отличаются друг от друга методами и сроками погашения (возврата):

1. Потребительский кредит может быть предоставлен с отсрочкой платежа и последующим разовым погашением всей суммы, включающей и процентные платежи.

2. Кредит может погашаться в рассрочку по частям:

а) проценты начисляются на всю сумму кредита, а сумма задолженности погашается равномерно равными выплатами на протяжении всего срока кредита;

б) суммы процентных платежей изменяются от одного периода платежа к другому, а сумма основного долга погашается равномерно.

Существуют и другие способы погашения кредита.

5.1. Погашение потребительского кредита разовой выплатой

В этом случае наращенная сумма долга, подлежащая погашению, равна:

(8)

где Р – сумма потребительского кредита, – срок кредита (в годах), – процентная ставка.

5.2. Погашение потребительского кредита равными выплатами

В этом случае величина разовой выплаты составит:

(9)

где – число погасительных платежей в году.

Отметим, что в этом случае, несмотря на уменьшение величины долга с каждым платежом, фактическая процентная ставка окажется значительно выше ставки в %.

5.3. Погашение потребительского кредита

изменяющимися суммами

В этом случае процентный платеж может рассчитываться например следующим образом: для первого периода процентный платеж рассчитывается на всю величину долга; для второго и последующего периодов – рассчитывается уже на оставшуюся, после предыдущих выплат, часть долга. Сам же основной долг выплачивается равными взносами.

Пусть кредит на сумму ден. ед, выдан на лет под % годовых (ставка выражается десятичной дробью) и должен погашаться раз в год изменяющимися платежами. Тогда выплата основного долга за каждый период равна

а процентные платежи будут вычисляться по формулам:

а) для первого периода

б) для второго месяца

в) для k-го месяца

г) для -го месяца

(10)

Следовательно, общая величина процентных выплат за предоставленный кредит равна

(11)

Здесь множитель называют процентным коэффициентом. Он показывает соотношение между величиной процентных выплат и вели-чиной кредита.

В этом случае общая сумма, возвращенная за пользование кредитом, составит

(12)

№ 10. Предоставлен потребительский кредит в размере 1800 руб. на покупку телевизора сроком на 6 месяцев под 12% годовых. Составить план погашения кредита.

Решение.

1. Разовая выплата с отсрочкой платежа:

руб.

– через 6 месяцев после получения кредита, где сумма процентных платежей равна 108 руб.

1. Погашение кредита равными ежемесячными выплатами: по

руб.

каждый месяц, шесть раз.

3. Погашение кредита изменяющимися суммами.

В этом случае разовые выплаты основного долга составляют:

руб.

каждый месяц.

Процентные платежи:

а) за первый месяц –

руб.;

б) за второй месяц –

руб.;

в) за остальные месяцы –

руб., руб.

руб., руб.

Тогда сумма процентных платежей за пользование кредитом равна:

руб.,

или

руб.

И общая сумма погашения кредита составит

руб.

План погашения кредита удобно представить в виде таблицы (в руб.)

Таблица 1

Месяц	Долг	Процентные платежи	Выплата основного. долга	Месячный взнос
1	1800	18	300	318
2	1500	15	300	315
3	1200	12	300	312
4	900	9	300	309
5	600	6	300	306
6	300	3	300	303
итого:		63	1800	1863

Очевидно, что для кредитора выгоднее второй вариант, а для должника третий вариант погашения долга.

Графически план погашения потребительского кредита (да и любого кредита, погашаемого единовременно или по частям) можно изобразить в виде замкнутого контура финансовой операции:

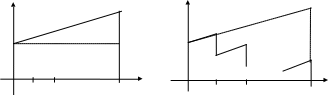S S

S S

P P

Y

Y . . .

Y

0 1 2 . . . . р t 0 1 2 . р t

для § 5.1. для § 5.2.

S

I₁

P R

I₂

R

. . . I_p

R

0 1 2 . . . р-1 р t

для § 5.3.