§ 1. Ренты с постоянным абсолютным изменением платежей

В этом случае члены ренты изменяются таким образом, что каждый последующий платеж отличается от предыдущего на одну и ту же постоянную величину , то есть члены ренты изменяются по закону арифметической прогрессии. А именно, если рента выплачивается лет (постнумерандо), получаем следующую последовательность членов ренты:

, , , ..., ,

и наращенная сумма такой ренты

. (1)

Преобразуем формулу (3):

,

где

.

Умножим на и вычислим

Следовательно,

.

Окончательно получаем

. (2)

Если члены ренты уменьшаются на величину , то

. (3)

Для рент пренумерандо, когда платежи вносятся вначале периодов

. (4)

Для нахождения современной стоимости такой ренты воспользуемся равенством , откуда

. (5)

Для определения размера первого платежа при заданном значении прироста , процентной ставки и наращенной суммы используем формулу (4):

, (6)

а величина прироста может быть вычислена как (из (4)):

. (7)

№ 87. Фирма получила кредит в 5 млн. руб., который должен быть погашен в течение 5 лет платежами, постоянно возрастающими на 200 тыс. руб. Платежи и начисление процентов (12% годовых) на них производятся в конце года. Определить размер первого платежа и общую сумму выплат.

Решение. Так как млн. руб., тыс. руб., , лет, то из формулы (8) вычислим :

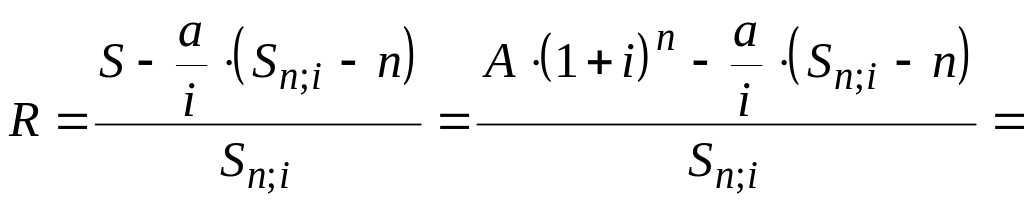
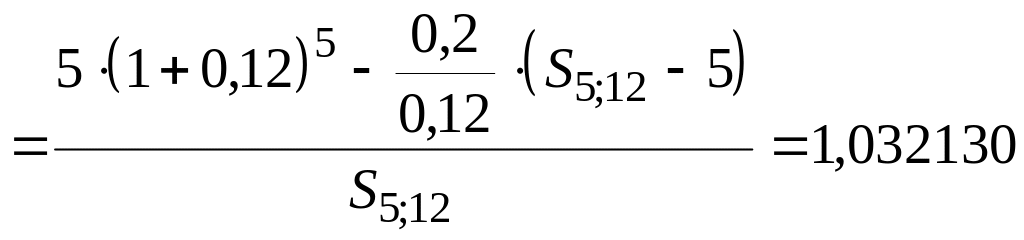(млн. руб.).

Вычислим по формуле (4):

(млн. руб.).

Проверим вычисления по формуле

(млн. руб.).

§ 2. Ренты с постоянным относительным изменением платежей

В этом случае члены ренты изменяются таким образом, что каждый последующий платеж больше предыдущего в раз. Тогда получаем за ( лет) следующую последовательность платежей:

, , , ..., ,

и наращенная сумма ренты будет вычисляться как

.

Вычислив , получим

. (8)

Современная стоимость такой ренты равна:

. (9)

№ 88. В условиях № 87 платежи увеличиваются каждый год на 20%. Определить размер первого платежа и общую сумму выплат.

Решение. Так как , то из (11) можем получить

млн, руб.

Вычислим наращенную сумму

(млн. руб.).

Расхождение с результатом № 88 вызвано ошибками округления.

Для рент пренумерандо получим:

. (10)

Некоторый практический интерес представляет соотношение эквивалентности между абсолютным ( ) и относительным ( ) приростами членов ренты. Если приравнять современные стоимости обеих видов рент

,

можно получить уравнение

,

решив которое относительно или , можно найти соответствующие зависимости между ними, например,

. (11)

Вычисление же через приводит к необходимости решения уравнения -го порядка, для чего требуются знания методов вычислительной математики.