7.4.3. Общий случай замены ренты
Если замене подлежит не один , а несколько параметров ренты, то при определении параметров новой ренты исходят из формулы
,
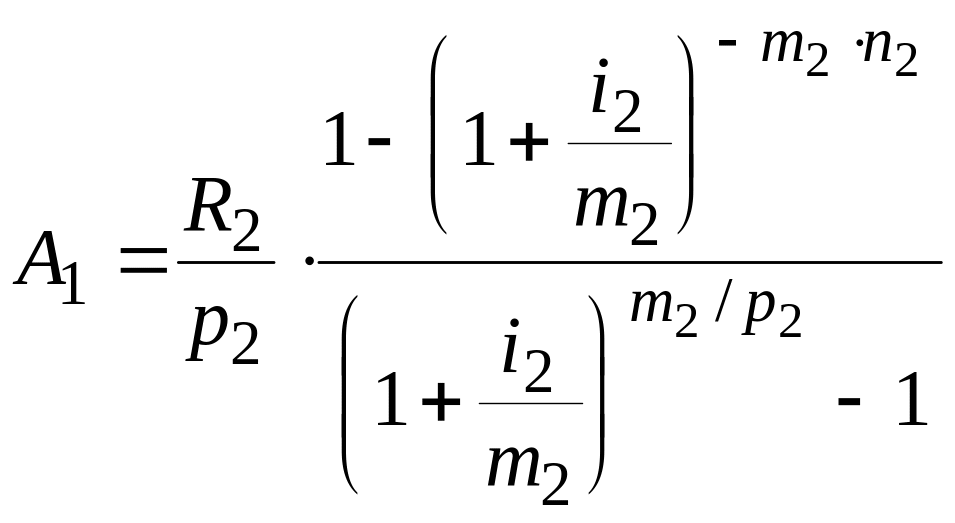где
– современная стоимость старой ренты.
Тогда, например член новой ренты
определяется из условия
.
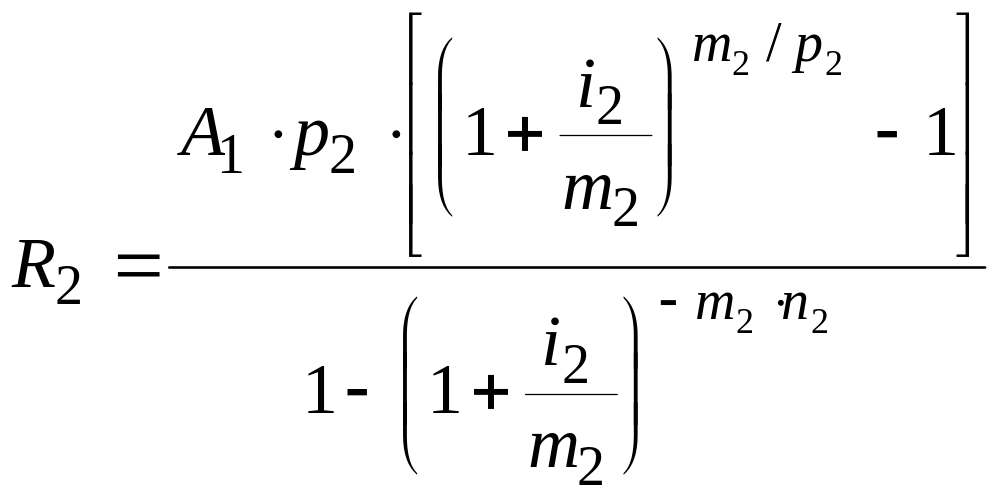(51)
№ 85. Продавец продает здание стоимостью 100 млн. руб. на следующих условиях: ежегодные платежи, вносимые в конце года, срок погашения 5 лет, годовая процентная ставка 14%. Покупатель предложил свои условия: платежи производятся два раза в год, срок выплаты – 6 лет. Определить величину рентного платежа в условиях, предложенных продавцом и покупателем.
Решение. Вычислим рентный платеж, предложенный продавцом:
руб.
Годовой платеж, предложенный покупателем
(
,
,
):
руб.
А разовый (полугодовой) платеж равен:
руб.
7.5. Консолидация рент
Консолидация рент – это объединение нескольких рент в одну, основанное на принципе финансовой эквивалентности. То есть современная стоимость консолидированной ренты должна равняться сумме консолидированных величин объединяемых рент:
,
(52)
где
– современная величина консолидированной
ренты;
– современная стоимость
-ой
заменяемой ренты,
.
Объединяемые ренты могут быть любыми: немедленными, отсроченными, -срочными и т.д. Вид и параметры консолидированной ренты должны быть определены однозначно, кроме одного параметра, который определяется из условия (52).
Например, если заданы и , то член консолидированной ренты определяется по формуле
.
(53)
Если же член консолидированной ренты задан, то срок новой ренты можно определить из условия
.
(54)
А если известно, что
,
то есть член новой ренты равен сумме
членов заменяемых рент, то
,
(55)
где
– сроки заменяемых рент,
– процентная ставка, одинаковая для
всех рент.
При объединении рент могут быть предложены и другие условия, что приводит к необходимости вывода новых формул для расчета параметров ренты. Вывод таких формул также основан на принципе финансовой эквивалентности.
№ 86. Три ренты постнумерандо
немедленные, годовые заменяются одной
отложенной на три года рентой постнумерандо.
Характеристики заменяемых рент:
,
,
тыс. руб., сроки этих рент
,
,
лет. Найти размер члена заменяющей ренты
со сроком
лет (включая отсрочку), если применяется
ставка сложных процентов, равная 20%.
Решение. Найдем сумму современных стоимостей заменяемых рент.
(тыс. руб.).
Вычислим член консолидированной ренты
(тыс. руб.).
Если бы заменяющая рента была немедленной
(
лет), то
(тыс. руб.).
Если бы был задан не срок консолидированной
ренты, а сумма годового платежа, например,
,
то срок этой ренты определим по формуле
(54), вычислив сначала ее современную
стоимость
,
тогда
года.
Следовательно,
или
,
с соответствующей компенсацией долга
(
)
или излишка (
).
Г Л А В А V
П Е Р Е М Е Н Н Ы Е П О Т О К И П Л А Т Е Ж Е Й
В предыдущей главе мы рассмотрели потоки платежей, в которых члены потока были постоянными величинами. Однако на практике бывают случаи, когда члены потока платежей изменяются по своей величине течение срока ренты. Такие изменения могут быть связаны с какими-либо обстоятельствами объективного характера (например, условиями производства и сбыта продукции и т.д.), а иногда и случайными факторами.
Поток последовательных платежей, члены которого не являются постоянными величинами, называется переменной рентой. Изменение величины последовательных платежей в ряде случаев может быть описано каким-либо законом. В других же случаях их изменение происходит без всяких видимых закономерностей, и такая последовательность платежей называется нерегулярным потоком платежей.