4. Ренты с платежами в середине периодов

Важным частным случаем постоянных рент является рента с платежами в середине периодов. Например, когда поступления от производственных инвестиций распределяются более или менее равномерно, применение рент постнумерандо или пренумерандо для описания таких потоков может привести к существенным смещениям в значении получаемых показателей (см., например, № 76). В таких ситуациях для уменьшения погрешности можно рекомендовать отнести суммы поступлений на период к середине периодов.

Тогда расчет обобщающих показателей (наращения или современной стоимости) производится путем умножения соответствующего показателя ренты постнумерандо на множитель наращения за половину периода:

, и т.д.

§ 6. Постоянная непрерывная рента

6.1. Наращенная сумма и современная стоимость

Рассмотрим ренту, в которой платежи производятся так часто, что можно считать, что они поступают непрерывно, а не дискретно, как было в ранее рассмотренных рентах. Так, отдача от инвестиций может происходить так часто, что этот поток поступлений рассматривается как непрерывный.

Выведем формулы для вычисления наращенной суммы и современной стоимости непрерывной ренты при начислении процентов один раз в год.

Учитывая, что у непрерывной ренты , имеем:

Вычислим предварительно предел:

Таким образом,

(38)

Аналогично получаем

(39)

Здесь

множитель наращения непрерывной ренты, а

множитель приведения непрерывной ренты.

Сравнение этих коэффициентов с соответствующими коэффициентами и - срочной ренты:

показывает, что при переходе от дискретной ренты постнумерандо к соответствующей непрерывной ренте соответствующие множители наращения и приведения увеличиваются в раз.

Если же , то аналогично можно получить:

, .

№ 77. Найти современную стоимость месторождения нефти, если ожидается, что доходы от эксплуатации этого месторождения в течение 10 лет составят ежегодно 500 млн. руб., при условии, что реализация продукции производится непрерывно и равномерно, а банковская годовая процентная ставка в течение этих 10 лет ожидается равной 20%.

Решение. Так как то

млн. руб.

Это максимальная сумма, за которую можно продать данное месторождение при начислении 20% процентов в конце каждого года, так как если предположить, что доходы в сумме 500 млн. руб. поступают не непрерывно, а в конце каждого года, то современная стоимость месторождения будет равна

млн. руб.

Если же предположить, что кроме непрерывного поступления платежей, и проценты начисляются непрерывно, то из равенств (гл. 3):

и

можем получить

(40)

и

(41)

где - сила роста.

№ 78. Решить № 77 при условии, что проценты начисляются непрерывно.

Решение. Так как , то

млн. руб.

6.2. Определение срока ренты

Для определения срока непрерывной ренты необходимо решить соответствующие уравнения (по которым вычисляются и ) относительно неизвестной . Например, из уравнения (38):

,

получаем:

то есть

(42)

Аналогично, из уравнения (39), получаем

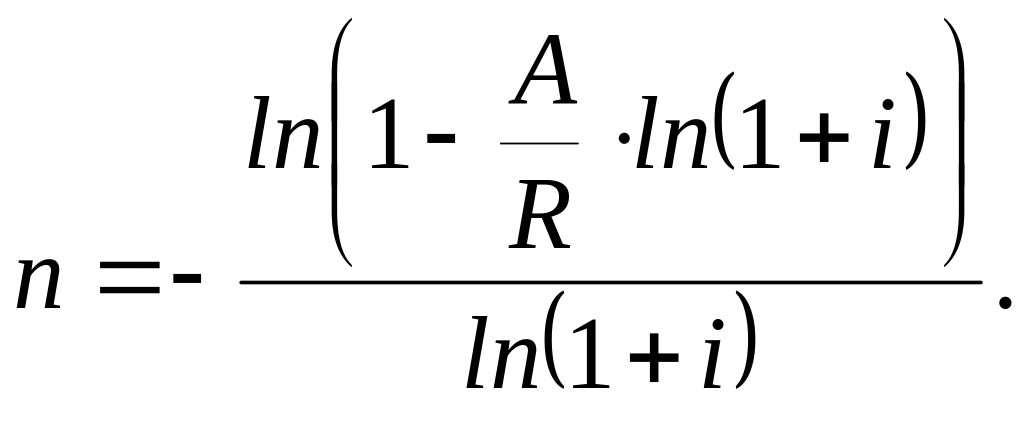(43)

Если же проценты начисляются непрерывно по ставке , то из уравнений (40) и (41) можем получить:

и

№ 79. Месторождение полезных ископаемых было куплено за 2,5 млрд. руб. Ежегодный доход от эксплуатации месторождения прогно-зируется в сумме 500 млн. руб. За какой срок инвестор окупит свои затраты, если на вложенные средства он желает получать ежегодный доход, равный 20%?

Решение. Так как млрд. руб., млн. руб., , то

года 14 лет.

Следует отметить, что если бы ежегодный доход представлял собой разовую выплату в конце года, то срок, за который инвестор окупит свои затраты, был бы равен бесконечности.