3. Определение процентной ставки

Необходимость определения процентной ставки возникает всякий раз, когда речь идет о выяснении эффективности (доходности) финансовой операции. Расчет процентной ставки, в отличие от расчета и , является гораздо более сложной задачей и не имеет аналитического решения. Например, в простейшем случае

и для определения при известных , и требуется решить алгебраическое уравнение n-го порядка:

решение которых возможно лишь при применении компьютеров с соответствующим пакетом прикладных программ численных методов решения уравнений.

Рассмотрим один приближенный способ решения данной задачи, а именно - метод линейной интерполяции (при , ).

По известным (или ) и находим коэффициенты наращения (или приведения) годовой ренты

, или .

Далее, по таблицам Приложений № 4 (или № 5): а) находим: и , или и - соответствующие нижнее и верхнее значения множителей наращения или приведения ренты; б) определяем соответствующие им и – нижнее и верхнее значения предполагаемой процентной ставки.

Тогда для приближенного вычисления процентной ставки можно применить формулы:

(28)

и

. (29)

№ 71. Предприятие решило создать страховой фонд в размере 100 млн. руб., для чего будут производиться ежегодные взносы в банк в размере 16 млн. руб. в течение 5 лет. Определить значение процентной ставки при условии, что взносы и начисление процентов производятся в конце года.

Решение. Так как , и , то коэффициент наращения годовой ренты равен

.

В Приложении № 4 по строке определим два ближайших к 6,25 значения коэффициентов наращения и соответствующих им процентных ставок:

,

и

, .

Следовательно, по формуле (28) получаем:

.

Или .

Вычислим для проверки наращенную сумму

руб.

Таким образом, ставка 11,18% обеспечивает выполнение поставленных условий.

Решить уравнение

относительно неизвестной можно, например, методом Ньютона:

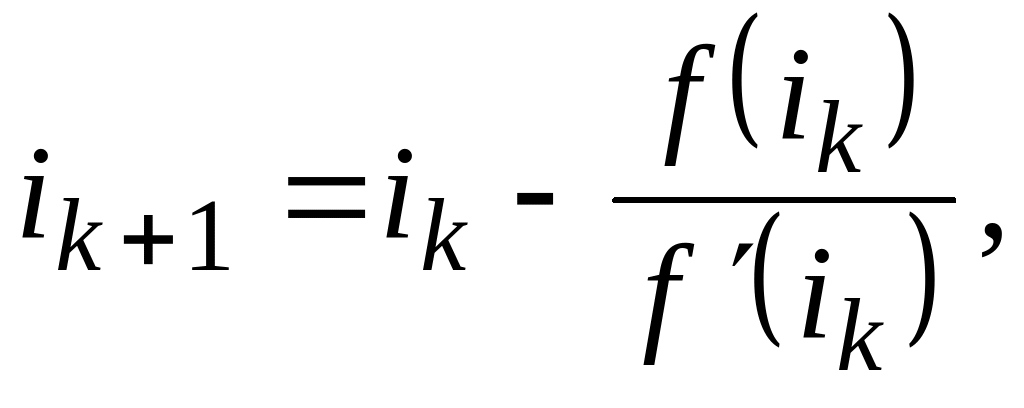
где

А именно,

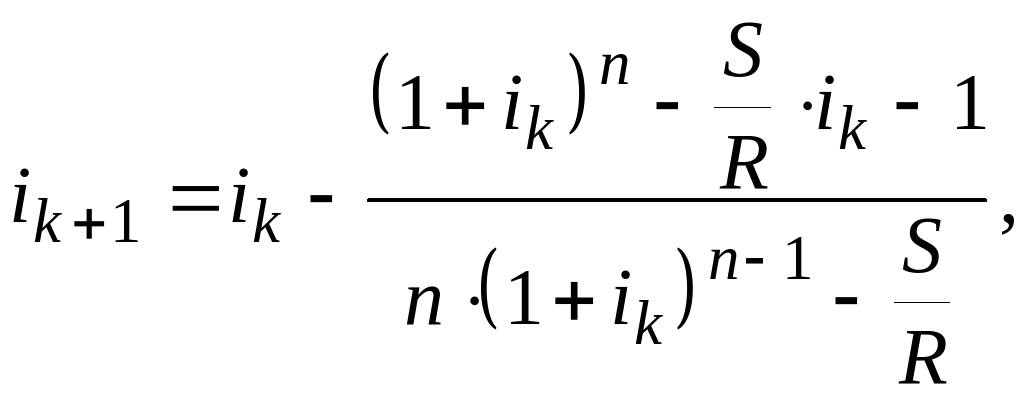
где - номер итерации, а выбирается таким образом, чтобы соответствующий множитель наращения был близок к величине отношения

Аналогичным образом можно найти процентную ставку и при , .

§ 5. Определение параметров других видов постоянных рент

1. Рентные платежи с простыми процентами

Предположим, что рентные платежи производятся один раз в конце года, и начисление простых процентов (i) производится также в конце года. Тогда наращенная за лет сумма представляет собой сумму первых членов арифметической прогрессии:

с первым членом и разностью .

Следовательно,

. (30)

Если рента -срочная, с платежами , производимыми p раз в год, то

. (31)

А расчет современной величины ренты производится по формуле

. (32)

№ 72. Рентные платежи вносятся в течение 3 лет ежеквартально по 50000 руб. Определить наращенную сумму, если проценты начисляются по ставке годовых (простых).

Решение. Так как , , , получаем

тыс. руб.