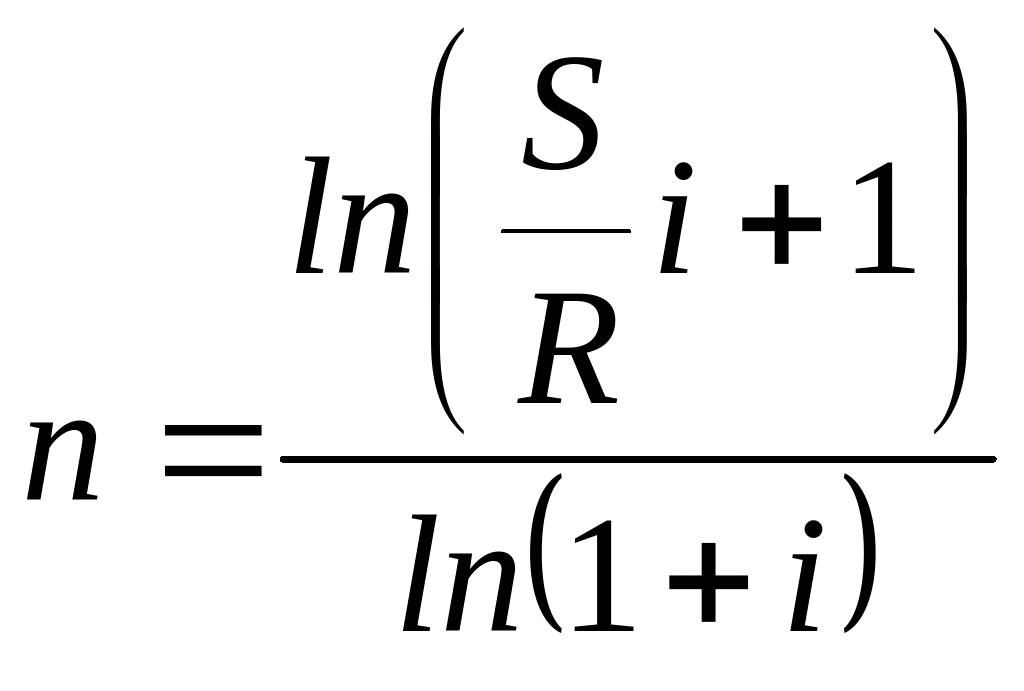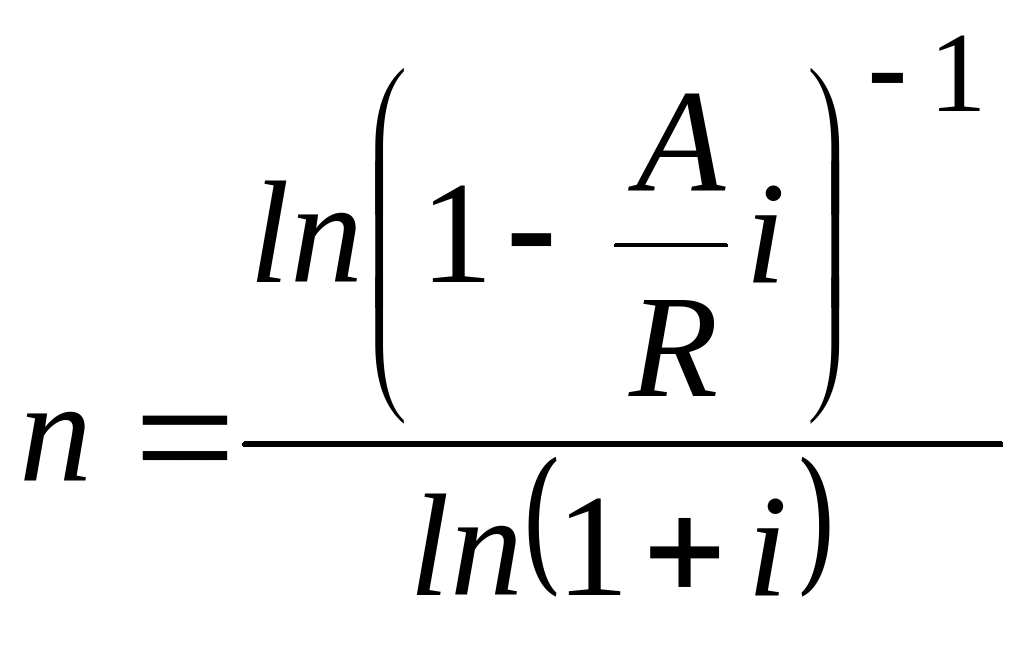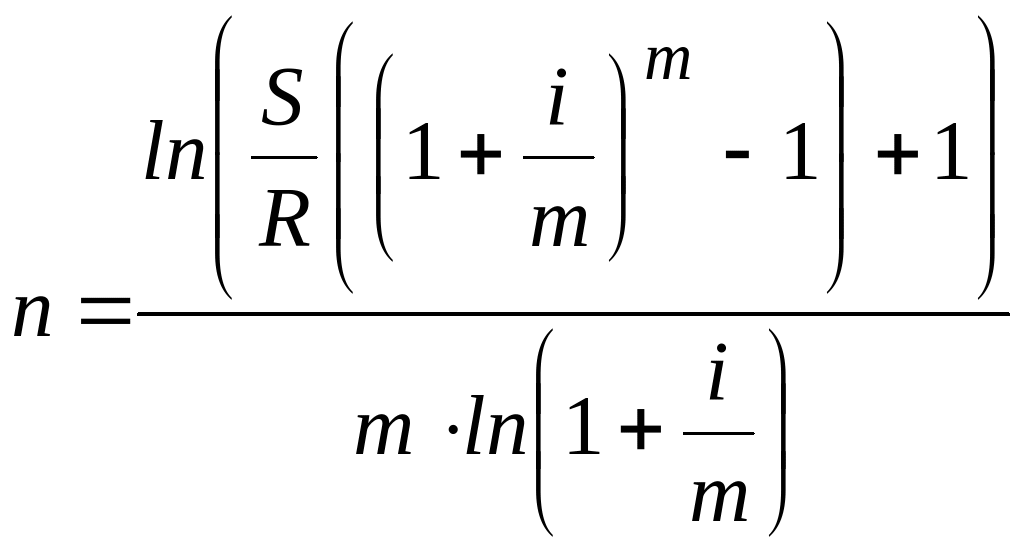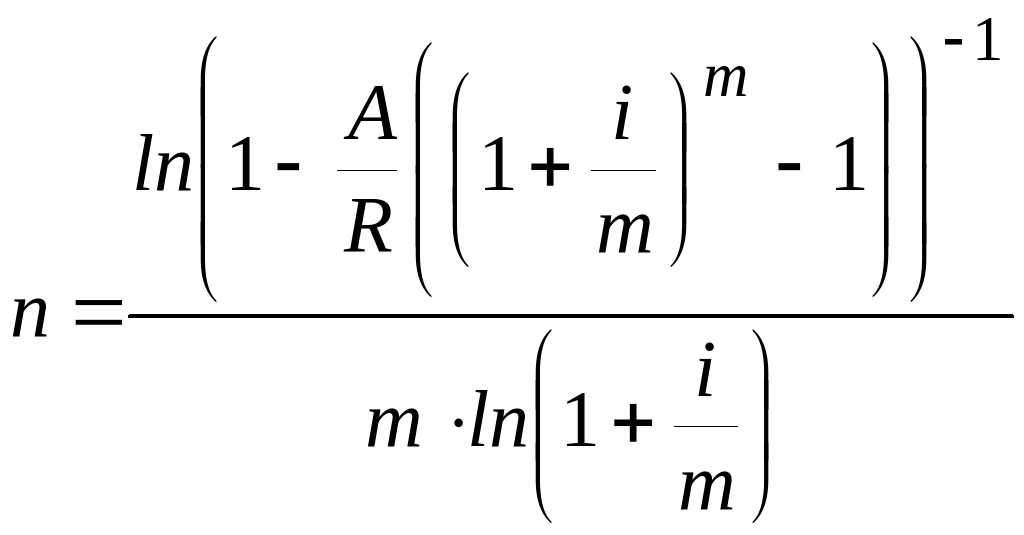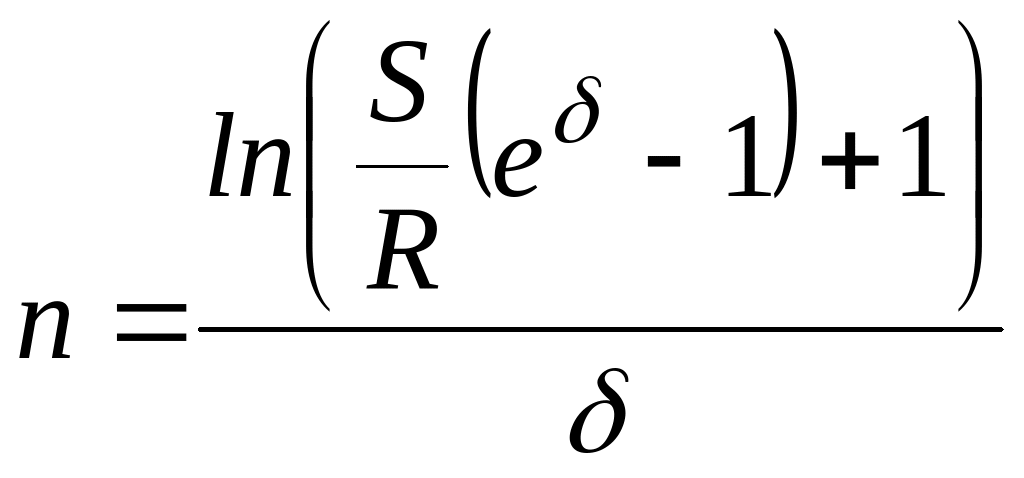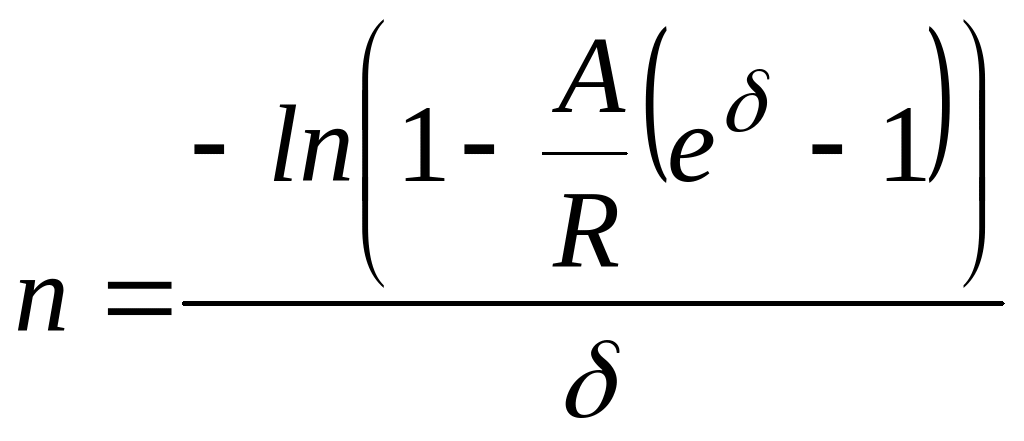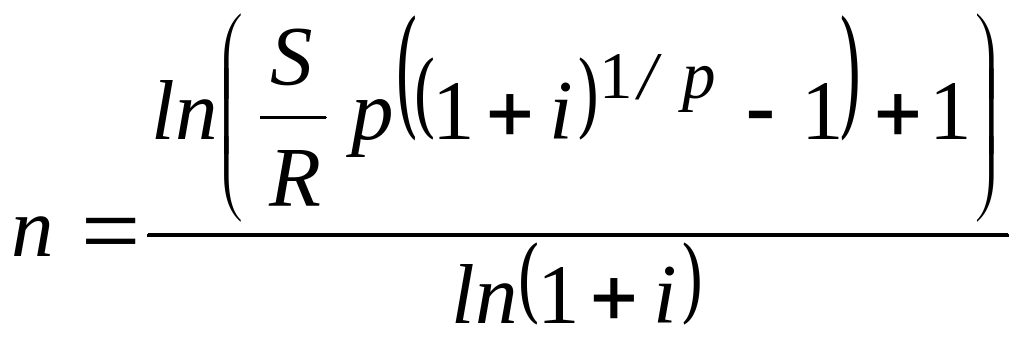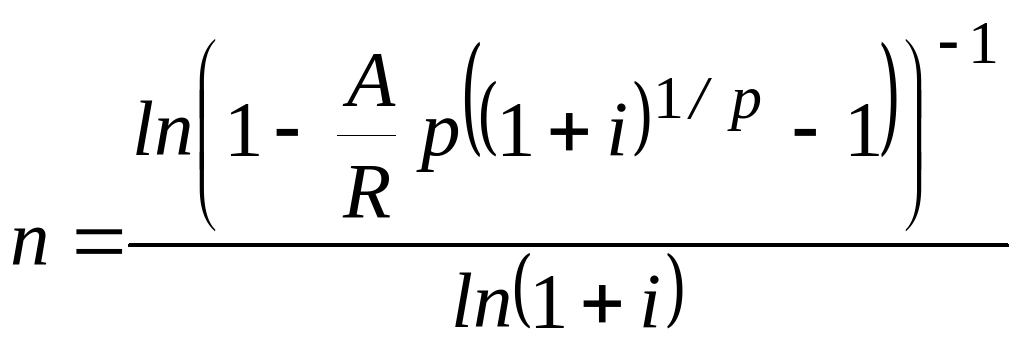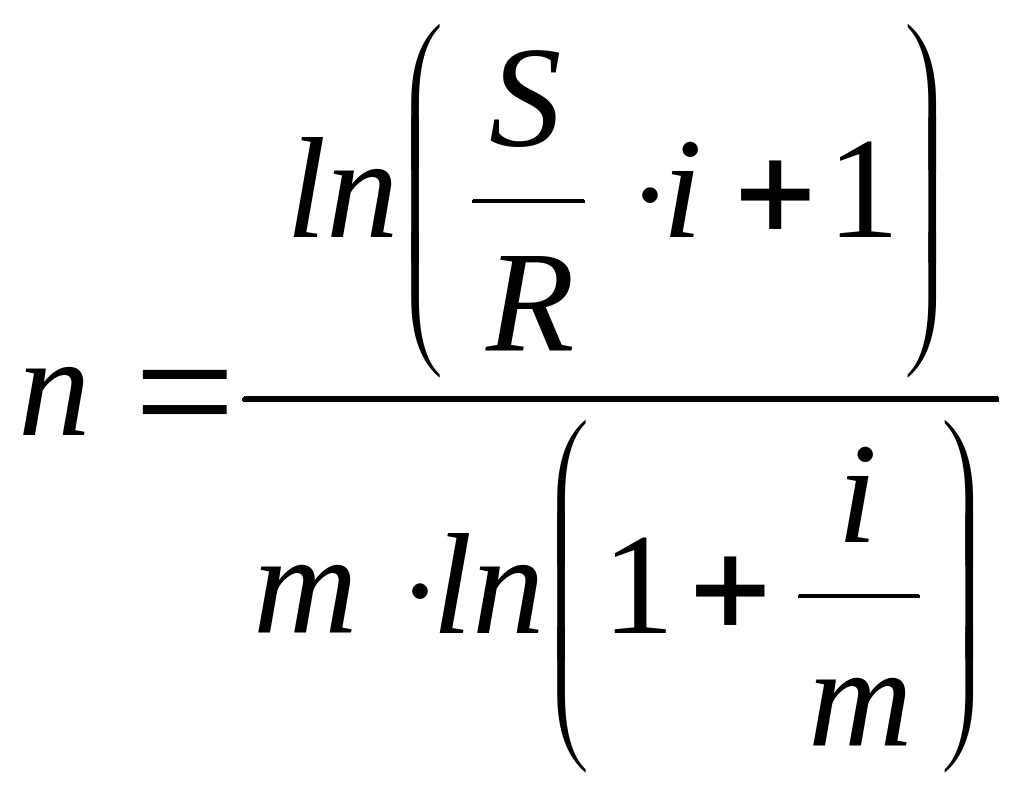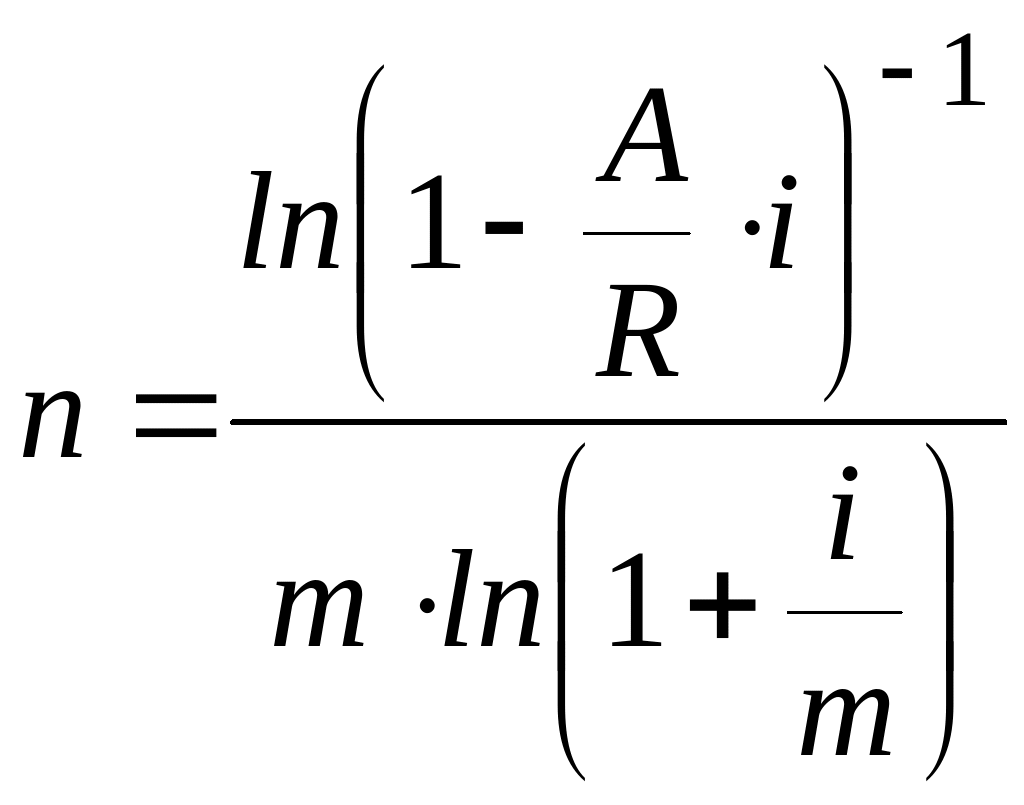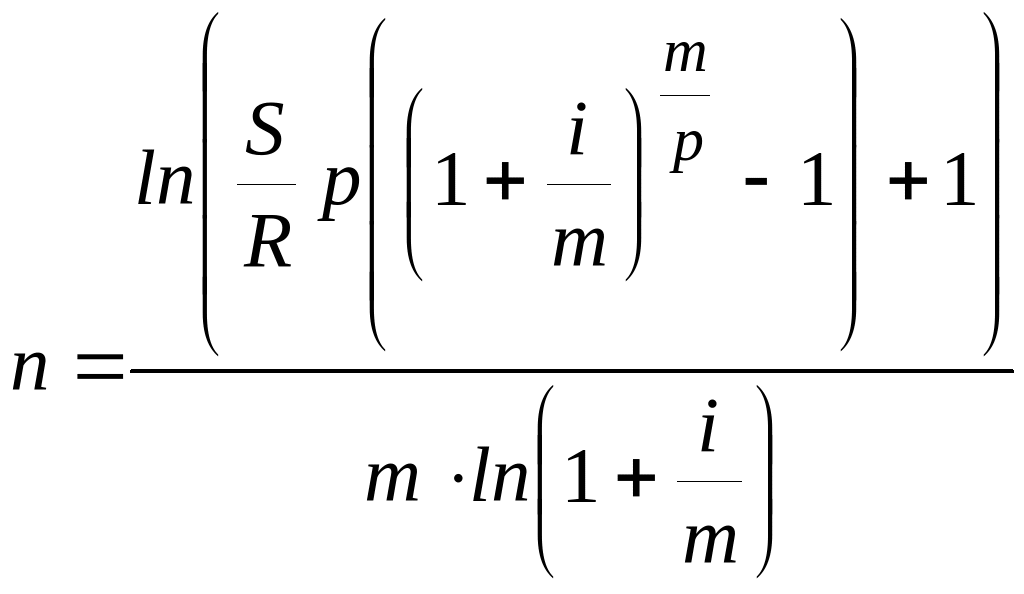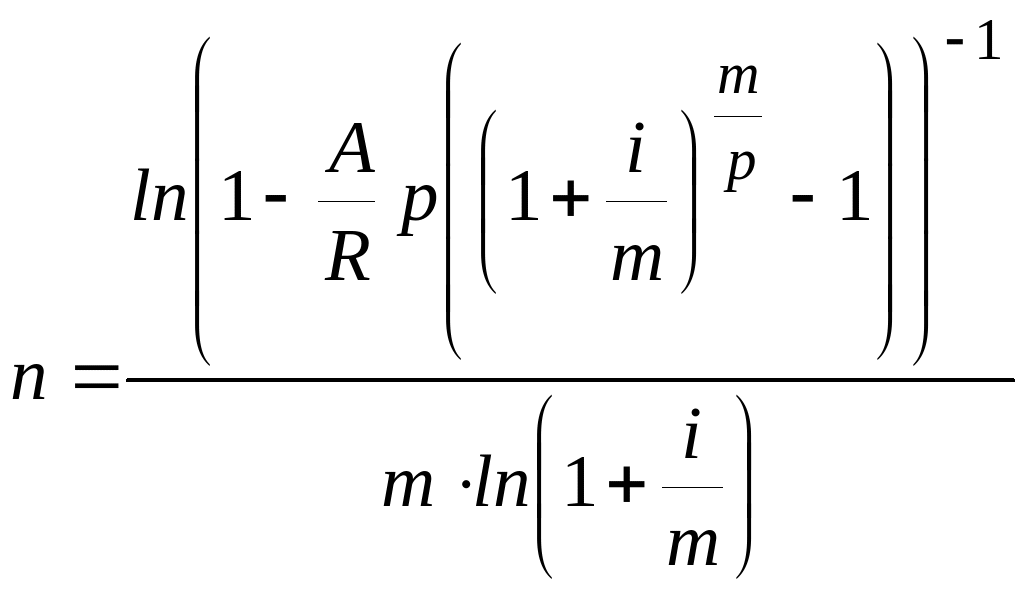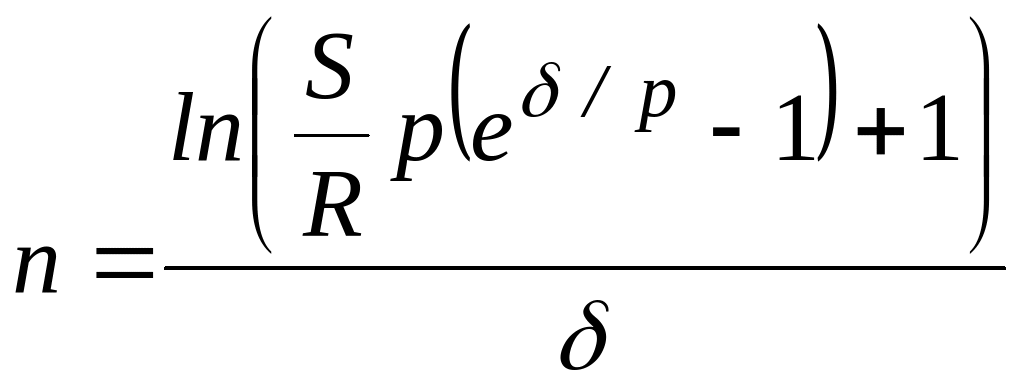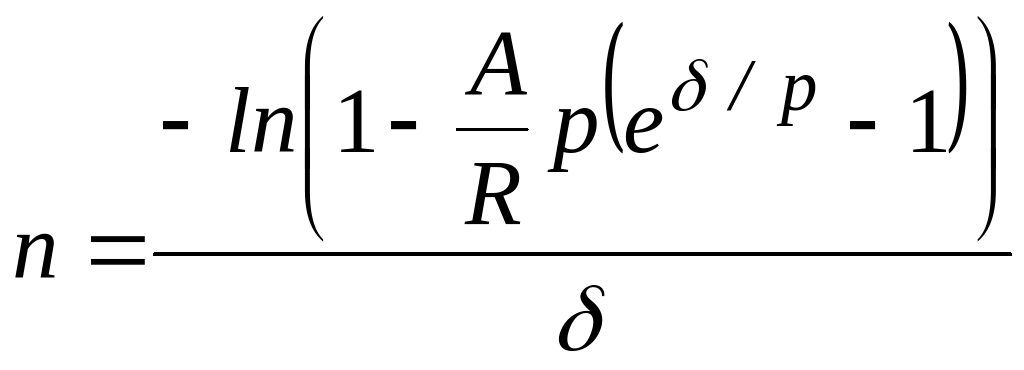- •§ 1. Сущность процентных платежей
- •§ 2. Вычисление наращенных сумм по простой процентной ставке
- •§ 3. Вычисление наращенных сумм на основе простых учетных ставок
- •§ 4. Расчеты в залоговых операциях (ломбардный кредит)
- •§ 5. Потребительский кредит
- •§ 6. Дисконтирование по простым процентам
- •6.1. Сущность дисконтирования
- •6.2. Математическое дисконтирование
- •Банковское дисконтирование (банковский учет)
- •§ 1. Вычисление наращенных сумм на основе сложной процентной ставки
- •1.1. Сущность вычисления платежей по сложной процентной ставке
- •1.2. Проценты за целое число лет
- •1.3. Проценты за дробное число лет
- •Номинальная и эффективная ставка процентов. Наращение процентов m раз в год
- •§ 2 Вычисление наращенных сумм на основе сложных учетных ставок
- •§ 3. Дисконтирование по сложным процентам
- •3.1. Математическое дисконтирование
- •Банковское дисконтирование
- •§4. Сравнение множителей наращения и дисконтирования
- •§ 5 Расчет наращенных сумм с учетом налогов
- •§ 6. Расчет наращенных сумм с учетом инфляции
- •§ 7. Действия с непрерывными процентами
- •§ 1. Финансовая эквивалентность обязательств
- •§ 2. Консолидация платежей
- •2.1. Определение суммы консолидированного платежа
- •2.2. Определение срока консолидированного платежа
- •§ 3. Общий случай изменения условий коммерческих сделок
- •§ 4. Эквивалентность процентных ставок
- •Эквивалентность простых процентных ставок
- •Эквивалентность простых и сложных ставок
- •Эквивалентность сложных ставок
- •Эквивалентность непрерывных и дискретных ставок
- •§ 5. Средние величины в финансовых расчетах
- •5.1. Средние процентные ставки
- •5.2. Средние размеры ссуд
- •§ 6. Пример применения уравнения эквивалентности
- •§ 1. Финансовые ренты. Основные понятия
- •§ 2. Наращенная сумма обычной ренты (постнумерандо)
- •Рента с начислением процентов в конце года
- •2.1.1. Годовая рента
- •Рента с периодом более года
- •. Ренты с начислением процентов раз в год
- •Годовая рента
- •Рента с периодом более одного года
- •Ренты с непрерывным начислением процентов
- •Годовая рента
- •Рента с периодом больше года
- •Сравнение результатов наращения обычной ренты с разными условиями выплат и начисления процентов
- •Погашение долгосрочной задолженности единовременным платежом
- •Инвестиции в предприятия, использующие невосполнимые ресурсы
- •§ 3. Современная величина (ценность) обычной ренты
- •Ренты с начислением процентов в конце года
- •Годовая рента
- •Рента с периодом более года
- •Ренты с начислением процентов m раз в год
- •Годовая рента
- •Рента с периодом больше года
- •Ренты с непрерывным начислением процентов
- •Вечная рента
- •Сравнение современных стоимостей обычной ренты
- •§ 4. Определение параметров постоянных рент (постнумерандо)
- •Определение члена ренты
- •Определение срока ренты
- •Определение процентной ставки
- •§ 5. Определение параметров других видов постоянных рент
- •Рентные платежи с простыми процентами
- •Смешанные ренты
- •Отложенные ренты
- •Рента пренумерандо
- •Ренты с платежами в середине периодов
- •§ 6. Постоянная непрерывная рента
- •6.1. Наращенная сумма и современная стоимость
- •6.2. Определение срока ренты
- •6.3. Определение процентной ставки
- •§ 7. Конверсии постоянных рент
- •7.1. Виды конверсий
- •7.2 Выкуп ренты
- •7.3. Рассрочка платежей
- •7.4. Замена ренты с одними условиями на ренту с другими условиями
- •7.4.1. Замена немедленной ренты на отсроченную
- •7.4.2. Изменение продолжительности и срочности рент
- •7.4.3. Общий случай замены ренты
- •7.5. Консолидация рент
- •§ 1. Ренты с постоянным абсолютным изменением платежей
- •§ 2. Ренты с постоянным относительным изменением платежей
- •§ 3. Переменные непрерывные потоки платежей
- •4.1. Наращенная сумма и современная стоимость
- •4.2. Линейно изменяющийся поток платежей
- •Простые проценты
- •Сложные проценты
- •Эквивалентность финансовых обязательств
- •Финансовые ренты
- •Порядковые номера дней в году
- •Множители наращения (сложные проценты)
- •Множители наращения (сложные проценты)
- •Множители наращения (сложные проценты)
- •Множители наращения (сложные проценты)
- •Множители наращения (сложные проценты)
- •Множители наращения (сложные проценты)
- •Дисконтные множители (сложные проценты),
- •Дисконтные множители (сложные проценты)
- •Дисконтные множители (сложные проценты)
- •Дисконтные множители (сложные проценты)
- •Дисконтные множители (сложные проценты)
- •Дисконтные множители (сложные проценты)
- •Дисконтные множители (сложные проценты)
- •Коэффициенты наращения годовой ренты,
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты наращения годовой ренты
- •Коэффициенты привидения годовой ренты,
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •Коэффициенты привидения годовой ренты
- •424001, Г. Йошкар-Ола, пл. Ленина, 1
§ 4. Определение параметров постоянных рент (постнумерандо)
Как было рассмотрено выше, постоянная
финансовая рента характеризуется
набором основных параметров:
,
,
и допол-нительными параметрами
и
,
при помощи которых вычисляются главные
характеристики ренты: наращенная сумма
и современная стоимость
![]() .
Однако при заключении коммерческих
сделок может возникнуть ситуация, когда
задается одна из главных характеристик
.
Однако при заключении коммерческих
сделок может возникнуть ситуация, когда
задается одна из главных характеристик
![]() или
,
и два основных параметра, и стороны
должны рассчитать величину третьего
основного параметра (или
,
или
,
или
).
или
,
и два основных параметра, и стороны
должны рассчитать величину третьего
основного параметра (или
,
или
,
или
).
Рассмотрим методы расчета недостающего параметра.
Определение члена ренты
Задается или , и срок ренты , процентная ставка . Требуется определить величину разового платежа .
Для решения этой задачи выразим
из соответствующих формул §2
и §3. Например,
если рента выплачивается
раз в год, проценты начисляются один
раз в год по
![]() годовых, и требуется вычислить величину
разового платежа
,
позволяющего получить наращенную сумму
,
то из формулы (3) получаем
годовых, и требуется вычислить величину
разового платежа
,
позволяющего получить наращенную сумму
,
то из формулы (3) получаем
![]() .
.
№ 69. Предприятие решило создать специальный фонд в размере 100 млн. руб., производя ежеквартально платежи в банк под 18% годовых. Требуется определить величину разового платежа, обеспечивающего накопление указанной суммы в течение четырех лет.
Решение. Так как
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() млн. руб.
млн. руб.
То есть предприятие ежеквартально должно вносить в фонд по 4,5 млн. руб.
Определение срока ренты
Пусть задана наращенная сумма (или современная стоимость ), процентная ставка и величина годового платежа . Требуется определить срок ренты .
Для решения этой задачи также используем формулы для вычисления или , выразив из соответствующих равенств неизвестную величину . Так из формулы:
![]() ,
,
получим
![]() ,
,
![]() ,
,
или
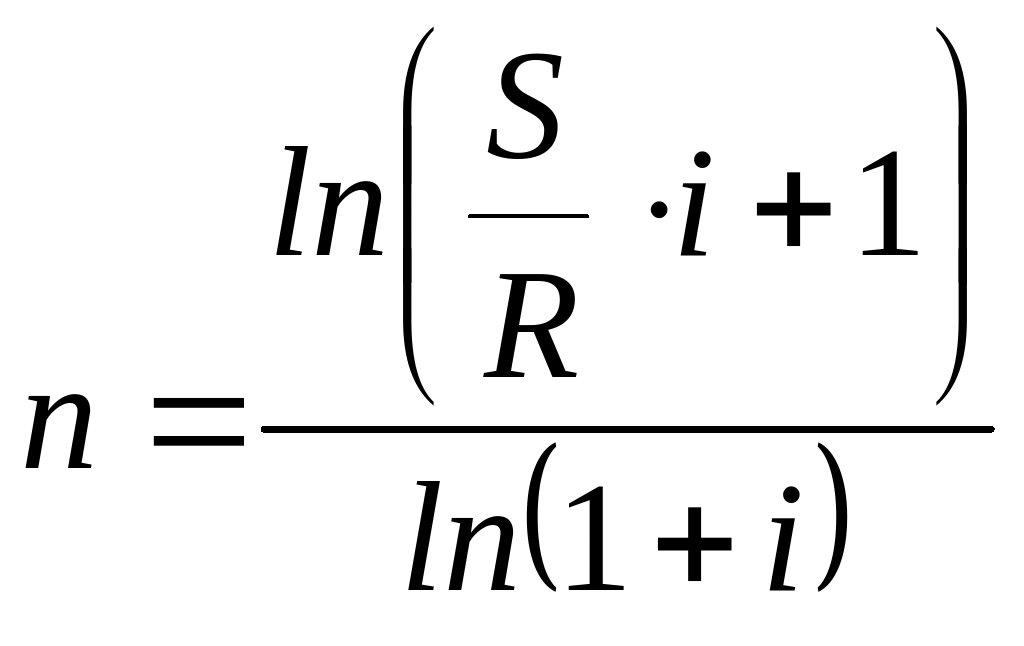 .
.
Аналогичным образом можем получит формулы для расчета сроков и других типов рент, которые приведем в следующей таблице.
Таблица 2
Формулы для расчета продолжительности постоянных рент постнумерандо.
Кол-во рентных |
Кол-во начислений |
Сроки платежей |
|
платежей в году |
процентов в году |
S |
А |
p=1 |
m=1
|
|
|
|
m>1 |
|
|
|
|
|
|
p>1 |
m=1 |
|
|
|
m=p |
|
|
|
|
|
|
|
|
|
|
При расчете сроков ренты следует иметь в виду, что:
Срок ренты, рассчитанный по таблице 1, будет скорее всего величиной дробной, поэтому его необходимо округлить до целого числа лет (обычно до ближайшего меньшего целого числа). Для -срочной ренты – до целого числа округляется величина
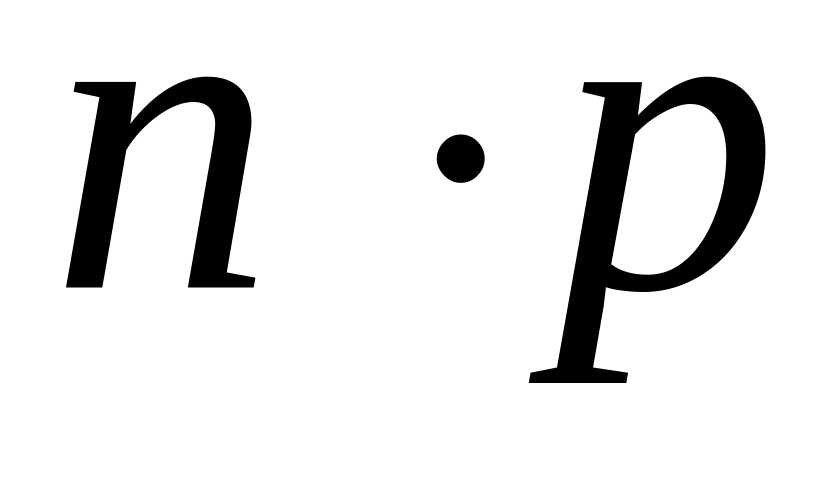 .
Например, если
.
Например, если
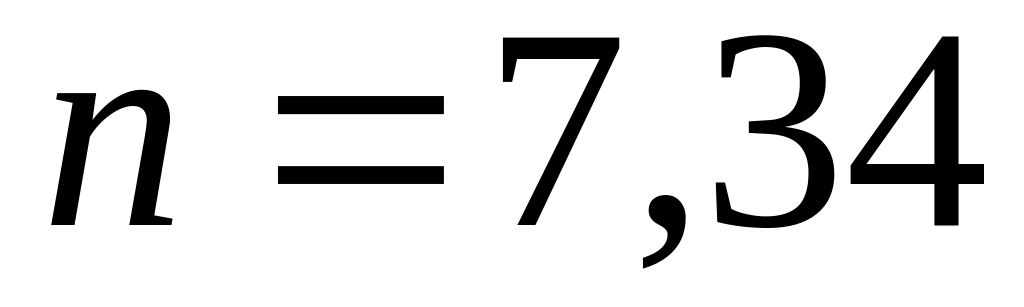 года и
,
то
года и
,
то
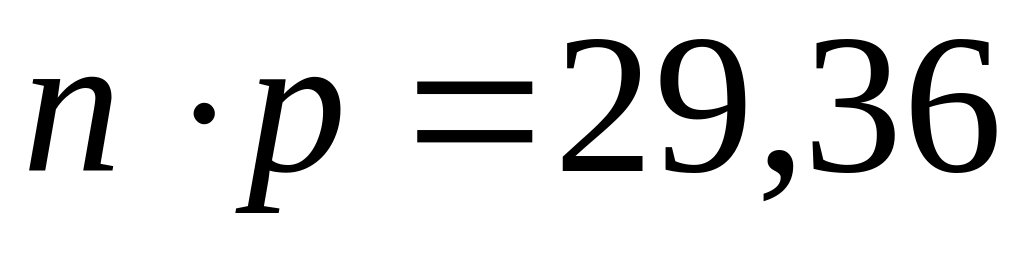 .
Округляем до 29 кварталов.
.
Округляем до 29 кварталов.
В связи с таким округлением уменьшается и наращенная сумма . Поэтому возникает необходимость в соответствующей компенсации, которая может быть осуществлена соответствующим дополнительным платежом или изменением суммы .
Из таблицы видно, что для расчета необходимо выполнение дополнительных условий. Например, из формулы
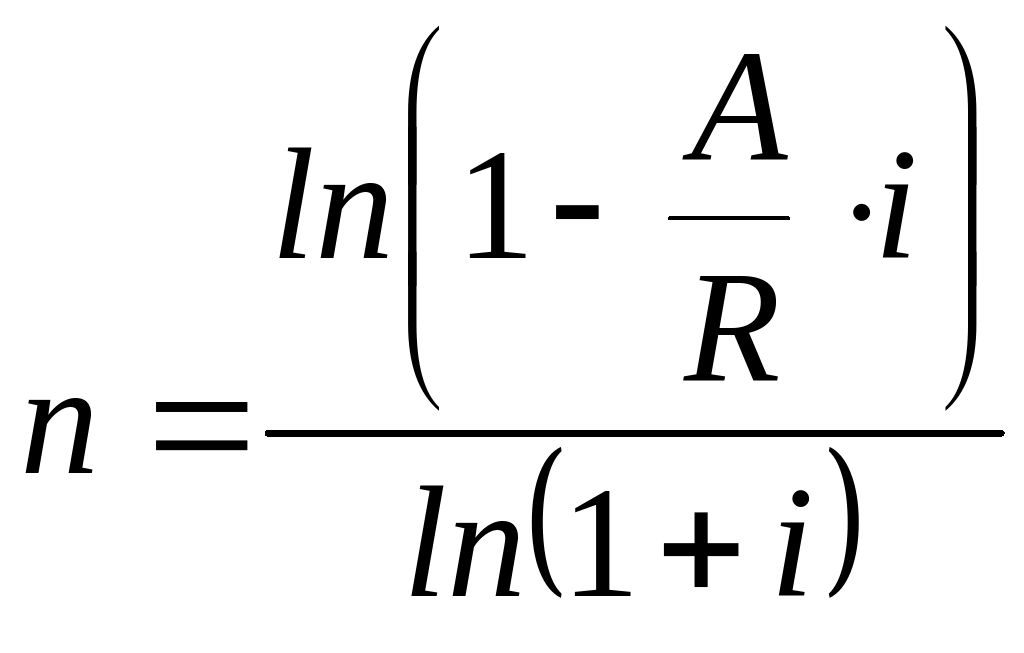
следует, что
![]() или
или
![]() .
Только в этом случае долг может быть
погашен за конечное число лет. Если же
.
Только в этом случае долг может быть
погашен за конечное число лет. Если же
![]() ,
то
,
то
![]() и рента окажется вечной; если
и рента окажется вечной; если
![]() ,
то долг систематически увеличивается.
Аналогичные условия можно получить и
из других формул таблицы 1.
,
то долг систематически увеличивается.
Аналогичные условия можно получить и
из других формул таблицы 1.
№ 70. Клиент берет в банке кредит в размере 15 млн. руб. под 16% годовых. На какой срок банк может выдать кредит, если клиент обязуется производить его погашение равными ежегодными выплатами в конце каждого года по 4 млн. руб.
Решение. Так как
![]() ,
,
![]() ,
,
![]() ,
то
,
то
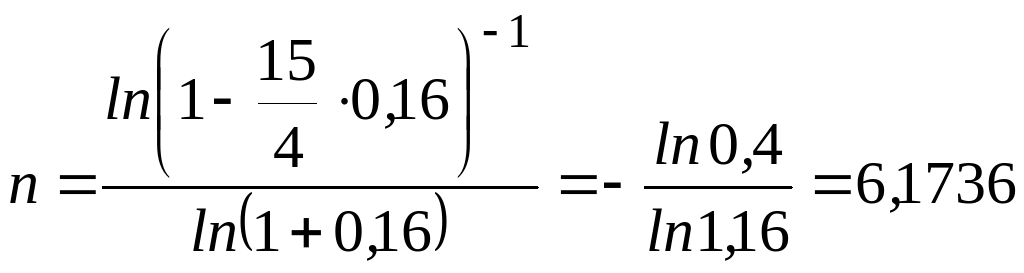 года.
года.
Округляем срок кредита: лет. Тогда современная величина долга составит
![]() руб.,
руб.,
что на 261.056 руб. меньше суммы предполагаемого кредита.
Очевидно, что при банк выдаст кредит в сумме 14.738.944 руб. Если же клиент настаивает на получении кредита в сумме 15 млн. руб., то следует увеличить размер рентного платежа до величины
![]() руб.
руб.