4. Рента с периодом более одного года

В этом случае рента выплачивается каждые раз по руб., а проценты начисляются раз в год. Тогда из формулы (5) получаем:

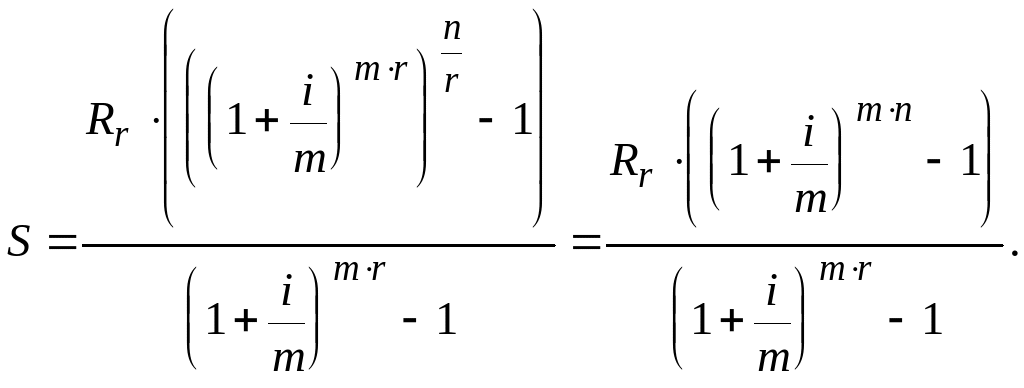(9)

Разделив числитель и знаменатель последней дроби на , получаем:

( )

№ 61. Пусть в условиях № 57 проценты начисляются раз в квартал. Найти наращенную сумму.

Решение. Так как , получаем:

руб.

3. Ренты с непрерывным начислением процентов

1. Годовая рента

В этом случае сумма выплачивается один раз в конце каждого года, и на выплаченную сумму начисляются непрерывные проценты по ставке (силе роста) %. Тогда получим геометрическую прогрессию с первым членом и знаменателем , то есть наращенная за лет сумма равна:

или,

(10)

2. p - срочная рента

В этом случае получаем геометрическую прогрессию с первым членом и знаменателем . И наращенная сумма представляет собой сумму первых членов геометрической прогрессии:

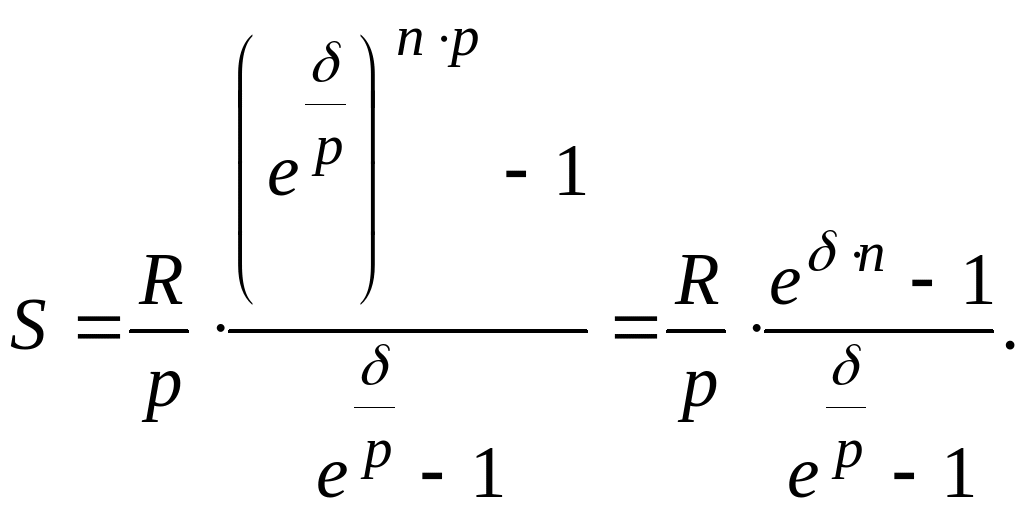(11)

3. Рента с периодом больше года

В этом случае получаем геометрическую прогрессию с первым членом и знаменателем . Тогда наращенная сумма равна сумме первых членов прогрессии:

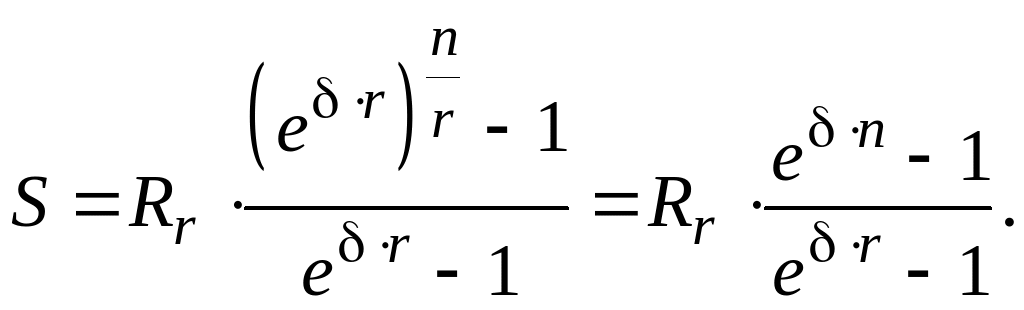(12)

№ 62. Вычислить наращенную сумму в условиях № 55 при условии начисления непрерывных процентов по ставке %, если платежи производятся: а) один раз в год по 1 млн. руб.; б) два раза в год по 500 тыс. руб.; в) раз в два года по 2 млн. руб.

Решение. Так как , то:

а) руб.;

б) руб.;

в) руб.

4. Сравнение результатов наращения обычной ренты с разными условиями выплат и начисления процентов

Из приведенных выше примеров видно, что условия выплат и условия начисления процентов оказывают заметное влияние на величину наращенной суммы. Очевидно, что для практики представляет определенный интерес соотношение этих сумм.

Обозначим сравниваемые наращенные суммы через , где - количество членов ренты в году, - число периодов начислений процентов в год. При непрерывном начислении процентов будем считать Тогда для одних и тех же сумм годовых выплат, продолжительности рент и размеров процентных ставок получим следующие соотношения :

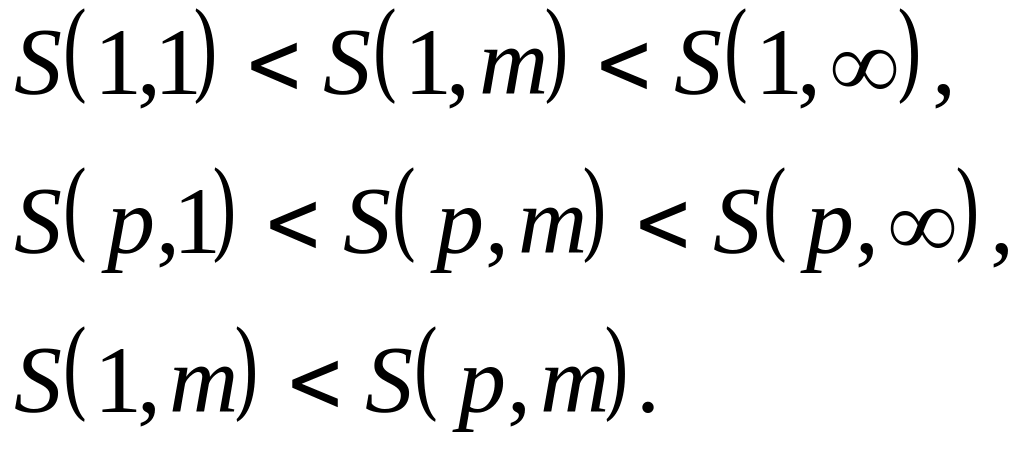
Приведенные неравенства могут быть использованы для получения наиболее выгодных условий при заключении различных финансовых контрактов.

5. Погашение долгосрочной задолженности единовременным платежом

Должник взял ссуду, равную руб., которую должен вернуть через лет. Ежегодно он должен выплачивать кредитору проценты по ставке %. Одновременно он создает погасительный (амортизационный, страховой) фонд, в который делает ежегодные взносы с целью накопить к моменту возвращения долга необходимую сумму. На деньги, находящиеся в фонде, должник получает % в год. Требуется определить так называемую срочную уплату , то есть суммарные ежегодные затраты должника.

Срочная уплата состоит из выплачиваемых на долг процентов, которые равны , и ежегодных взносов в страховой фонд, которые являются членами годовой ренты, состоящей из членов, наращенная сумма которой в момент должна быть равной . Тогда:

(13)

где

№ 63. Ссуда в размере 1 млн. руб. получена под 8% годовых на 4 года. Одновременно с получением ссуды для ее погашения создан страховой фонд, в который делаются равные ежегодные взносы. На деньги, вложенные в фонд, выплачивается 5% годовых. Найти ежегодную срочную уплату по долгу.

Решение:

312.011,83 руб.