Банковское дисконтирование
В этом случае дисконтированная (современная) величина определяется по формуле
(11)
где d - сложная годовая учетная ставка, а дисконт (доход банка) равен
При дисконтировании m раз в году используется номинальная годовая учетная ставка, и расчет производится по формуле
(12)
где f – номинальная
годовая учетная ставка,
– общее число периодов дисконтирования
за n лет.
В этом случае вновь возникает понятие
эффективной ставки
,
которая представляет собой результат
дисконтирования за один год, если
номинальная ставка применяется m
раз в год по
процентов. Для вычисления этой ставки
используем условие равенства
соответствующих дисконтных множителей:
Откуда получаем:
(13)
то есть эффективная учетная ставка меньше номинальной учетной ставки.
№ 26. Долговое обязательство на сумму 6 млн. руб. со сроком погашения через два года было передано в банк для учета по сложной учетной ставке 9%. Определить сумму, полученную владельцем обязательства, если дисконтирование производилось: а) по ежегодной ставке; б) ежеквартально.
Решение. Вычислим сначала для сравнения сумму, которую можно получить при дисконтировании по простой учетной ставке:
млн. руб.
а)
млн. руб.;
б)
млн. руб.
Найдем эффективную учетную ставку:
Видно, что эффективная годовая учетная ставка действительно меньше номинальной, а дисконтирование для клиента наименее выгодно по простой учетной ставке, а наиболее выгодно по сложной учетной ставке, применяемой как можно большее число раз в году.
§4. Сравнение множителей наращения и дисконтирования
Выше, для расчета наращенных
(будущих) и дисконтированных (современных)
сумм использовались различные виды
ставок:
,
,
,
.
Применение в финансовых сделках различных
видов ставок, при прочих равных условиях,
приводит к различным финансовым
результатам, что используется в финансовом
менеджменте для выбора стратегии,
которой должен следовать банк или
коммерческая структура.
Если
,
то соответствующие множители наращения
будут представлять следующий мажорантный
ряд:
а) при 0 < n < 1:
;
б) при n = 1:
;
в) при n > 1:
Для дисконтных множителей получим следующую последовательность неравенств:
а) при 0 < n < 1:
б) при n = 1:
в) при n > 1:
§ 5 Расчет наращенных сумм с учетом налогов
В ряде стран полученные проценты облагаются налогом, что, в конечном итоге, уменьшает реальную наращенную сумму. Кроме того, надо учитывать и то, что частый пересмотр налоговых правил вносит существенный элемент неопределенности в конечные результаты наращения.
Пусть наращенная сумма до выплаты
налогов равна S, а с
учетом выплаты равна
и ставка налога на процентный доход
равна g.
Тогда для простых процентов получаем:
(14)
а величина налога на процентный доход равна:
Таким образом, учет налогов приводит
к уменьшению процентной ставки: вместо
ставки i используется
практически ставка
При начислении налога на сложные проценты в долгосрочных операциях возможны следующие варианты:
Налог начисляется за весь срок сразу:
(15)
Налог начисляется за каждый истекший год. Тогда сумма налога является величиной переменной, так как процентный доход со временем увеличивается. Налог за год
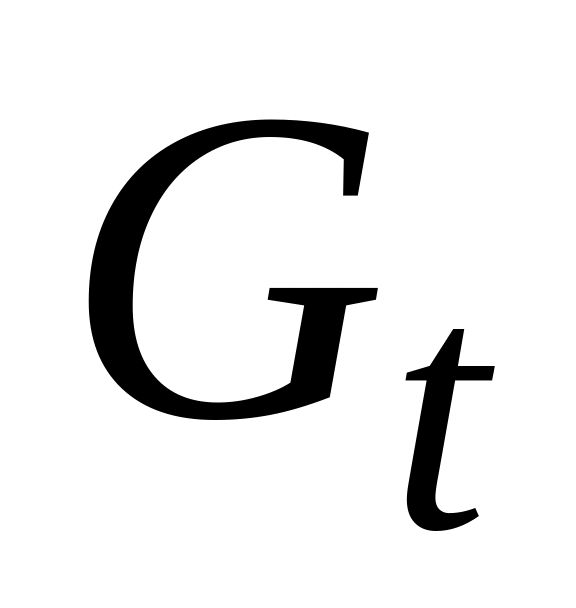(t - номер года)
находится по формуле:
(16)
№ 27. Пусть ставка налога на проценты равна 10%. Процентная ставка – 30%, срок начисления – три года, первоначальная сумма вклада равна 1000 руб. Определить наращенную сумму с учетом выплаты налогов.
Решение. При начислении простых процентов получим наращенную сумму без учета налогов:
руб.;
налог на процентный доход:
наращенную сумму с учетом выплаты налогов:
руб.
При начислении сложных процентов наращенная сумма равна:
руб.;
с учетом налога:
руб.;
сумма налога:
руб.
Если налоги начисляются за каждый год, то:
руб.,
руб.,
руб.
и
