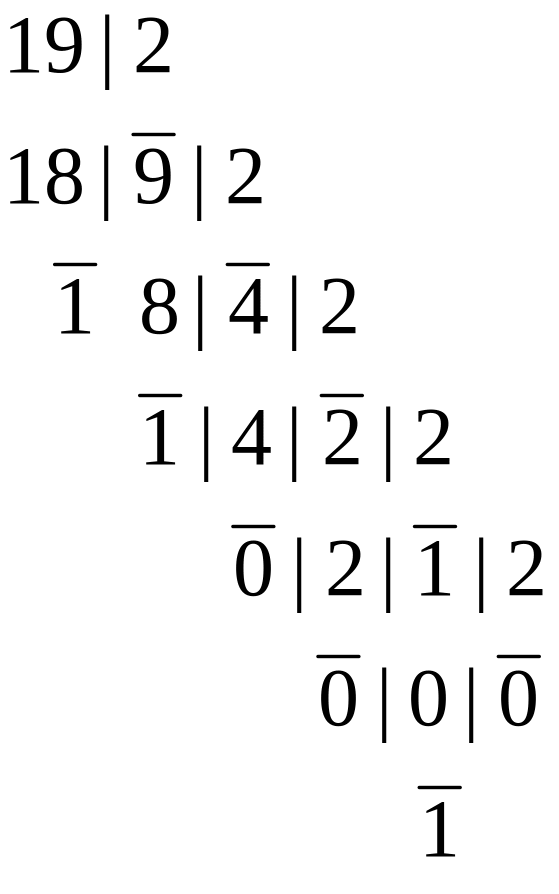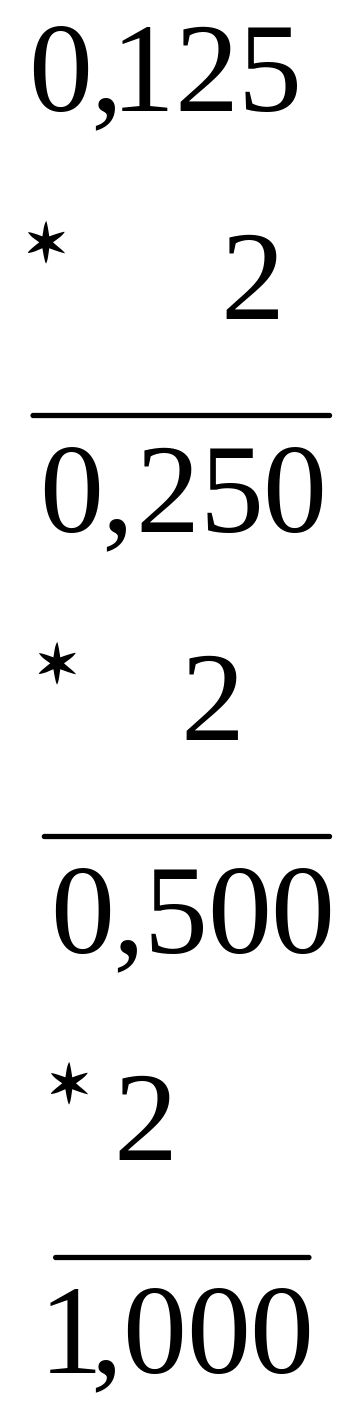- •Утверждено
- •Рецензенты:
- •Содержание
- •Введение
- •1. Цели и задачи дисциплины
- •2. Структура и объем дисциплины
- •3. Содержание дисциплины Распределение фонда времени по темам и видам занятий
- •1.1.2. Выключение компьютера.
- •1.3.13. Закрытие окон.
- •Упражнение 1.4. Настройка операционной системы Windows1.
- •1.4.1. Установка текущей даты и времени.
- •Ознакомьтесь с дополнительными возможностями настройки даты и времени!
- •1.4.2. Изменение заставки на «Рабочем столе».
- •Ознакомьтесь с дополнительными возможностями настройки экрана!
- •1.4.3. Настройка мыши.
- •Ознакомьтесь с дополнительными возможностями настройки мыши!
- •Упражнение 1.5. Форматирование дискеты.
- •2.1.4. Редактирование текстового документа.
- •Упражнение 2.4. Удаление и восстановление папок и файлов.
- •2.4.1. Удаление ярлыка.
- •2.4.2. Удаление сразу нескольких объектов.
- •2.4.3. Восстановление удаленного объекта.
- •3.1.2. Выбор необходимой папки.
- •3.1.3. Создание папки.
- •3.1.4. Открытие папки.
- •3.1.5. Создание файла (текстового документа «Информатика.Txt») в папке.
- •3.1.6. Редактирование текстового документа.
- •3.1.7. Переименование файла.
- •3.1.8. Переименование папки.
- •Упражнение 3.2. Создание ярлыков для папок и файлов.
- •3.2.1. Создание ярлыка для папки.
- •3.2.2. Открытие папки с помощью ярлыка.
- •3.2.3. Создание ярлыка для файла.
- •3.2.4. Открытие файла с помощью ярлыка.
- •3.3.2. Копирование ярлыка из одной папки в другую.
- •3.3.3. Перемещение1 папки из одной папки в другую.
- •Упражнение 3.4. Удаление и восстановление папок и файлов.
- •3.4.1. Удаление ярлыка.
- •3.4.2. Удаление сразу нескольких объектов.
- •3.4.3. Восстановление удаленного объекта.
- •3.4.4. Очищение «Корзины».
- •4.3.2. Вычисление суммы чисел. Вычислим сумму чисел: –5, 10, 30, –25.
- •5.1.4. Закрытие текстового документа.
- •Упражнение 5.2. Открытие и редактирование документа.
- •5.2.1. Открытие текстового документа «Клавиатура.Txt».
- •5.2.2. Редактирование текстового документа. Необходимо добавить новый абзац в конце текста.
- •5.2.3. Сохранение текстового документа под другим именем.
- •5.3.6. Перемещение фрагмента текста.
- •5.4.4. Поиск текста в документе.
- •5.4.5. Замена текста в документе.
- •6.3.2. Закрытие текстового документа.
- •6.3.3. Открытие текстового документа «Системы.Txt».
- •7.1.6. Закрытие рисунка.
- •7.1.7. Открытие документа «Рисунок.Bmp».
- •7.2.7. Рисование прямой линии.
- •7.2.8. Рисование кривой линии.
- •7.2.9. Рисование прямоугольника (или квадрата).
- •7.2.10. Рисование многоугольника.
- •7.2.11. Рисование эллипса (или круга).
- •7.2.12. Рисование скругленного прямоугольника (или квадрата).
- •Упражнение 7.3. Специальные функции программы.
- •7.3.1. Сохранение сжатого рисунка.
- •1.1.2. Настройка внешнего вида окна программы.
- •1.1.3. Настройка параметров архивации.
- •Упражнение 1.2. Создание и преобразование архивов.
- •1.2.1. Выбор объектов для архивирования.
- •1.2.2. Создание обычного1 архива «Обычный.Rar».
- •1.2.3. Создание несжатого архива «Несжатый.Rar».
- •1.2.4. Преобразование несжатого архива.
- •1.2.5. Преобразование архива в самораспаковывающийся5.
- •1.2.6. Создание самораспаковывающегося архива «СамРас.Exe».
- •1.2.7. Преобразование sfx-архива в обычный.
- •Упражнение 1.3. Извлечение и удаление файлов из архивов.
- •1.3.1. Извлечение всех файлов из архива (по умолчанию).
- •1.3.2. Извлечение всех файлов в специальную папку.
- •1.3.3. Извлечение файлов из самораспаковывающегося архива.
- •1.3.4. Удаление файлов из архива.
- •Упражнение 1.4. Специальные функции программы WinRar.
- •1.4.1. Получение информации об архиве.
- •1.4.2. Тест целостности архива.
- •1.4.3. Добавление файлов в существующий архив с помощью мастера.
- •Упражнение 1.5. Работа с архивами в операционной системе Windows (вне утилиты WinRar).
- •1.5.1. Создание архива по умолчанию.
- •1.5.2. Создание архива с выбором параметров архивации.
- •1.5.3. Извлечение всех файлов из архива (по умолчанию).
- •1.5.4. Извлечение файлов из архива в специальную папку.
- •2.1.2. Настройка программы.
- •2.2.3. Проверка выбранных объектов.
- •2.2.4. Приостановка проверки объектов.
- •2.2.5. Проверка всех объектов компьютера.
- •2.2.6. Полная остановка проверки объектов.
- •Упражнение 2.3. Сервисные функции утилиты kav.
- •2.3.1. Просмотр служебной информации о программе.
- •2.3.2. Обновление сигнатур (антивирусных баз).
- •2.3.3. Отмена обновления сигнатур.
- •Упражнение 2.4. Работа с антивирусом в операционной системе Windows (вне утилиты kav).
- •2.4.1. Проверка дискеты.
- •2.4.2. Проверка папки.
- •2.4.3. Проверка нескольких объектов.
- •Упражнение 3.2. Настройка параметров программы.
- •3.2.1. Настройка внешнего вида окна программы.
- •3.2.2. Настройка параметров страницы.
- •3.2.3. Настройка параметров абзаца.
- •3.2.4. Настройка параметров шрифта.
- •3.2.5. Добавление текста в документ. Введем с клавиатуры следующий текст:
- •3.2.6. Сохранение документа «Редактор1.Rtf».
- •Упражнение 3.3. Предварительный просмотр и печать документа.
- •3.3.1. Просмотр документа по две страницы на экране.
- •3.3.2. Печать документа.
- •3.3.3. Закрытие документа.
- •Упражнение 3.4. Редактирование документа.
- •3.4.1. Открытие документа «Редактор1.Rtf».
- •3.4.2. Выделение фрагмента текста с помощью мыши.
- •3.4.8. Выделение строки и абзаца с помощью мыши.
- •Упражнение 3.5. Поиск и замена текста.
- •3.5.1. Поиск одинаковых фрагментов.
- •3.5.2. Поиск одинаковых слов из одной буквы.
- •3.5.3. Поиск прописных букв.
- •3.5.4. Замена слов.
- •3.6.6. Выделение шрифта цветом.
- •3.6.7. Установка выравнивания абзаца. Установим выравнивание второго абзаца1 по правой стороне.
- •3.7.6. Удаление номера в списке. Удалим номер 1 перед первым абзацем2.
- •Упражнение 3.8. Специальное форматирование документа.
- •3.8.1. Создание границ и заливки абзаца текста. Создадим объемную границу синего цвета толщиной 3 и заливку красного цвета с узором 15% в третьем абзаце.
- •3.8.2. Создание колонок текста. Разделим второй абзац на две колонки с расстоянием 1 см между ними.
- •3.9.3. Изменение размера и формы рисунка.
- •3.9.4. Обтекание рисунка текстом.
- •3.9.5. Вставка фигурного текста (объекта WordArt).
- •3.9.6. Вставка формулы. Вставим такую формулу в конец документа:
- •Упражнение 3.11. Работа с таблицей.
- •3.11.1. Добавление таблицы. Создадим таблицу следующего вида:
- •3.13.3. Сохранение шаблона документа.
- •4.1.3. Сохранение документа «Расчет.Xls».
- •Упражнение 4.2. Настройка параметров программы.
- •4.2.1. Настройка внешнего вида окна программы.
- •4.3.5. Закрытие документа.
- •Упражнение 4.4. Редактирование таблицы.
- •4.4.1. Открытие документа «Расчет.Xls».
- •4.4.2. Выделение ячеек.
- •4.4.9. Удаление ячеек.
- •4.4.10. Копирование смежных ячеек с помощью мыши.
- •4.4.11. Создание формул с помощью мыши.
- •4.4.12. Сохранение документа под именем «Расчет1.Xls».
- •Упражнение 4.5. Изменение таблицы.
- •4.5.1. Вставка строки.
- •4.5.2. Вставка столбца.
- •4.6.3. Изменение формул с клавиатуры.
- •4.6.4. Изменение формул с помощью мыши.
- •Упражнение 4.7. Форматирование таблицы.
- •4.7.1. Изменение формата чисел. Установим денежный (р.) формат чисел во всех ячейках с числами.
- •4.7.2. Выравнивание данных в ячейках. Установим выравнивание ячеек с сотрудниками по центру.
- •4.7.3. Изменение шрифта.
- •4.7.4. Обрамление ячеек.
- •4.7.5. Изменение фона ячеек. Установим для группы ячеек с порядковыми номерами желтый фон с узором.
- •4.7.6. Сохранение документа под именем «Расчет2.Xls».
- •Отсортируем таблицу по сотрудникам.
- •4.9.3. Вставка любых функций с помощью мастера функций. Вычислим максимальный размер ндфл.
- •4.9.4. Вставка поля с текущей датой и временем. Вычислим текущую дату и время.
- •4.9.5.Изменение функций.
- •4.10.5. Удаление листа.
- •4.10.6. Копирование ячеек с одного листа на другой.
- •4.11.2. Построение диаграммы для нескольких столбцов (строк) с данными. Построим «гистограмму с накоплением» окладов и премий сотрудников на новом листе.
- •4.11.3. Построение диаграммы долей нескольких столбцов (строк) с данными в общей сумме. Построим «круговую диаграмму» ндфл сотрудников в общей сумме налога на текущем листе.
- •4.11.4. Форматирование диаграммы. Изменим размеры диаграммы.
- •Изменим рамку диаграммы.
- •Изменим фон диаграммы.
- •Изменим рамку, фон и шрифт заголовка диаграммы.
- •4.11.5. Удаление диаграммы с листа.
- •4.11.6. Сохранение документа под именем «Расчет3.Xls».
- •5.1.3. Закрытие базы данных.
- •5.1.4. Открытие базы данных.
- •Упражнение 5.2. Создание таблиц.
- •5.2.1. Создание таблицы в режиме «конструктора».
- •5.2.2. Выбор ключевого поля.
- •Переименуем поля (столбцы).
- •Удалим лишние поля.
- •Заполним таблицу данными, например, следующими:
- •Удалим лишние записи (строки).
- •5.2.6. Сохранение таблицы.
- •5.3.3. Закрытие окна «Схема данных».
- •Упражнение 5.4. Создание форм.
- •5.4.1. Создание формы с помощью «мастера».
- •Закроем форму.
- •5.4.2. Изменение данных таблицы с помощью формы.
- •Упражнение 5.6. Создание запросов.
- •5.6.1. Создание запроса к одной таблице с помощью «мастера».
- •5.6.2. Создание запроса к двум таблицам с помощью «мастера».
- •5.6.4. Создание копии запроса.
- •5.6.5. Открытие запроса в режиме «конструктора». Откроем созданный запрос для изменения в режиме «конструктора».
- •5.6.6. Изменение запроса в режиме «конструктора».
- •5.6.7. Создание итогового запроса с вычислениями. Создадим запрос с помощью «мастера» на подсчет общего количества прихода товаров.
- •Упражнение 5.7. Создание отчетов.
- •5.7.1. Создание отчета к одной таблице с помощью «мастера».
- •5.7.2. Создание отчета к двум таблицам с помощью «мастера».
- •После изучения дисциплины студент должен ответить на следующие вопросы. По теме 1. Понятие информатики и информации:
- •По теме 2. Кодирование информации и ее представление в эвм:
- •По теме 3. Общая характеристика процессов сбора, передачи, обработки и накопления информации:
- •По теме 4. Технические и программные средства реализации информационных процессов:
- •По теме 5. Программное обеспечение эвм и технологии программирования:
- •По теме 6. Алгоритмизация и программирование:
- •По теме 7. Языки программирования высокого уровня, базы данных:
- •По теме 8. Инструментарии функциональных задач:
- •По теме 9. Локальные и глобальные сети эвм:
- •По теме 10. Основы и методы защиты информации:
- •6. Учебно-методическое обеспечение дисциплины
- •6.1. Конспект лекций Введение
- •Понятие информатики и информации.
- •§1.1. Понятие, структура и задачи информатики
- •§1.2. Понятия «информация», «данные», «знания»
- •§1.3. Адекватность и качество информации
- •§1.4. Классификация информации
- •§1.5. Экономическая и правовая информация
- •Кодирование информации и ее представление в эвм.
- •§2.1. Структурные единицы информации
- •§2.2. Кодирование информации
- •§2.3. Системы счисления
- •§2.4. Перевод чисел из одной системы счисления в другую
- •§2.5. Представление информации в эвм
- •Общая характеристика процессов сбора, передачи, обработки и накопления информации.
- •§3.1. Информационная система
- •§3.2. Информационный процесс
- •1. Сбор и регистрация данных.
- •2. Передача информации.
- •3. Ввод информации в компьютер.
- •4. Накопление и хранение информации.
- •5. Обработка информации.
- •§3.3. Информационная технология
- •§3.4. Обеспечение автоматизированных информационных систем
- •1. Информационное обеспечение (ио).
- •2. Техническое обеспечение (то).
- •3. Математическое обеспечение (мо).
- •4. Программное обеспечение (по).
- •5. Лингвистическое обеспечение (ло).
- •6. Организационное обеспечение (оо).
- •7. Правовое обеспечение (ПрО).
- •8. Методическое обеспечение (МтО).
- •9. Эргономическое обеспечение (эо).
- •Технические и программные средства реализации информационных процессов.
- •§4.1. История развития вычислительной техники
- •§4.2. Поколения электронной вычислительной техники
- •§4.3. Классификация вычислительных машин
- •§4.4. Современная классификация компьютеров
- •§4.5. Архитектура и структура эвм
- •§4.6. Общая характеристика персонального компьютера
- •§4.7. Классификация персональных компьютеров
- •Программное обеспечение эвм и технологии программирования.
- •§5.1. Классификация программного обеспечения
- •§5.2. Виды системного программного обеспечения
- •§5.3. Операционные системы
- •§5.4. Виды прикладного программного обеспечения
- •§5.5. Интегрированный пакет Microsoft Office
- •§5.6. Требования к программным продуктам
- •§5.7. Тенденции развития программного обеспечения
- •Алгоритмизация и программирование.
- •§6.1. Понятие и свойства алгоритма
- •§6.2. Способы записи алгоритмов
- •Сначала сформулируем задачу в математическом виде:
- •Словесно-формульная запись алгоритма:
- •§6.3. Типы алгоритмов
- •§6.4. Основные понятия программирования
- •§6.5. Этапы разработки программного обеспечения
- •§6.6. Технологии разработки программного обеспечения
- •§6.7. Структурное программирование
- •§6.8. Объектно-ориентированное программирование
- •Языки программирования высокого уровня, базы данных.
- •§7.1. Системы программирования
- •§ 7.2. Понятия «банк данных», «база данных», «система управления базой данных»
- •§ 7.3. Виды и модели баз данных
- •§ 7.4. Элементы базы данных
- •§ 7.5. Информационно-логическая модель базы данных
- •§ 7.6. Языковые средства баз данных
- •§ 7.7. Субд Microsoft Access
- •Инструментарии функциональных задач.
- •§8.1.1. Виды программ обработки текстовой информации
- •§8.1.2. Стандартные программы обработки текстов
- •§8.2. Текстовый процессор Microsoft Word
- •§8.3. Понятие и возможности табличных процессоров
- •§8.4. Табличный процессор Microsoft Excel
- •§8.5. Общая характеристика справочно-правовых систем
- •§8.6. Справочно-правовые системы «КонсультантПлюс»1
- •Раздел «Законодательство»
- •Раздел «Финансовые консультации»
- •Раздел «Судебная практика»
- •Раздел «Комментарии законодательства»
- •Раздел «Законопроекты»
- •Раздел «Формы документов»
- •Раздел «Международные правовые акты»
- •Раздел «Правовые акты по здравоохранению»
- •Раздел «Технические нормы и правила»
- •Локальные и глобальные сети эвм.
- •§9.1. Вычислительные комплексы и сети
- •§9.2. Функционирование вычислительных сетей
- •§9.3. Локальная вычислительная сеть
- •§9.4. Услуги сети Интернет
- •§9.5. История развития сети Интернет
- •§9.6. Интернет в России
- •Основы и методы защиты информации.
- •§10.1. Необходимость защиты информации
- •§10.2. Методы защиты информации
- •§10.3. Компьютерные вирусы
- •§10.4. Классификация компьютерных вирусов
- •§10.5. Антивирусные программы
- •§10.6. Архивация данных
- •6.2. Методические указания студентам
- •6.2.1. Общие рекомендации
- •6.2.2. Методические указания и задания на выполнение контрольной работы (очно-заочное и заочное отделение)
- •6.3. Литература
- •7. Требования к уровню освоения программы и формы текущего, промежуточного и итогового контроля
- •7.1. Формы текущего, промежуточного и итогового контроля
- •7.2. Тесты самопроверки знаний
- •7.2.1. По теме 1. Понятие информатики и информации:
- •7.2.2. По теме 2. Кодирование информации и ее представление в эвм:
- •7.2.3. По теме 3. Общая характеристика процессов сбора, передачи, обработки и накопления информации:
- •7.2.4. По теме 4. Технические и программные средства реализации информационных процессов:
- •7.2.5. По теме 5. Программное обеспечение эвм и технологии программирования:
- •7.2.6. По теме 6. Алгоритмизация и программирование:
- •7.2.7. По теме 7. Языки программирования высокого уровня, базы данных:
- •7.2.8. По теме 8. Инструментарии функциональных задач:
- •7.2.9. По теме 9. Локальные и глобальные сети эвм:
- •7.2.10. По теме 10. Основы и методы защиты информации:
- •7.3. Правильные ответы на тесты самопроверки знаний Ответы по тестам темы 1:
- •Ответы по тестам темы 6:
- •Ответы по тестам темы 7:
- •Ответы по тестам темы 8:
- •Ответы по тестам темы 9:
- •Ответы по тестам темы 10:
- •Вопросы к зачету (2 семестр)
- •Вопросы к экзамену (3 семестр)
- •11. Тематика курсовых, дипломных работ и рефератов
§2.3. Системы счисления
В повседневной жизни мы имеем дело с десятичной системой счисления, в основном, используя арабские цифры. В то же время в электронных вычислительных машинах (ЭВМ) информация кодируется в двоичной системе счисления.
Система счисления – это способ наименования и изображения чисел с помощью символов (цифр), имеющих определенные количественные значения.
В зависимости от способа изображения чисел выделяется два типа систем счисления:
позиционные системы счисления, в которых количественное значение каждой цифры зависит от ее места (позиции) в числе, например, арабская система счисления;
непозиционные системы счисления, в которых цифры не меняют своего количественного значения при смене позиции в числе, например, римская система счисления.
Основание позиционной системы счисления (P) – это количество различных цифр, используемых для изображения чисел в системе счисления. При этом сами значения цифр лежат в пределах от 0 до P-1.
В позиционной системе счисления любое число представляется суммой произведений коэффициентов (цифр, из которых состоит число) на основание системы счисления в степени, соответствующей местоположению цифры в числе. При этом первой цифре целой части числа (слева от запятой) соответствует позиция 0, второй 1 и т.д., а первой цифре дробной части числа (справа от запятой) соответствует позиция -1, второй -2 и т.д.
В общем случае любое число A, состоящее из m знаков в целой части и n знаков в дробной части, в позиционной системе счисления с основанием P будет записано в следующем виде:
A=am-1*Pm-1+…+a1*P1+a0*P0+a-1P-1+…a-n*P-n (1)
где нижние индексы 0…m-1 определяют местоположение цифры в целой части числа, а индексы -1…-n – соответственно, в дробной.
Максимальное число, которое может быть представлено в m разрядах целой части числа, выражается формулой: Amax=Pm–1
Минимальное значащее (не равное 0) число, которое можно записать в n разрядах дробной части, выражается формулой: Amin=P-n
Основные данные по системам счисления (основание и используемые символы) представлены в табл. 2.1.
Таблица 2.1
Характеристика систем счисления
Система счисления |
Основание |
Используемые символы (коэффициенты) |
Десятичная |
10 |
0 – 9 |
Двоичная |
2 |
0 – 1 |
Восьмеричная |
8 |
0 – 7 |
Шестнадцатеричная |
16 |
0 – 9, A(10), B(11), C(12), D(13), E(14), F(15) |
Десятичное число
357,4(10)=3*102+5*101+7*100+4*10-1
Двоичное число
10110,1(2)=1*24+0*23+1*22+1*21+0*20+1*2-1=16+4+2+0,5=22,5(10)
Восьмеричное число
357,4(8)=3*82+5*81+7*80+4*8-1=192+40+7+0,5=239,5(10)
Шестнадцатеричное число
3BE,4(16)=3*162+11*161+14*160+4*16-1=768+176+14+0,25=958,25(10)
§2.4. Перевод чисел из одной системы счисления в другую
Для перевода числа из десятичной системы счисления в двоичную (восьмеричную или шестнадцатеричную):
для целой части числа используется метод последовательного деления на основание новой системы счисления, то есть на 2 (8 или 16). Деление продолжается до тех пор, пока результат деления не будет равен 0. В этом случае остаток всегда будет меньше основания новой системы счисления, то есть 1 (для двоичной системы счисления), от 1 до 7 (для восьмеричной системы счисления) или от 1 до 15 (для шестнадцатеричной системы счисления). Для составления нового числа необходимо записать полученные остатки от деления в обратном порядке;
для дробной части числа используется метод последовательного умножения на основание новой системы счисления, то есть на 2 (8 или 16). Целая часть результата умножения используется для записи числа, а дробная снова умножается на основание новой системы счисления. Умножение продолжается до тех пор, пока дробная часть не станет равной 0 или не будет достигнута требуемая точность перевода.
Например, переведем десятичное число 19,125(10) в двоичную систему счисления.
Целую часть (19) последовательно делим на 2:
|
Дробную часть (0,125) умножаем на 2:
|
Итак, новое число запишется следующим образом:
19,125(10)=10011,001(2)
Аналогично переводятся десятичные числа в восьмеричные и шестнадцатеричные.
Для обратного перевода двоичных (восьмеричных и шестнадцатеричных) чисел в десятичные необходимо представить их по формуле (1) и рассчитать соответствующую сумму.
Для перевода числа из двоичной системы счисления в восьмеричную или шестнадцатеричную необходимо разбить исходное двоичное число на триады1 (для восьмеричной СС) или тетрады2 (для шестнадцатеричной СС), а затем заменить каждую триаду или тетраду соответствующей восьмеричной или шестнадцатеричной цифрой. Для целой части числа триады (тетрады) формируются от запятой справа налево, для дробной – слева направо. Недостающие двоичные цифры заменяются 0.
Например, двоичное число 11101111,1(2) в восьмеричной системе счисления будет представлено так:
011 101 111,100(2)=357,4(8)
То же самое двоичное число 11101111,1(2) в шестнадцатеричной системе счисления будет представлено так:
1110 1111,1000(2)=EF,8(16)
Для обратного перевода восьмеричных или шестнадцатеричных чисел в двоичные необходимо каждую восьмеричную или шестнадцатеричную цифру заменить соответствующей триадой или тетрадой из двоичных цифр.
Например, восьмеричное число 315(8) в двоичной системе счисления будет представлено так:
315,6(8)=011 001 101,110(2)=11001101,11(2)
Шестнадцатеричное число 3BE,4 (16) в двоичной системе счисления будет представлено так:
3BE,4(16)=0011 1011 1110,0100(2)=1110111110,01(2)