55. Сбалансированный рост в однопродуктовой макродинамической модели с запаздыванием

Главное допущение рассмотренной в параграфе 4.1 модели состояло в том, что инвестиции превращаются в фонды мгновенно. Как уже отмечалось, такое предположение не может быть принято безоговорочно, т.к. освоение капиталовложений всегда происходит с определенным лагом (запаздыванием). В связи с этим возникает вопрос: как влияет лаг на основные показатели экономического роста?

В дальнейшем будем считать, что процесс ввода инвестиций в действие является непрерывным и стационарным с экспоненциальным законом запаздывания (26.5). Тогда движение фондов будет описано дифференциальными уравнениями (26.2, 26.7). Соотношение (4.3, 4.4) лекций, не зависящие от процесса создания фондов, разумеется, останутся в силе. Выпишем все уравнения модели:

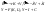(1)

Это модель, как и предыдущая, не замкнута. Для ее замыкания надо задать функцию или . Предположим, как и прежде, что рост трудовых ресурсов происходит с постоянным темпом , т.е. . Тогда данную модель можно рассматривать как систему управления, в которой роль управляющего воздействия играет или .

Введем в рассмотрение относительные переменные - фонды, входящие в строй на единицу рабочей силы.

Из (1) следует (2)

В этом можно убедиться с помощью преобразований, аналогичных тем, которые применялись в пар 4.3 лекционного конспекта.

Напомним, что под сбалансированным ростом понимается такой процесс развития экономики, при котором основные макропеременные изменяются с постоянным темпом. С помощью рассуждений, почти ничем не отличающихся от тех, которые использовались в параграфе 4.4 лекционного конспекта можно показать, что темпы роста всех показателей совпадают и равны (Это относится и к ). Отсюда следует, что при сбалансированном росте величины постоянны (не зависят от времени). Таким образом, сбалансированному росту соответствует постоянные решения (положение равновесия, точка покоя) 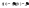системы дифференциальных уравнений (2), в которой . Найдя такое решение, можно легко определить основные макропеременные (см формулы 4.19 лекционного конспекта).

Покажем, что, как и в модели без запаздывания, для каждой фиксированной постоянной нормы накопления существует единственная траектория сбалансированного роста. Для этого достаточно убедиться, что система конечных уравнений

(3)

имеет в области единственное решение.

Выразим из первого уравнения (3) и полученное выражение подставим во второе. В результате будем иметь (4)

Функция 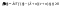имеет тот же вид, что и функция , определенная формулой 4.21 лекционного конспекта. Поэтому, повторяя почти дословно приведенное в пар 4.4 лекционного конспекта рассуждение, убеждаемся в том, что уравнение (4) имеет в области единственное решение (РИСУНОК)

Тогда будет решение системы (3), причем других решений в нашей области нет. Заметим, что в случае функции Кобба-Дугласа 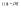, и, соответственно, .

Итак, в рассмотренной модели для каждой фиксированной постоянной нормы накопления существует единственная траектория сбалансированного роста. Заметим, что, как и в модели без запаздывания, при увеличении нормы накопления возрастает и фондовооруженность на траектории сбалансированного роста.

В параграфе 4.5 лекционного конспекта было показано, что в модели Солоу без запаздывания любая траектория с постоянной нормой накопления с течением времени неограниченно приближается к траектории сбалансированного роста. Выясним, сохраняется ли это свойство в рассматриваемом случае.

Пусть

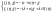
В силу теоремы об устойчивости по первому приближению положение равновесия системы (2) будет асимптотически устойчивым, если характеристические числа матрицы Якоби имеют отрицательные действительные части.

=

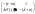
Эти числа – корни характеристического уравнения , где

Согласно критерию Гурвица, Для отрицательности действ частей корней такого уравнения необходимо и достаточно . Первое неравенство, очевидно, имеет место. Второе также справедливо, поскольку 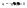(см рисунок с функцией ). Таким образом, постоянное решение системы (2), соответствующее сбалансированному росту, асимптотически устойчиво.

Заметим, что в данном случае, в отличие от модели без запаздывания, мы не можем говорить о сходимости к траектории сбалансированного роста всех траекторий с постоянной нормой накопления. Во всяком случае, это не следует из приведенных рассуждений.