50. Независимость производственного процесса от масштаба

Предположим, что имеется одинаковых заводов, выпускающих один и тот же продукт. Допустим далее, что построили еще один такой завод и наняли на него требуемую рабочую силу. В результате и объем фондов по выпуску данного продукта, и численность занятых увеличились в 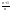раз. Понятно, что и выпуск продукта увеличится во столько же раз. Перейдем к макропеременным.

Приведенный пример наводит на мысль о справедливости следующего утверждения: если и фонды, и рабочую силу изменить в одно и то же число раз, то при прежней технологи выпуск изменится во столько же раз. Это свойство производственного процесса называется независимостью от масштаба. Смысл такого названия станет понятен, если учесть, что изменение в раз факторов производства можно рассматривать просто как изменение масштаба, единицы измерения.

Сформулированное свойство иногда вызывает возражением. Вот типичный контраргумент: если вам нужны две-три уникальные детали, то их можно сделать вручную. Но если понадобятся тысячи, то проще и дешевле, построив специальный завод, выпускать их на конвейере. При этом выпуск увеличится в большее число раз, чем затраты на факторы производства. Этот пример, однако, не совсем корректен, ибо построение завода в данном случае означает изменение технологии и, в конечном счете, производственной функции. Статистика, как правило, подтверждает справедливость правила о независимости от масштаба. Мы будем считать в дальнейшем, что это предположение выполнено.

Математически независимость от масштаба формулируется следующим образом:

(5)

Это означает, что производственная функция является однородной первой степени (линейно однородной). Заметим, что функция Кобба-Дугласа и функция с постоянной эластичностью замены (см §1.9) этим свойством обладают.

Свойство независимости от масштаба позволяет вместо переменных использовать их отношение 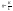. Величина равна количеству фондов, приходящихся на единицу рабочей силы, и называется фондовооруженностью или капиталовооруженностью.

Полагая в (5) 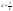, получаем 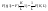(6)

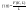Обозначим . В силу (6): (7)

Величина в правой части этого равенства есть выпуск продукта на единицу рабочей силы, т.е. средняя производительность труда. Обозначим ее через и запишем равенство (7) в виде (8)

Таким образом, функция характеризует зависимость производительность труда от фондовооруженности. Из свойств производственной функции (см §1.9) следует, что - возрастающая вогнутая функция. В дальнейшем будем считать, что она дважды непрерывно дифференцируема в области и в каждой точке

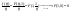Для производственной функции, описывающей экономическую систему в целом, естественным выглядит предположение , которое является отражением того, что без фондов или рабочей силы выпуск продукта невозможен. Тогда и (9)

Отсюда в частности видно, что при достаточно больших функция растет медленнее, чем линейная. Обычно считают, что 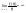(10),

то есть при достаточно малых функция растет быстрее, чем линейная. Это предположение является отражением того, что увеличение фондовооруженности при достаточно малых ее значениях приводит к значительному росту производительности труда. В дальнейшем будем считать, что условие (10) выполнено.