53. Асимптотическое поведение траектории в модели Солоу

Режим сбалансированного роста – это, вообще говоря, одна из возможных траекторий развития экономических систем. Если данная модель используется для описания реальной экономики, то любая конкретная траектория будет определяться как решение дифференциального уравнения (16) с начальным условием - значением фондовооруженности в начальный момент времени и необязательно является траекторией сбалансированного роста (как правило не является). Вместе с тем, как будет показано в дальнейшем, траектории сбалансированного роста играют важную роль среди множества траекторий рассматриваемой модели, а именно: любая траектория с постоянной нормой накопления по прошествии достаточно большого времени неограничено приближается к траектории сбалансированного роста. Следовательно, режим сбалансированного роста может быть использован для расчетов экономических показателей при достаточно больших значениях времени, независимо от начальных значений этих показателей.

С математической точки зрения описанное свойство траектории модели выглядит следующим образом:

Пусть - фиксированное постоянное значение нормы накопления. - фондовооруженность на соответствующей этой норме траектории сбалансированного роста. - решение дифференциального уравнения (16) с начальным условием . Тогда независимо от значения , справедливо соотношение

(22)

Докажем это. Предположим сначала, что . В предыдущем параграфе мы выяснили, что правая часть уравнения (16) (функция (21)) принимает в области положительные значения. Поэтому функция будет монотонно возрастать, пока ее значения принадлежат этой области. Легко видеть, что не покинет область ни при каком . Действительно, допустив противное, будем иметь . Это означает, что через проходит по меньшей мере два решения 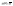уравнения (16). Между тем, в силу свойств функции правая часть уравнения удовлетворяет условиям теоремы о существовании и единственности решений ОДУ (обыкновенных дифференциальных уравнений). Из сказанного можно сделать вывод, что - монотонно возрастающая ограниченная функция. Тогда, по теореме Вейерштрасса, существует предел , который мы обозначим через . Покажем, что . В силу (16)

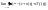
В то же время, непосредственное существование такого предела следует, что он равен нулю. В этом можно в частности убедиться, используя формулу конечных приращений. Таким образом, , то есть наряду с является корнем уравнения (20). Но как было установлено в предыдущем параграфе, это уравнение имеет в области единственное решение. Следовательно, 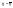, то есть выполняется соотношение (22).

Аналогично доказывается, что если ,то является монотонно убывающей функцией и имеет место соотношение (22).

Наконец, если 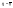, то 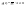, и соотношение (22) опять-таки справедливо.

Поведение траектории уравнения (16) при фиксированном постоянном , изображены на ДВА.

Из полученных результатов также следует, что постоянное решение уравнения (16) является устойчивым по Ляпунову, а значит и асимптотически устойчивым. Отметим, что доказано более сильное свойство, чем асимптотическая устойчивость. Так как последнее означает сходимость к тех траекторий, начальные значения которых достаточно близки к (глобальная асимптотическая устойчивость).

В заключение рассмотрим случай, когда производственная функция является функцией Кобба-Дугласа (см пар 1.9). В этом случае . Тогда (16) будет иметь вид (23)

Непосредственной проверкой можно убедиться в том, что общее решение этого уравнения представимо в виде (24)

Легко видеть, что 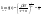, где - отвечающее сбалансированному росту значение фондовооруженности, являющееся корнем конечного уравнения .

Этот результат естественно совпадает с полученным выше результатом для произвольной линейной однородной производственной функции.