
- •1. Действующие лица экономики и их цели
- •1º Производители и потребители.
- •2º Цели потребителя.
- •3º Цели производителя.
- •3. Факторы производства
- •4. Закон убывающей доходности
- •12. Механизм прямого управления.
- •5. Модели экономических систем
- •6. Рынок, деньги и цены.
- •7. Спрос.
- •8. Предложение.
- •20. Денежная масса, номинальная и реальная заработная плата
- •9. Рынок как автоматический регулятор.
- •Равновесие спроса и предложения в условиях совершенной конкуренции
- •2. Воспроизводство.
- •10. Оценка роли рыночной системы.
- •11. Роль государства в регулируемой децентрализованной экономике.
- •13. Международная торговля и системы валютных курсов
- •14. Таможенные барьеры
- •36. Сравнительная статика модели Кейнса. Изменение предложения денег.
- •15. Макро- и микротеория. Агрегирование
- •16. Износ. Амортизация и инвестиции
- •19. Ценные бумаги
- •Облигации
- •17. Измерение объема национального производства и национального дохода
- •18. Сбережения и норма процента. Дисконтирование
- •21. Производственная функция
- •24. Классическая теория. Рынок капитала (сбережений и инвестиций)
- •Предложение капитала
- •Спрос на капитал
- •Равновесие на рынке капитала
- •23. Классическая теория. Рынок труда
- •Предложение труда
- •Спрос на труд
- •Равновесие на рынке труда
- •22. Макроэкономические теории
- •25. Классическая теория. Денежный рынок
- •26. Краткий обзор классической теории
- •27. Сравнительная статика
- •28. Критика классической теории
- •29. Теория Кейнса. Склонность к потреблению
- •Спекулятивный спрос на деньги
- •31. Теория Кейнса. Рынок труда
- •35. Теория Кейнса. Инфляция и безработица
- •32. Теория Кейнса. Рынок капитала (сбережений и инвестиций)
- •33. Краткая формулировка модели Кейнса и определение равновесия
- •34. Существование и единственность равновесия в модели Кейнса
- •42. Сравнительная статика модели Кейнса. Фискальная политика.
- •37. Сравнительная статика в модели Кейнса. Изменение функций инвестирования (I) и сбережения (s).
- •39. Сравнительная статика модели Кейнса. Изменение номинальной зарплаты
- •38. Сравнительная статика модели Кейнса. Изменение производственной функции.
- •40. Роль государства в модели Кейнса
- •41. Мультипликатор Кейнса
- •43. Критика теории Кейнса. Понятие о монетаризме.
- •44. Макроэкономическая динамика и воспроизводство
- •45. Экономические циклы.
- •46. Стабильное население
- •47. Стабилизация населения
- •Влияние нтп на возникновение экономических циклов
- •48. Демографический переход и демографический взрыв. Теория Мальтуса
- •49. Однопродуктовая макроэкономическая модель
- •50. Независимость производственного процесса от масштаба
- •51. Модель Солоу
- •52. Сбалансированный рост
- •53. Асимптотическое поведение траектории в модели Солоу
- •54. Моделирование запаздывания при освоении капиталовложений
- •55. Сбалансированный рост в однопродуктовой макродинамической модели с запаздыванием
- •57. Рост и нтп
- •59. Отношение предпочтения и функция полезности
- •56. Оптимальная норма накопления
- •58. Была ли необходима перестройка экономики в ссср?
- •60. Неоклассическая задача потребления
- •63. Задача максимизации прибыли фирмы в условиях совершенной конкуренции
- •61. Ценовая эластичность спроса.
- •62. Производственная функция фирмы
- •64. Несовершенная конкуренция. Монополия и монопсония
- •65. Конкуренция среди немногих. Олигополия, олигопсония
- •Список основных макроэкономических элементов
51. Модель Солоу
Для математического исследования динамической модели, построенной в §1, перейдем к относительным переменным
 (11)
(11)
Производительность
труда
 и фондовооруженность
и фондовооруженность
 были введены в рассмотрение в предыдущем
пункте. Величина
были введены в рассмотрение в предыдущем
пункте. Величина
 есть потребление на одного рабочего.
Ее называют удельным потреблением.
Если считать, что величина потребления
есть потребление на одного рабочего.
Ее называют удельным потреблением.
Если считать, что величина потребления
 полностью совпадает (в денежном
выражении) с общей массой зарплаты, то
полностью совпадает (в денежном
выражении) с общей массой зарплаты, то
 совпадает с
совпадает с
 .
Величина
.
Величина
 представляет собой долю произведенного
продукта, вкладываемую в расширение
производства, и называется нормой
(долей) накопления. Как отмечалось в
§1, для замыкания однопродуктовой
динамической модели надо в частности
задать закон изменения численности
занятых
представляет собой долю произведенного
продукта, вкладываемую в расширение
производства, и называется нормой
(долей) накопления. Как отмечалось в
§1, для замыкания однопродуктовой
динамической модели надо в частности
задать закон изменения численности
занятых
 .
Сейчас мы обсудим один из возможных
вариантов.
.
Сейчас мы обсудим один из возможных
вариантов.
На семинарских занятиях мы выяснили, что при отсутствии воин, эпидемий, притока или оттока беженцев и других потрясений население с течением времени стабилизируется. Сделав такое допущение, можно считать, что численность населения изменяется с постоянным темпом, т.е. по экспоненциальному закону. То же самое можно сказать и о численности активного населения, поскольку оно составляет фиксированную долю от численности населения в трудоспособном возрасте.
Предположим,
что экономика развивается в условиях
полной занятости или с постоянным
уровнем безработицы (с постоянным
процентом безработных). Тогда и
численность занятых
 будет изменяться с постоянным темпом.
будет изменяться с постоянным темпом.
Под
темпом роста непрерывной величины
понимают
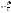 (12).
(12).
Если
 ,
,
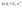
В
дальнейшем будем считать, что речь идет
о росте в буквальном понимании этого
слова, т.е.
 .
В силу (4), уравнение (2) может быть записано
в следующем виде:
.
В силу (4), уравнение (2) может быть записано
в следующем виде:
 (13)
(13)
Отсюда
и из (11) следует
 .
.
Разделив
обе части этого равенства на
 ,
с учетом (12) будем иметь
,
с учетом (12) будем иметь
 .
Используя формулу (8) приходим к
дифференциальному уравнению, которое
называют моделью Солоу:
.
Используя формулу (8) приходим к
дифференциальному уравнению, которое
называют моделью Солоу:
 (14)
(14)
Как
видно из формул (4) и (11),
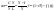 (15)
(15)
С
учетом этого уравнения получим
 (16).
(16).
Дифференциальное уравнение первого порядка относительно фондовооруженности.
Если
задана норма накопления
 ,
то по решению
,
то по решению
 уравнения (16) можно легко найти
макропеременные
уравнения (16) можно легко найти
макропеременные
 .
Действительно, если
.
Действительно, если
 ,
то
,
то
 .
.
Вычислив
по формулам (8-15)
 ,
можно получить и остальные макропеременные:
,
можно получить и остальные макропеременные:
 ,
,
 ,
,
 .
.
52. Сбалансированный рост
Под
сбалансированным ростом понимается
такой процесс экономического развития,
при котором основные макропоказатели
растут с постоянным
темпом. Применительно к рассмотренной
модели, это означает, что с постоянным
темпом должны возрастать величины
 .
При сделанном в предыдущем параграфе
предположении, будет обладать таким
свойством: обозначим
.
При сделанном в предыдущем параграфе
предположении, будет обладать таким
свойством: обозначим
 – темпы роста первых четырех показателей,
и сохраним принятое обозначение
– темпы роста первых четырех показателей,
и сохраним принятое обозначение
 для темпа роста рабочей силы. Тогда
для темпа роста рабочей силы. Тогда
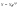 ,
,
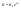 ,
,
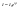 ,
,
 ,
,
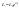 (17)
(17)
Покажем,
что в этом случае темпы роста всех
показателей должны совпадать. В силу
(2) и (17) имеем:
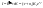 .
Отсюда, учитывая, что
.
Отсюда, учитывая, что
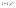 ,
получаем
,
получаем
 .
Из (13) и (17):
.
Из (13) и (17):
 (18)
(18)
Разделив
обе части этого тождества на
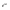 будем иметь
будем иметь

После дифференцирования по времени получаем
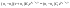 .
Это тождество при
.
Это тождество при
 ,
что эквивалентно
,
что эквивалентно
 .
(
.
( ).
).
Отсюда
и из (18) получаем
 ,
что может иметь место лишь в случае
,
что может иметь место лишь в случае
 .
.
Сопоставляя
полученные соотношения между темпами
роста, приходим к выводу, что
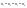 .
Покажем, что все эти величины равны
.
Покажем, что все эти величины равны
 - темпу роста рабочей силы. Поскольку
величины
- темпу роста рабочей силы. Поскольку
величины
 связаны производственной функцией, то
связаны производственной функцией, то
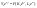 .
Используя линейную однородность
производственной функции, получаем
.
Используя линейную однородность
производственной функции, получаем
 .
Т.к.
.
Т.к.
 ,
то отсюда следует
,
то отсюда следует
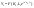 .
.
Производственная
функция монотонно возрастает по каждому
аргументу, поэтому полученное тождество
может выполняться лишь в том случае,
когда
 есть константа, т.е.
есть константа, т.е.
 .
Таким образом,
.
Таким образом,
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Итак,
при сбалансированном росте темпы
изменения основных макропоказателей
должны быть одинаковы. Отсюда, в
частности, следует, что при сбалансированном
росте норма накопления
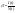 и фондовооруженность
и фондовооруженность
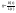 не зависят от времени. Это означает,
что траектории сбалансированного роста
отвечает решение дифференциального
уравнения Солоу (16), имеющее вид
не зависят от времени. Это означает,
что траектории сбалансированного роста
отвечает решение дифференциального
уравнения Солоу (16), имеющее вид
 .
Найдя такое решение, можно легко
определить основные макропеременные:
.
Найдя такое решение, можно легко
определить основные макропеременные:
 (19)
(19)
Покажем, что рассматриваемые модели для каждой фиксированной постоянной нормы накопления существует единственная траектория сбалансированного роста.
Постоянное
решения дифференциального уравнения
(16), соответствующее сбалансированному
росту, обращает левую часть этого
уравнения в нуль, то есть является
корнем следующего конечного
уравнения:
 (20)
(20)
Покажем,
что при заданном постоянном значении
нормы накопления
 уравнение (20) имеет в области
уравнение (20) имеет в области
 (только такие значения имеют экономический
смысл) единственное решение. Для этого
исследуем свойства функции
(только такие значения имеют экономический
смысл) единственное решение. Для этого
исследуем свойства функции
 (21)
(21)
Поскольку
 (см § 2), то
(см § 2), то
 .
В силу (10) имеем
.
В силу (10) имеем
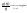
Отсюда,
в частности, следует, что в некоторой
правосторонней окрестности нуля
 функция
функция
 принимает положительные значения.
принимает положительные значения.
Далее,
из (9) следует
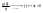 .
Тогда
.
Тогда
 при достаточно больших
при достаточно больших
 .
Сопоставляя полученные результаты,
приходим к тому, что в некоторой точке
.
Сопоставляя полученные результаты,
приходим к тому, что в некоторой точке
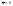 функция
функция
 обращается в ноль. Осталось доказать
единственность.
обращается в ноль. Осталось доказать
единственность.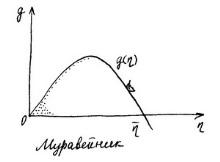
Поскольку
 (см пар 2), то и
(см пар 2), то и
 ,
то есть
,
то есть
 - строго вогнутая функция. Тогда, как
легко убедиться, она не будет иметь
положительных нулей, отличных от
- строго вогнутая функция. Тогда, как
легко убедиться, она не будет иметь
положительных нулей, отличных от
 .
Возможный график этой функции приведен
на рисунке «Муравейник».
.
Возможный график этой функции приведен
на рисунке «Муравейник».
Итак,
при фиксированной постоянной норме
накопления уравнение (20) имеет в области
 единственное решение, т.е. в рассматриваемой
модели существует единственная
траектория сбалансированного роста
при каждом
единственное решение, т.е. в рассматриваемой
модели существует единственная
траектория сбалансированного роста
при каждом
 .
.
Замечание.
Легко видеть, что чем больше норма
накопления, тем больше фондовооруженность
 на траектории сбалансированного роста.
на траектории сбалансированного роста.
