14. Расчет на прочность при ударном действии нагрузок Удар. Основные понятия

Явление удара наблюдается во всех случаях, когда скорости соприкасающихся тел изменяются в течение очень малого промежутка времени.

Напряжения и деформации при ударном нагружении, называемые динамическими, оказываются значительно большими, чем те, которые возникли бы в данной системе при статическом приложении той же нагрузки.

Процесс удара жесткого груза об упругую стержневую систему протекает следующим образом. Сначала груз, движущийся с некоторой скоростью, входит в соприкосновение с системой, причем скорость его движения резко уменьшается.

Упругая система приходит в движение. Однако вследствие инерции массы системы ее частицы начинают перемещаться не одновременно. Чтобы волна деформации распространилась от места удара по всей системе, требуется некоторое время. Передний фронт волны движется по системе со скоростью распространения звука в данной среде. В стальных конструкциях, например, волна деформации распространяется со скоростью около 5000 м/с.

После соприкосновения груз движется совместно с воспринимающей удар упругой системой, причем скорость их движения по мере роста деформаций и сил упругости системы постепенно уменьшается и становится равной нулю в момент наибольшей деформации. Затем начинается обратное движение, в дальнейшем система совершает колебательные движения.

Расчет на прочность и жесткость при ударной нагрузке требует определения напряжений и деформаций системы, воспринимающей удар.

При назначении динамических допускаемых напряжений следует учитывать изменение механических характеристик материала. Однако ввиду недостаточной изученности этого вопроса расчет на прочность при динамической нагрузке обычно ведут по статическим характеристикам, то есть условие прочности имеет следующий вид:

.

(15.1)

При ударе возникают деформации двух типов: местные деформации в зоне контакта и общие деформации системы. В дальнейшем рассматриваются только общие деформации системы, и предполагается, что динамические напряжения не превосходят предел пропорциональности материала. Задача определения контактных напряжений в месте удара сложна и не может быть решена простыми методами.

Для приближенного определения напряжений и перемещений сечений в момент наибольшей деформации системы в практических расчетах обычно применяется энергетический метод. Этот метод решения применим в тех случаях, когда скорость ударяющего тела мала по сравнению со скоростью распространения фронта ударной волны, а время соударения значительно больше времени распространения этой волны по всей системе.

Указанное ограничение дает основание считать, что при ударе деформации распространяются мгновенно по всей стержневой системе и все ее точки начинают движение одновременно.

Под ударной понимается всякая быстроизменяющаяся нагрузка.При ударном действии нагрузки различные точки системы получают некоторые скорости, так что системе придается кинетическая энергия, которая переходит в потенциальную энергию деформации конструкции, а также в другие виды энергии – прежде всего в тепловую. При ударе развивается склонность к хрупкому разрушению, особенно при пониженных температурах и больших напрягаемых объемах. Характеристикой склонности материала к хрупкому разрушению является удельная ударная вязкость a_k. Для ее определения образец подвергают ударным испытаниям на маятниковом копре.

Простейшая теория удара основана на следующих допущениях:

1. Удар считается неупругим, то есть ударяющее тело продолжает двигаться вместе с ударяемой конструкцией, не отрываясь от нее. Иными словами ударяющее тело и ударяемая конструкция имеют общие скорости после удара.

2. Ударяемая конструкция имеет лишь одну степень свободы, и вся масса конструкции сосредоточена в точке удара.

3. Рассеянием энергии в момент удара пренебрегаем, считая, что вся кинетическая энергия ударяющего тела переходит в потенциальную энергию деформации ударяемой конструкции, движение которой происходит при отсутствии сил сопротивления.

4. Ударяемая конструкция считается идеально упругой.

Это означает, что зависимость между динамическими усилиями и перемещениями, ими вызванными, точно так же подчиняется закону Гука, как и при статическом действии нагрузок (рисунок 15.1).

Назовем отношение динамических и статических перемещений коэфициентом динамичности или динамическим коэффициентом:

.

(15.2)

В соответствии с законом Гука, имеем

,

(15.3)

где σ_д - динамические напряжения; σ_ст - статические напряжения.

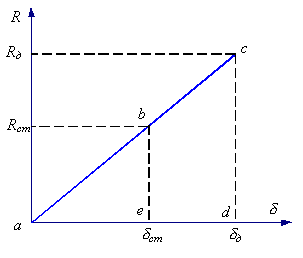
Рисунок 15.1.