Пример 12.1

Решить плоскую раму, представленную на рисунок 12.7.

Данная рама дважды статически неопределима. На рисунок 12.7 показаны три из большого числа возможных эквивалентных систем. Остановимся на первой системе и запишем для нее канонические уравнения

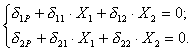
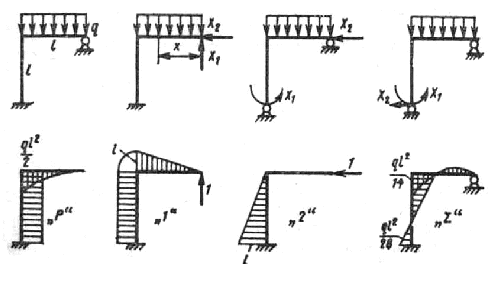
Рисунок 12.7.

Коэффициенты этих уравнений вычислим способом Верещагина. Для этого построим эпюры изгибающих моментов от распределенной нагрузки и единичных сил. Перемножая эпюры согласно индексам коэффициентов, находим

Подставляя эти значения коэффициентов в канонические уравнения и решая их, получаем

.

Суммируя ординаты эпюры «P» с ординатами эпюры «1», умноженными на , и эпюры «2», увеличенными в раз, строим суммарную эпюру изгибающих моментов M_Σ.

Изгибающий момент в текущем сечении горизонтального участка находим по формуле (12.8):

.

Приравнивая нулю производную , устанавливаем, что эта функция имеет экстремум при , причем .

Пример 12.2

Построить эпюру изгибающих моментов для рамы, представленной на рисунок 12.8.

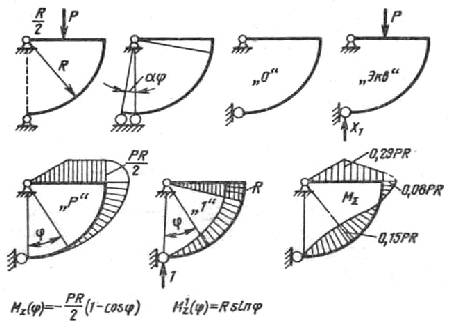
Рисунок 12.8.

Рама один раз статически неопределима. Выберем основную систему, удаляя одну связь в нижнем (или верхнем) шарнире. Однако в рассматриваемой раме горизонтальные и вертикальные опорные связи неравноценны. Если удалить горизонтальную связь, то при любой нагрузке реакция R_y оставшейся вертикальной вязи должна быть бесконечно большой, так как линия ее действия проходит через центр верхнего шарнира, а момент внешней нагрузки относительно этого шарнира не равен нулю. Чтобы воспринять даже самую малую нагрузку, эта рама должна сначала повернуться как жесткое целое (без деформации) на бесконечно малый угол dφ. Тогда плечо реакции R_y станет отличным от нуля, а сама реакция будет конечной, но значительной по величине.

Такая система является мгновенно геометрически изменяемой. Ее в качестве основной системы выбирать нельзя.

Положение сразу же изменяется, если удалить не горизонтальную, а вертикальную опорную связь. В такой основной системе при любой нагрузке опорные реакции и внутренние силовые факторы будут конечными и определенными. Эквивалентная система, соответствующая этой основной системе, представлена на рисунок 12.8. Там же приведены эпюры изгибающих моментов от заданной и единичных нагрузок.

Вычисляя коэффициенты канонического уравнения δ_1P+δ₁₁X₁=0 интегрированием на криволинейных участках и перемножением эпюр на прямолинейных, получаем

;

.

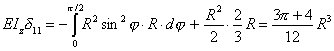Отсюда

.

Суммарный изгибающий момент на криволинейном участке изменяется по закону

.

Приравнивая нулю производную от M_Σ(φ):

,

получаем

.

Следовательно, при φ=40° функция M_Σ(φ) имеет экстремум, причем M_Σ(45°)=0.15PR. Суммарная эпюра приведе на на рисунок 12.8.

Определение перемещений в статически неопределимых системах

После раскрытия статической неопределимости и построения суммарных эпюр силовых факторов можно приступить к определению перемещений сечений рассматриваемой стержневой системы. Естественно это делать методом Мора, перемножая, где возможно, по правилу Верещагина суммарные эпюры внутренних силовых факторов на соответствующие эпюры от единичных нагрузок, приложенных в сечениях, перемещения которых определяются.

Однако построение эпюр от единичных нагрузок при приложении их непосредственно к заданной системе требует вторичного раскрытия ее статической неопределимости. Такой достаточно трудоемкой операции можно избежать, если определять перемещения не в заданной, а в эквивалентной системе. Причем не обязательно пользоваться первоначальной эквивалентной системой, выбранной для раскрытия статической неопределимости, так как перемещения одного и того же сечения во всех системах, эквивалентных данной, одинаковы.

Если сечение заданной системы в рассматриваемом направлении не перемещается, то произведение суммарной эпюры на единичную должно быть равно нулю. На этом свойстве основана проверка правильности вычисления неизвестных X₁, X₂, X₃,...X_n при раскрытии статической неопределимости и построения суммарных эпюр.

Абсолютные или относительные перемещения сечений в направлении усилий X₁, X₂, X₃,...X_n отсутствуют, поэтому произведение каждой из единичных эпюр на суммарную должно быть обязательно равно нулю. Пользуясь этим правилом, нетрудно проверить, что суммарная эпюра изгибающих моментов в примере 12.1 построена правильно, так как произведение этой эпюры на первую единичную (см. рисунок 12.7)

.

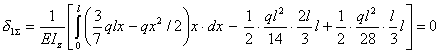Ордината суммарной эпюры, под центром тяжести второй единичной эпюры, как видно из рисунка 12.7, равна нулю. Следовательно, произведение и этих двух линейных эпюр также равно нулю.