Расчеты на прочность и жесткость при кручении

Принципы расчетов на прочность, изложенные в главе 4 применительно к одноосному растяжению и сжатию, полностью справедливы и для случая кручения бруса. При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности

(7.34)

где τ_max - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое касательное напряжение, равное части предельного напряжения для материала детали - предела прочности τ_в или предела текучести τ_т. Коэффициент запаса прочности устанавливается из тех же соображений, что и при растяжении. Например, для вала полого круглого поперечного сечения, с внешним диаметром D и внутренним диаметром d, имеем

,

(7.35)

где α=d/D - коэффициент полости сечения.

Условие жесткости такого вала при кручении имеет следующий вид:

,

(7.36)

где [φ_o] - допускаемый относительный угол закручивания.

 

Пример 7.2

Подобрать диаметр сплошного вала, передающего мощность N=450 л.с. при частоте вращения n=300 об/мин. Угол закручивания не должен превышать одного градуса на 2 метра длины вала; [τ]=40 МПа, G=8·10⁴ МПа.

Крутящий момент определяем из уравнения (7.1)

Диаметр вала по условию прочности определяется из уравнения (7.35)

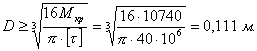
Диаметр вала по условию жесткости определяется из уравнения (7.36)

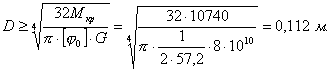
Выбираем больший размер 0,112 м.

Пример 7.3

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающих одинаковый крутящий момент; один из них сплошной, а другой полый с коэффициентом полости α=0.8. Во сколько раз сплошной вал тяжелее полого?

Равнопрочными валами из одинакового материала считаются такие валы, у которых при одинаковых крутящих моментах, возникают одинаковые максимальные касательные напряжения, то есть

.

Условие равной прочности переходит в условие равенства моментов сопротивления:

.

Откуда получаем:

.

Отношение весов двух валов равно отношению площадей их поперечных сечений:

.

Подставляя в это уравнение отношение диаметров из условия равной прочности, получим

.

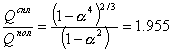Как показывает этот результат, полый вал, будучи одинаковым по прочности, вдвое легче сплошного. Это объясняется тем, что в силу линейного закона распределения касательных напряжений по радиусу вала, внутренние слои относительно мало нагружены.

Пример 7.4

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающие одинаковый крутящий момент; один из них круглого поперечного сечения, а другой - квадратного. Во сколько раз квадратный вал тяжелее круглого?

Условие равной прочности имеет следующий вид:

,

где W_к=αhb²; значение коэффициента α определяется по таблице 7.1 и составляет для квадратного сечения (b=h) α=0.208.

Из условия равной прочности получаем:

.

Отношение весов двух валов равно отношению площадей их поперечных сечений:

.

Подставляя в это уравнение отношение b/D из условия равной прочности, получим

.

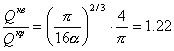Расчет цилиндрических винтовых пружин малого шага

Определим напряжения и деформации при осевом растяжении и сжатии цилиндрической пружины, навитой из прутка круглого сечения диаметра d (рисунок 7.18 а). Конструктивно пружины растяжения и сжатия отличаются оформлением их концов, но концевые витки при расчетах пружин на прочность и жесткость во внимание не принимаются.

Цилиндрические пружины характеризуются средним диаметром витка D, числом витков n, углом подъема витков α и шагом пружины h.

Наибольшее распространение в технике имеют пружины с небольшим углом подъема винтовой линии (α<5°), называемые пружинами малого шага.

В пружинах малого шага можно пренебречь подъемом витков и считать длину витка примерно равной πD, а сам виток - расположенным в плоскости, нормальной к оси пружины. Но в таком случае, сечение прутка пружины плоскостью, содержащей ее ось, можно рассматривать как ее поперечное сечение. Указанные допущения положены в основу приближенного расчета пружин.

Разделим пружину осевым сечением на две части и отбросим, одну из них. Из условия равновесия оставшейся части (рисунок 7.18 б) следует, что внутренние касательные силы упругости в сечении пружины приводятся к перерезывающей силе Q=P и крутящему моменту М_к=PD/2.

Касательные напряжения, вызванные кручением, достигают максимума в контурных точках сечения, а напряжения от перерезывающей силы можно в первом приближении считать равномерно распределенными по плоскости сечения. В точке А контура сечения суммарные касательные напряжения, как видно из рисунок 7.19, достигают наибольшей величины

,

или

.

(7.37)

Для большинства пружин отношение d/2D - величина малая по сравнению с единицей. Это говорит о том, что основным видом деформации для пружин является кручение, а срезом можно пренебречь и вычислять напряжения в пружине по формуле

.

(7.38)

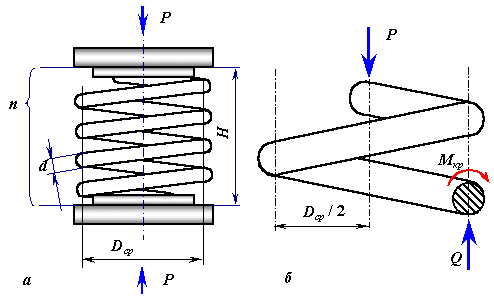
Рисунок 7.18

Рисунок 7.19

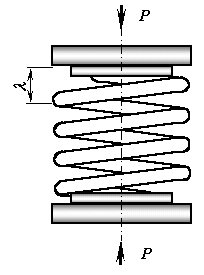
Рисунок 7.20

Изменение продольных размеров λ (рисунок 7.20) удобно определить энергетическим методом, приравнивая работу А статически приложенной силы Р потенциальной энергии деформации U пружины. Работа внешних сил A=Pλ/2, а потенциальная энергия накапливается, главным образом, за счет кручения прутка и поэтому может быть вычислена по формуле (7.15). Учитывая, что крутящий М_к=PD/2 и момент инерции I_p=πd⁴/32 по длине прутка не изменяются, а длина прутка l = πdn, получаем

.

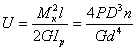Приравнивая A и U, находим

.

(7.39)

Для пружин сжатия формула (7.39) справедлива лишь до полного обжатия пружины, т. е. до соприкосновения ее витков. После полного обжатия пружина начинает работать на осевое сжатие как прямой пустотелый брус.
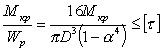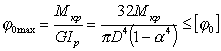