Анализ напряженного состояния при растяжении (сжатии)

При растяжении бруса наклонные сечения, как и поперечные, остаются плоскими и параллельными. Следовательно, внутренние силы распределены по наклонным сечениям равномерно.

Нормальное напряжение в поперечном сечении растянутого или сжатого стержня есть главное напряжение. Поэтому на рисунок 4.20 оно обозначено s₁. Так как отлично от нуля только одно главное напряжение, то напряженное состояние при одноосном растяжении (сжатии) является линейным. При растяжении:

,

при сжатии:

.

Составляющие вектора полного напряжения по координатным осям в наклонной площадке определяются из уравнения (3.9) или (3.10):

,

Нормальные и касательные напряжения в наклонной площадке – по уравнениям (3.12), (3.13). Для случая растяжения стержня:

,

На площадке, наклоненной под углом β=π/2+α:

,

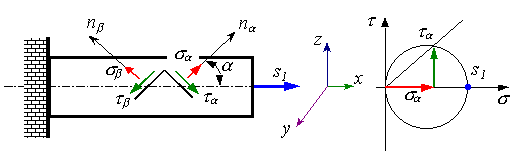
Рисунок 4.20. Напряжения на наклонных площадках

На 4.20 показаны напряжения на наклонных площадках и построен круг Мора для случая растяжения стержня. Аналогичные построения и расчеты могут быть сделаны и для случая сжатия стержня. Таким образом, напряжения в стержне изменяются в зависимости от наклона сечения. Тем самым на конкретном примере подтверждается зависимость напряжений в точке тела от ориентировки площадки их действия. Анализ формул показывает, что при одноосном растяжении бруса нормальные напряжения достигают наибольших значений в поперечных сечениях (α=0), а касательные напряжения τ_α - в сечении, наклонном к оси бруса под углом α=45°, причем τ_max=s₁/2. В продольном сечении (α=90°) касательные и нормальные напряжения равны нулю.

Интересно отметить, что сумма нормальных напряжений на двух любых ортогональных площадках есть величина постоянная, а касательные напряжения на этих площадках равны по величине, что является проявлением сформулированного выше закона парности касательных напряжений.

Потенциальная энергия деформации при растяжении

Внешние силы в процессе деформации тела производят работу. Часть затраченной на деформацию энергии поглощается телом и накапливается в нем в виде потенциальной энергии, называемой потенциальной энергией деформации. Остальная часть расходуется на необратимые процессы - нагрев тела, изменение его электромагнитных свойств и т. д. Соотношение между этими двумя слагаемыми энергии внешних сил изменяется в процессе нагружения тела.

В пределах упругих деформаций затрата энергии на необратимые процессы весьма незначительна, и поэтому можно считать, что в пределах упругости работа внешних сил полностью переходит в потенциальную энергию деформации. Таким образом, упругое тело является как бы аккумулятором энергии.

За пределами упругости большая часть работы внешних сил затрачивается на необратимые процессы, а при разгрузке выделяется лишь часть энергии, связанная с упругими деформациями тела.

При разгрузке идеально упругого тела накопленная в нем потенциальная энергия полностью расходуется на восстановление его первоначальной формы и размеров, причем эту работу производят внутренние силы. Следовательно, потенциальная энергия деформации равна работе внутренних сил упругости на перемещениях точек их приложения, и поэтому всегда может быть выражена через эти силы. Формула (3.44) дает возможность определить удельную потенциальную энергию деформации в общем случае объемного напряженного состояния. В частном случае линейного растяжения, имеем:

.

(4.14)

Потенциальная энергия деформации U определится из уравнения (4.15) путем интегрирования по объему:

.

(4.15)

Например, в брусе постоянного сечения при действии постоянной по длине силы P, имеем

.

(4.16)
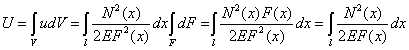