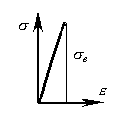- •Бийский технологический институт (филиал)
- •170104.65 – Высокоэнергетические устройства
- •160302.65 - Ракетные двигатели
- •Оглавление
- •Введение
- •Принципы сопротивления материалов Принцип Сен-Венана
- •Принцип независимости действия сил
- •Принцип начальных размеров
- •Внутренние силы. Метод сечений
- •Напряжения и деформации Напряжения
- •Связь компонентов внутренних сил с напряжениями
- •Определение напряжений на наклонных площадках
- •Определение главных напряжений и главных площадок
- •Плоское напряженное состояние
- •Графический способ определения напряжений Круги Мора
- •Графическое определение главных напряжений и положения главных площадок
- •Деформации. Деформированное состояние в точке тела
- •Обобщенный закон Гука для изотропного тела
- •Удельная потенциальная энергия деформации
- •Пример 3.1
- •Растяжение-сжатие Определение внутренних усилий
- •Определение напряжений
- •Определение деформаций и перемещений
- •Определение механических свойств материала при растяжении
- •Диаграммы условных и истинных напряжений
- •Механические характеристики материалов
- •Закон разгрузки и повторного нагружения
- •Пластичные и хрупкие материалы
- •Механические свойства при сжатии
- •Влияние температуры на механические характеристики
- •Ползучесть, последействие и релаксация
- •Длительная прочность
- •Коэффициент запаса прочности. Выбор допускаемых напряжений
- •Основные типы задач при расчете на прочность растянутых (сжатых) стержней
- •Пример 4.1
- •Пример 4.2
- •Пример 4.3
- •Анализ напряженного состояния при растяжении (сжатии)
- •Потенциальная энергия деформации при растяжении
- •Концентрация напряжений
- •Статически неопределимые задачи при растяжении и сжатии
- •Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Сдвиг (срез) Определение внутренних сил, напряжений и деформаций при сдвиге
- •Анализ напряженного состояния при сдвиге
- •Потенциальная энергия деформации при чистом сдвиге
- •Расчет на прочность при сдвиге
- •Расчет заклепочного соединения
- •Пример 5.1
- •Геометрические характеристики плоских сечений
- •Определения
- •Зависимость между моментами инерции относительно параллельных осей
- •Моменты инерции простейших фигур
- •Вычисление моментов инерции сложных фигур
- •Изменение моментов инерции при повороте осей координат
- •Главные оси и главные моменты инерции
- •Моменты сопротивления площади
- •Пример 6.1
- •Кручение Внутренние силовые факторы при кручении
- •Напряжения и деформации при кручении бруса круглого поперечного сечения
- •Напряженное состояние при кручении
- •Потенциальная энергия деформации при кручении
- •Направление вектора касательного напряжения в контурных точках сечения цилиндрического бруса
- •Кручение тонкостенного бруса замкнутого профиля
- •Кручение бруса прямоугольного сечения
- •Кручение тонкостенного бруса открытого профиля
- •Пример 7.1
- •Расчеты на прочность и жесткость при кручении
- •Пример 7.2
- •Пример 7.3
- •Пример 7.4
- •Расчет цилиндрических винтовых пружин малого шага
- •Статически неопределимые задачи при кручении
- •Плоский прямой поперечный изгиб Основные понятия и определения
- •Плоский прямой изгиб
- •Нормальные напряжения при чистом прямом изгибе
- •Касательные напряжения при плоском прямом изгибе. Формула Журавского
- •Пример 8.1
- •Пример 8.2
- •Расчеты на прочность при поперечном изгибе
- •Потенциальная энергия деформации при изгибе
- •Перемещения при изгибе Дифференциальное уравнение упругой линии балки и его интегрирование
- •Пример 8.4
- •Пример 8.5
- •Пример 8.6
- •Расчет на жесткость при изгибе
- •Определение перемещений с помощью интеграла Мора
- •Пример 8.7
- •Определение перемещений с помощью способа Верещагина
- •Пример 8.9
- •Пример 8.10
- •Определение перемещений с помощью правила «дирижера»
- •Критерии предельного состояния материала при сложном напряженном состоянии. Теории прочности
- •Гипотезы (теории) прочности
- •Критерии разрушения
- •Гипотеза наибольших нормальных напряжений (I теория прочности)
- •Гипотеза наибольших линейных деформаций (II теория прочности)
- •Критерии пластичности
- •Гипотеза наибольших касательных напряжений (III теория прочности)
- •Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности)
- •Теория прочности Мора (V теория прочности)
- •Замечания о выборе теории прочности
- •Пример 9.1
- •Пример 9.2
- •Пример 9.3
- •Пример 9.4
- •Расчет на прочность при сложном сопротивлении
- •Косой (двойной) изгиб
- •Пример 10.1
- •Внецентренное растяжение (сжатие)
- •Пример 10.2
- •Пример 10.3
- •Изгиб с кручением
- •Общий случай сложного сопротивления
- •Перемещения в пространственном брусе малой кривизны при произвольной нагрузке
- •Пример 11.1
- •Пример 11.2
- •Статически неопределимые стержневые системы Статическая неопределимость
- •Метод сил. Канонические уравнения
- •Вычисление коэффициентов канонических уравнений
- •Пример 12.1
- •Пример 12.2
- •Определение перемещений в статически неопределимых системах
- •О рациональном выборе основной системы. Использование прямой и обратной симметрии
- •Пример 12.3
- •Пример 12.4
- •Пример 12.5
- •Пример 12.6
- •Устойчивость сжатых стержней. Продольный изгиб Понятие об устойчивости первоначальной формы равновесия
- •Определение критической силы. Формула Эйлера
- •Пределы применимости формулы Эйлера
- •Устойчивость сжатых стержней за пределами упругости. Полная диаграмма критических напряжений
- •Практические способы расчета на продольный изгиб
- •Пример 13.1
- •Расчет на устойчивость с помощью коэффициента снижения основного допускаемого напряжения
- •Рациональные формы сечений сжатых стержней
- •Пример 13.2
- •Расчет элементов конструкций, движущихся с ускорением Внутренние силы, вызванные движением. Силы инерции
- •Расчет поступательно движущихся систем
- •Напряжения в тонкостенном вращающемся кольце
- •Расчет равномерно вращающегося прямого бруса
- •Вращающиеся рамы
- •Расчет на прочность при ударном действии нагрузок Удар. Основные понятия
- •Вертикальный удар
- •Пример 15.1
- •Пример 15.2
- •Пример 15.3
- •Вертикальный удар вследствие внезапной остановки движения
- •Горизонтальный удар
- •Скручивающий удар
Закон разгрузки и повторного нагружения
Если образец нагрузить до напряжений, больших σу, но меньших σв, например до точки K диаграммы (Рисунок 4.6), а затем начать разгружать, то разгрузка будет происходить по прямой KL, параллельной начальному линейному участку диаграммы. После разгрузки деформация образца уменьшится, но полностью не исчезнет. Отрезок LM определяет величину исчезающей, т. е. упругой деформации εу, а отрезок OL - величину остаточной (пластической) деформации εпл. Прямолинейность линии разгрузки показывает, что упругая деформация подчиняется закону Гука и за пределами пропорциональности.
Повторное нагружение образца уже не повторяет полностью прежнюю диаграмму, а происходит сначала по прямой разгрузки KL, и затем по кривой КС, которую имел бы этот образец без промежуточной разгрузки. Следовательно, после промежуточной разгрузки появился как бы новый материал с более высоким пределом пропорциональности, но меньшей пластичностью.
Явление повышения упругих свойств материала в результате предварительного пластического деформирования называется наклепом или нагартовкой. Наклеп возникает при вытяжке, холодной прокатке металла, в процессе штамповки и т. д. Часто наклеп играет положительную роль и применяется для упрочнения поверхностного слоя детали, повышения упругости свойств проволоки, канатов и т. п. В тех случаях, когда наклеп вреден, его устраняют отжигом.
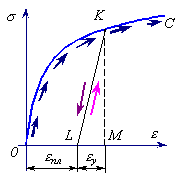
Рисунок 4.7. Закон упругой разгрузки
Пластичные и хрупкие материалы
По результатам испытаний на одноосное растяжение материалы принято делить на пластичные и хрупкие. К пластичным относятся материалы, разрушению которых предшествуют большие остаточные деформации, достигающие иногда 20...25%. Хрупкими называют материалы, разрушающиеся при малых остаточных деформациях, не превышающих 2...5%. Характерными представителями пластичных материалов являются малоуглеродистая сталь и алюминий, а хрупких - чугун, инструментальная сталь и стекло. Пластичные и хрупкие материалы отличаются еще и характером разрушения при растяжении. Пластичные материалы проявляют большее сопротивление отрыву частиц, чем сдвигу их друг относительно друга, (и разрушаются главным образом, от сдвига частиц в плоскостях действия наибольших касательных напряжений. Именно вследствие сдвига частиц увеличивается длина образца из пластичного материала при его растяжении, а место разрушения в шейке имеет вид кратера, стенки которого наклонены к оси образца под углом 45° (Рисунок 4.8). Дном этого кратера является поверхность первоначальной внутренней трещины, возникающей после образования шейки.
Хрупкие материалы, наоборот, обладают большим сопротивлением сдвигу, чем отрыву, и разрушаются при растяжении внезапно от отрыва частиц материала по плоскости поперечного сечения (Рисунок 4.9). Явления текучести, упрочнения и образования шейки на образцах из таких материалов перед разрывом не наблюдаются. Единственной прочностной характеристикой хрупких материалов является предел прочности σв. Диаграмма растяжения хрупких материалов представлена на Рисунок 4.10.
|
|
|
Рисунок 4.8 |
Рисунок 4.9 |
Рисунок 4.10 |
Деление материалов на хрупкие и пластичные является условным, так как свойства материалов зависят от температуры, скорости и вида нагружения. Один и тот же материал в одних условиях ведет себя как хрупкий, в других - как пластичный. Например, мрамор при одноосном растяжении разрушается как хрупкий материал, а при всестороннем сжатии проявляет пластические свойства. Поэтому правильнее говорить о пластичном и хрупком характере разрушения материала. Первое происходит при больших, а второе при сравнительно малых остаточных деформациях.