0. Вопросы для самоподготовки к лабораторной работе № 6

1. Аналитическая функция Кобба-Дугласа. Записать ее вид и разъяснить.

2. Способы расчета параметров , , производственной функции Кобба-Дугласа.

3. Средняя производительность труда. Расчет и экономическая интерпретация.

4. Средняя фондоотдача. Расчет и экономическая интерпретация.

5. Предельная производительность труда. Расчет и экономическая интерпретация.

6. Предельная фондоотдача. Расчет и экономическая интерпретация.

7. Эластичность выпуска продукции по затратам труда. Расчет и экономическая интерпретация.

8. Эластичность выпуска продукции по производственным фондам. Расчет и экономическая интерпретация.

9. Потребность в ресурсах труда . Расчет и экономическая интерпретация.

10. Потребность в производственных фондах . Расчет и экономическая интерпретация.

11. Фондовооруженность труда. Расчет и экономическая интерпретация.

12. Предельная норма замещения затрат труда производственными фондами . Расчет и экономическая интерпретация.

13. Эластичности замещения ресурсов. Расчет и экономическая интерпретация.

8. Лабораторная работа № 7. Системы эконометрических уравнений

8.1. Теоретические замечания. Ряд экономических процессов моделируется не одним, а несколькими эконометрическими уравнениями, содержащими как повторяющиеся, так и собственные переменные. В силу этого возникает необходимость использования систем эконометрических уравнений. Кроме того, в одних уравнениях определенная переменная рассматривается как объясняющая, а в другое уравнение она входит как зависимая переменная. Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений. Различают несколько видов систем.

Система эконометрических уравнений называется системой независимых уравнений, если в каждом уравнении зависимая переменная рассматривается как функция одного и того же набора факторов. В общем случае ее можно записать в виде:

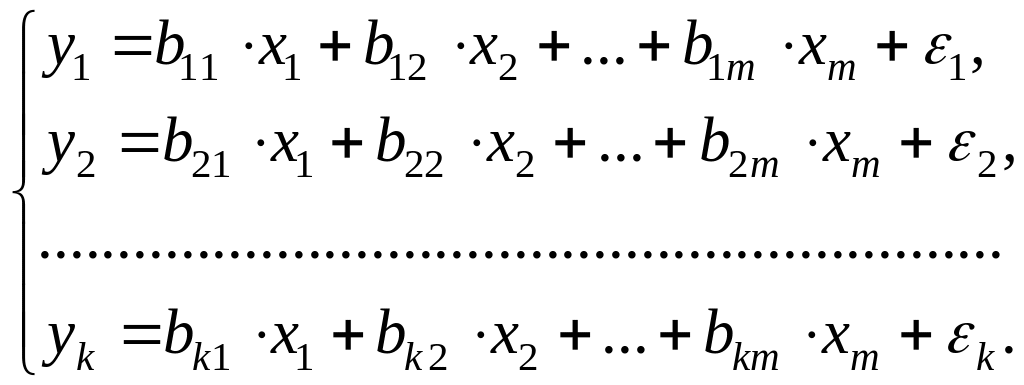(8.1)

Система эконометрических уравнений называется системой рекурсивных уравнений, если зависимая переменная одного уравнения является фактором в последующих уравнениях. В общем случае ее можно записать в виде:

(8.2)

Найти параметры систем (8.1), (8.2) можно с помощью МНК, применяя его последовательно к каждому уравнению системы.

Система эконометрических уравнений называется системой взаимосвязанных (одновременных) уравнений, если зависимые переменные уравнений является факторами в других уравнениях. В общем случае ее можно записать в виде:

(8.3)

Такая система уравнений называется структурной формой модели. Найти параметры таких систем можно с помощью косвенного или двухшагового МНК.

Эндогенными переменными называются переменные, которые определяются внутри системы. Экзогенными переменными называются переменные, которые определяются вне системы. Предопределенными переменными называются экзогенные и лаговые эндогенные переменные. Коэффициенты при переменных в структурной формой модели называются структурными.

Для определения структурных коэффициентов структурная форма модели преобразуется в приведённую форму. Система линейных функций эндогенных переменных от всех предопределенных переменных системы называется приведенной формой модели:

(8.4)

где - коэффициенты приведенной формы модели.

Проблема идентификации. При переходе от приведенной формы модели к структурной возникает проблема идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами моделей. С позиции идентифицируемости системы можно разделить на три вида:

• идентифицируемые;

• неидентифицируемые;

• сверхидентифицируемые.

Структурный коэффициент называется точно идентифицируемым, если его можно однозначно вычислить на основе приведенных коэффициентов; сверхидентифицируемым, если он имеет несколько разных оценок через приведенные коэффициенты; неидентифицируемым, если он не выражается через приведенные коэффициенты.

Точно идентифицируемый и сверхидентифицируемый коэффициент называют идентифицируемым.

Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируемый, то и всё уравнение является неидентифицируемым.

Модель считается идентифицируемой, если каждое её уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема.

Непосредственно проверять идентифицируемость сложно. Для этого надо устанавливать разрешимость нелинейной системы уравнений. Поэтому для определения идентифицируемости используют определенное правило, состоящее из необходимого и достаточного условия.

Необходимое условие идентифицируемости (условие порядка) уравнения. Пусть общее количество экзогенных переменных модели; количество экзогенных переменных, которые входят в е уравнение структурной формы модели, количество эндогенных переменных в -м уравнении структурной формы. Тогда имеет место необходимое условие идентифицируемости: если для го уравнения выполняется неравенство , то оно идентифицируемо.

Запишем это условие в виде

– уравнение точно идентифицируемо; (8.5)

– уравнение сверхидентифицируемо; (8.6)

– уравнение неидентифицируемо. (8.7)

Одни только необходимые условия не гарантируют идентифицируемость уравнения. Может случиться, что условие порядка для некоторого уравнения выполнено, а уравнение неидентифицируемо. Для уточнения вопроса идентифицируемости уравнения добавляют к необходимому условию ещё и достаточное.

Достаточное условие идентифицируемости (ранговое условие). Уравнение идентифицируемо, если ранг матрицы, составленной из коэффициентов при переменных во всех других уравнениях, кроме данного, отсутствующих в исследуемом уравнении, равен числу эндогенных переменных системы без единицы, т.е. .

Методы оценивания параметров структурной модели. Для оценки коэффициентов структурной модели применяются различные способы в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили:

• косвенный метод наименьших квадратов;

• метод инструментальных переменных;

• двухшаговый метод наименьших квадратов (2МНК);

• трехшаговый метод наименьших квадратов (3МНК).

Для оценки параметров идентифицируемых уравнений применяется косвенный метод наименьших квадратов, для сверхидентифицированных – двухшаговый МНК.

Косвенный МНК включает следующие этапы:

1. составляют приведенную форму модели;

2. оценивают параметры каждого уравнения приведенной формы с помощью МНК;

3. путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым оценки структурных параметров.

Двухшаговый МНК включает следующие этапы:

1. записывают общий вид приведенной формы модели;

2. оценивают параметры каждого уравнения приведенной формы с помощью МНК;

3. выявляют эндогенные переменные, находящиеся в правой части структурного уравнения и находят расчетные значения по полученным на втором этапе соответствующим уравнениям приведенной формы;

4. с помощью обычного МНК определяют параметры каждого структурного уравнения, в отдельности используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения, полученные на втором этапе.

8.2. Проверка идентифицируемости системы эконометрических уравнений. Рассматривается модель экономики страны:

			– функция потребления;
			– функция инвестиций;	(8.8)
		– функция денежного рынка;
	– тождество дохода.

Здесь:

– расходы на потребление в период ;

– совокупный доход в период ;

– инвестиции в период ;

– процентная ставка в период ;

– денежная масса в период ;

– государственные расходы в период ;

– расходы на потребление в период ;

– инвестиции в период ;

– случайные ошибки.

Для данной модели требуется:

1. предложить способ оценки параметров модели (предполагается, что имеются временные ряды по всем переменным модели);

2. как изменится ответ на вопрос п.1, если из модели исключить тождество дохода.

Решение. Модель представляет собой систему одновременных уравнений. Для определения способа оценок параметров модели проверим каждое уравнение на идентифицируемость.

Модель включает четыре эндогенные переменные , , , и четыре предопределенные переменные (две экзогенные переменные – , и две лаговые эндогенные переменные – , ), т.е. .

Проверим необходимое условие идентифицируемости уравнений исходной модели.

Первое уравнение включает две эндогенные переменные , и одну предопределённую . В этом уравнении присутствует одна предопределенная переменная . Значения , для трёх уравнений и предварительные выводы по необходимому условию идентифицируемости представлены в таблице.

Урав- нение	число эндогенных переменных в уравнении	число пред-определенных переменных в уравнении	Вид неравенства	Вид идентифицируемости уравнения
1	2	1		Сверхиденти-фицируемо
2	2	1		Сверхиденти-фицируемо
3	2	1		Сверхиденти-фицируемо
4	Уравнение - тождество

Замечание. Уравнение 4 представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.

Проверим для каждого из уравнений ещё и достаточное условие. Для этого составим матрицу коэффициентов при переменных модели.

1 уравнение	–1			0	0	0	0	0
2 уравнение	0	0	0	–1			0	0
3 уравнение	0		0	0	–1	0		0
Тождество	1	–1	0	1	0	0	0	1
	Матрица А

Матрица коэффициентов при переменных, не входящих в первое уравнение

	–1			0	0	, , где		0	0
	0	–1	0		0		0		0
	1	0	0	0	1		0	0	1

Ранг матрицы равен трём, так как определитель квадратной матрицы третьего порядка этой матрицы не равен нулю. Первое уравнение идентифицируемо.

Аналогично первому уравнению выписываем матрицу коэффициентов при переменных, не входящих во второе уравнение, и находим её ранг:

	–1			0	0	, где		0	0
	0		0		0		0		0	.
	1	–1	0	0	1		0	0	1

Второе уравнение также идентифицируемо.

Аналогично выписываем матрицу коэффициентов при переменных, не входящих в третье уравнение и находим её ранг:

	–1		0	0	0	, , где		0	0
	0	0	–1		0		0		0	.
	1	0	1	0	1		0	0	1

Третье уравнение также идентифицируемо.

Таким образом, все уравнения модели точно идентифицируемы. Для оценки их параметров применим двухшаговый метод наименьших квадратов.