4. Лабораторная работа № 3. Модель множественной регрессии. Проверка предпосылок 1-мнк. Оценка параметров обобщенной линейной эконометрической модели

4.1. Модель множественной регрессии (задание 3.1)

4.1.1. Теоретические замечания. На большинство экономических показателей влияет не один, а несколько факторных признаков. Поэтому для адекватного описания таких зависимостей необходимо использовать многофакторные эконометрические модели (табл. 4.1).

Таблица 4.1

Примеры многофакторных эконометрических моделей

Результативный признак	Факторные признаки	Спецификация модели	Данные для построения модели
Модели производственно-хозяйственной деятельности предприятий
Прибыль	- инвестиции, - стоимость основных производственных фондов, - фонд рабочего времени		данные по одному предприятию за месяцев (кварталов), данные по предприятиям концерна (отрасли)
Среднемесячная зарплата	- производительность труда, - коэффициент текучести рабочей силы, - фондоемкость
Объем продукции	- основной капитал, - рабочая сила	,	данные по одному предприятию за месяцев (кварталов, лет)
Индекс себестоимости продукции	- индекс производительности труда, - индекс фондоотдачи, - доля заработной платы в общих затратах		данные по одному предприятию за месяцев (кварталов), данные по предприятиям концерна (отрасли)

Продолжение 1 таблицы 4.1

Модели национальных экономик
Национальный доход	- фонд накопления, - заработная плата	,	данные по стране за месяцев (кварталов, лет)
Объем экспорта , за период	Объем экспорта , за период , - объем производства, - соотношение цен на внешнем и внутреннем рынках
Валовый внутренний продукт	- численность рабочих и служащих, занятых в сфере материального производства, - среднегодовой объем основных производственных фондов
Темпы экономического роста	- реальный среднедушевой ВВП, - бюджетный дефицит, - объем инвестиций, - внешний долг, - уровень инфляции
Социально-экономические модели
Расходы на питание	- общие расходы, - размер средней семьи		данные по семьям, средние показатели по регионам страны
Уровень оплаты жилищно-коммунальных услуг	- темп роста (уменьшения) реальной заработной платы, в % к соответствующему периоду предыдущего года, %; - уровень безработицы населения (по методологии МОП) в возрасте 15-70 лет, %; - среднемесячная заработная плата, грн.; - индексы потребительских цен;		данные по регионам страны
Уровень преступности	- уровень реальной заработной платы, - уровень безработицы

Продолжение 2 таблицы 4.1

Модели маркетинга (спроса и предложения)
Объем продаж предприятия	- цена предприятия, - цена конкурентов, - расходы на рекламу		данные по одному предприятию за месяцев (кварталов)
Цена квартиры	- число комнат, - район, - общая площадь квартиры, - жилая площадь, - тип дома, - наличие балкона		данные по городу по квартирам

Формулы для расчета оценок параметров многофакторных эконометрических моделей ( , - количество факторных признаков), а также показателей качества модели, прогноза, проверки статистических гипотез относительно параметров модели аналогичны формулам для однофакторных эконометрических моделей ( ), [3].

Воспользуемся матричной формой записи многофакторной модели:

, (4.1)

где:

, , , .

– матрица-вектор зависимой переменной; – матрица наблюдений независимых переменных размерностью (единичный столбец добавляется в эту матрицу для получения коэффициента в регрессионном уравнении). – матрица-столбец размерностью . – вектор-матрица случайных отклонений (возмущений) размерностью . Величины оцениваются на основе выборочных наблюдений, поэтому расчетные показатели не являются истинными, а представляют собой их статистические оценки.

Теоретическая модель (4.1) представляется как эмпирическая в матричной записи

. (4.2)

Оценка параметров модели множественной регрессии производится с помощью МНК по формуле:

. (4.3)

При этом:

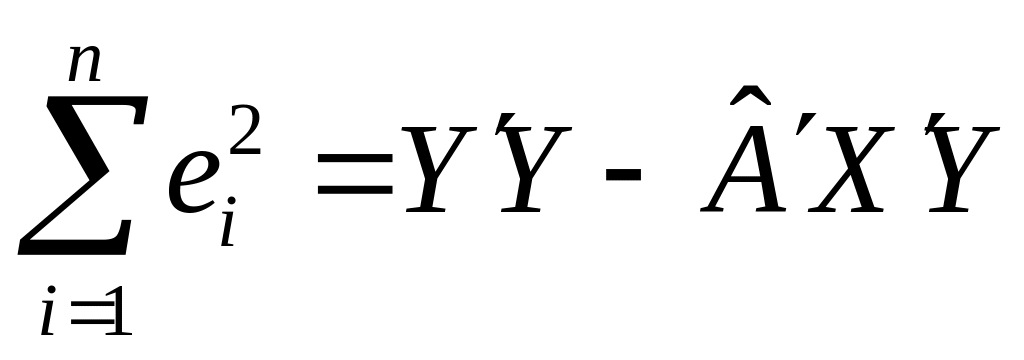. (4.4)

При построении модели множественной регрессии отбор наиболее существенных факторов, воздействующих на результативный признак, проводится на основе качественного, теоретического анализа в сочетании с использованием статистических приемов.

Сначала на основе содержательного анализа составляется перечень показателей . Затем производится сбор статистической информации и предварительный анализ данных, после чего осуществляется сравнительная оценка и отсев части факторов.

Для отбора показателей в регрессионную модель составляется матрица парных коэффициентов корреляции , измеряющая тесноту связи каждого из факторов с результативным признаком и между собой.

Корреляционная матрица имеет вид:

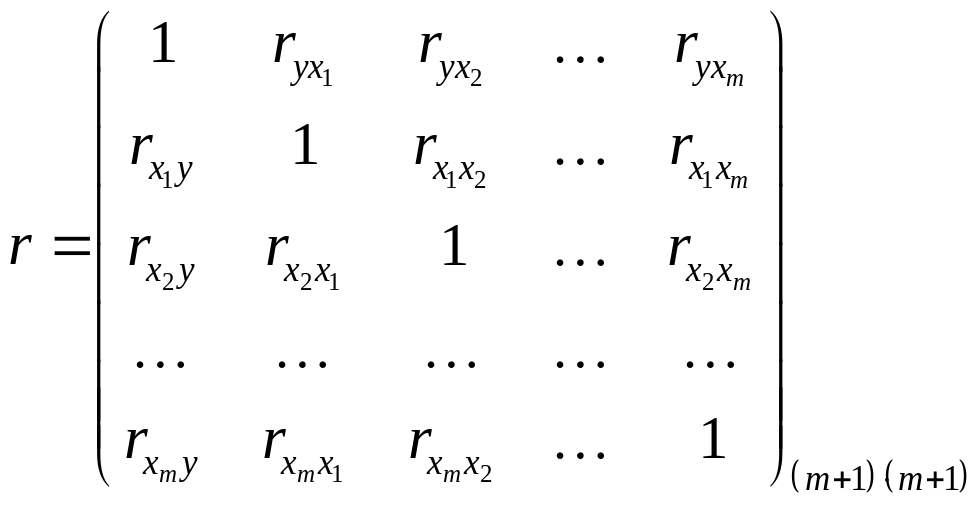. (4.5)

Путем анализа корреляционной матрицы производится отбор факторов для построения модели. Существуют две схемы отбора факторов для модели: метод включения – дополнительное введение фактора и метод исключения – исключения факторов из полного его набора.

Первая схема: признак включается в уравнение в том случае, если его включение существенно увеличивает значение множественного коэффициента корреляции, рассчитываемого по формуле

, (4.6)

где – определитель корреляционной матриц, а – алгебраическое дополнение элемента той же матрицы .

Примечание. Из практики можно считать, что существенным увеличением является увеличение множественного линейного коэффициента корреляции не менее, чем на 10%.

Так как значение множественного коэффициента корреляции зависит от количества включаемых в модель аргументов , то при расчетах необходимо использовать скорректированный множественный коэффициент корреляции:

. (4.7)

Этот коэффициент также необходимо проверить на значимость с помощью -критерия Фишера

. (4.8)

Значение - статистики рассчитанное по формуле (4.8) сравнивается с табличным . Если , то проверяемый множественный коэффициент корреляции значим.

Расчет по формуле (4.7) скорректированных множественных коэффициентов корреляции и их проверка по -критерию Фишера позволяет последовательно отбирать факторы, оказывающие существенное влияние на результативный признак. При этом первым в уравнение включается фактор, наиболее тесно коррелирующий с , вторым – тот фактор, который в паре с первым из отобранных дает максимальное значение и т.д.

На каждом шаге получают новое значение множественного коэффициента корреляции , бóльшее, чем на предыдущем. Тем самым определяется вклад каждого отобранного фактора в объясненную дисперсию .

Вторая схема пошаговой регрессии основана на последовательном исключении факторов с помощью -критерия Стьюдента. Она заключается в том, что после построения уравнения регрессии и оценки значимости всех коэффициентов регрессии из модели исключается тот фактор, коэффициент при котором незначим и имеет наименьшее значение -критерия. После этого получают новое уравнение множественной регрессии и снова производят оценку значимости всех оставшихся коэффициентов. Если среди них окажутся незначимые, то опять исключают фактор с наименьшим значением -критерия. Процесс исключения факторов останавливается на том шаге, когда все регрессионные коэффициенты становятся значимыми.

Расчётный -критерий Стьюдента определяют по формуле

, (4.9)

где:

, (4.10)

. (4.11)

Здесь – диагональный элемент матрицы .

Замечание. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов в 6-7 раз меньше объема совокупности, по которой строится регрессия.

После отбора факторов по одной из указанных схем и построения множественной регрессионной модели осуществляется статистическая проверка этой модели по методике, аналогичной рассмотренной для статистического анализа однофакторной регрессионной модели.

Проверку качества уравнения регрессии осуществляют с помощью коэффициента детерминации, множественной корреляции и средней относительной ошибки аппроксимации.

Коэффициент детерминации рассчитывается по формуле:

. (4.12)

Коэффициент множественной корреляции равен: .

Статистическая значимость коэффициента детерминации проверяется аналогично путём сравнения и , где

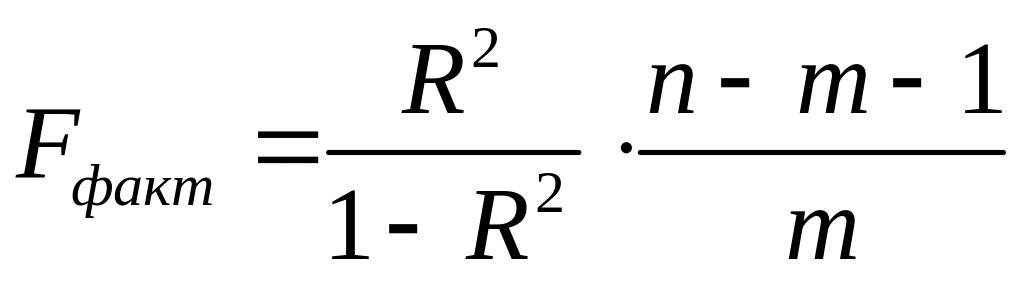. (4.13)

Табличное значение критерия Фишера зависит от уровня значимости и степеней свободы . Если , то принимается гипотеза о том, что статистически значим.

Для проверки значимости коэффициента множественной корреляции вычисляют -критерий Стьюдента:

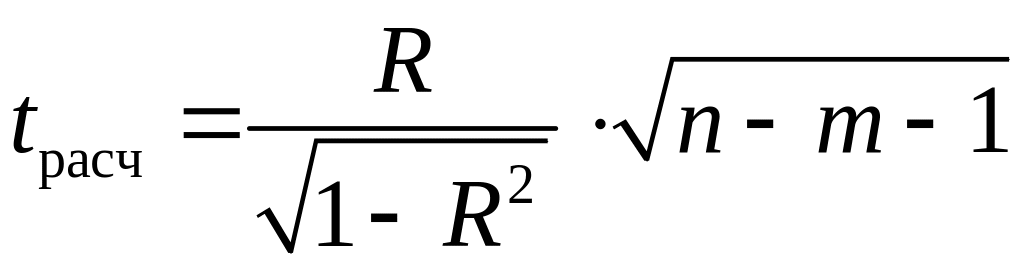. (4.14)

По таблице находим – соответствующее табличное значение t-критерия Стьюдента с степенями свободы, и уровнем значимости .

Если , то коэффициент множественной корреляции между регрессантом и регрессорами значим.

Для определения стандартных ошибок и нахождения доверительных интервалов оценок параметров используется дисперсионно-ковариационная матрица

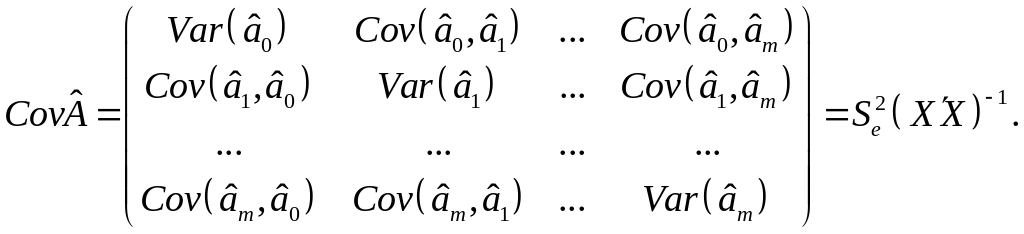(4.15)

Значимость коэффициентов уравнения регрессии проверяется с помощью сравнения фактических и табличных значений критерия Стьюдента:

, (4.16)

где , а – диагональный элемент матрицы .

Если , то коэффициент считается статистически значимым. Доверительные интервалы для параметров модели имеют вид

(4.17)

Средняя относительная ошибка аппроксимации находится по формуле

(4.18)

4.1.2. Организация данных и расчетов на листе MS Excel. Рассмотрим пример выполнения лабораторной работы № 3 (задание 3.1). Для выполнения задания 1 нужно создать новую рабочую книгу MS Excel, в ячейки которого ввести исходные данные задачи (рис. 4.1): значения показателей производительности труда - (млн. грн./год), фондоемкости (тыс. грн.), стаже работы (года), текучести кадров (в долях), средней заработной плате (тыс. грн.) и потерях рабочего времени (в долях).

Рис. 4.1. Исходные данные лабораторной работы № 3.

Для построения модели применим алгоритм пошаговой регрессии. На первом шаге построим пятифакторную линейную модель: . Для этого во вкладке «Сервис» выберем пункт «Анализ данных», в котором в свою очередь выберем функцию «Регрессия». После этого появится диалоговое окно, в котором нужно ввести ссылки на входные интервалы, выделяя их последовательно курсором. Следует отметить, что ссылка на значения факторов-аргументов должна быть неразрывной. Также нужно установить другие необходимые параметры задачи (например, «вывод остатков») и нажать «ОК». После этого появится отчет, такой как представлен на рис. 4.3.

Рис. 4.2. Диалоговое окно функции «Регрессия»

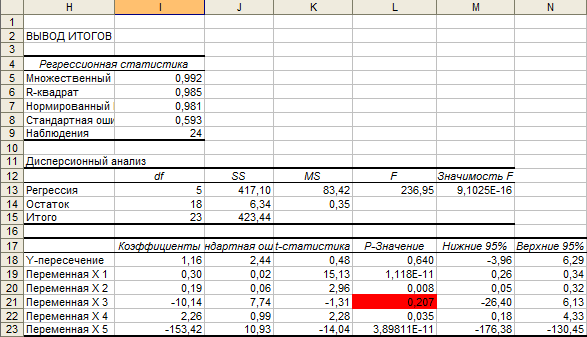
Рис. 4.3. Отчет функции «Регрессия» (шаг 1).

4.1.3. Построение модели множественной регрессии методом исключения (включения) факторов в модель. Из полученного отчета (рис. 4.3) выпишем уравнение регрессии ( ).

Значимость уравнения множественной регрессии в целом определяется с помощью статистического -критерия Фишера (4.8). В отчете функции «Регрессия» (раздел «Дисперсионный анализ») в ячейке хранится значение , которое можно использовать для проведения - теста. Можно использовать второй подход и проверить выполнение неравенства (где заданный уровень значимости). Для нашего примера (рис. 4.3, значение в ячейке ). Так как выполняется условие ( ), то пятифакторное уравнение регрессии значимо с надёжностью не менее 95%.

Проверку значимости коэффициентов полученного уравнения можно выполнить двумя способами. Первый - по критерию Стьюдента (формулы 2.9 – 2.12). Второй – проверить выполнение неравенства , (где заданный уровень значимости). Значения хранятся в столбце « -значение» отчета функции «Регрессия» (ячейки ). Заметим, что свободный член обычно не проверяется на статистическую значимость. В столбце « -значение» (рис. 4.3) только одно значение (ячейка ) для переменной больше заданного уровня значимости . Следовательно оценка коэффициента не значима, оценки остальных коэффициентов регрессии , , , статистически значимы с достоверностью 95%.

На втором шаге построим четырехфакторную линейную модель: . Из полученного отчета (рис. 4.4) выпишем уравнение регрессии ( ). Анализируя значения в столбце « -значение» отчета функции «Регрессия» (ячейки , рис. 4.4) делаем вывод, что все они удовлетворяют условию , . Следовательно все коэффициенты модели статистически значимы.

Используя данные отчета функции «Регрессия» (раздел «Вывод остатков») рассчитаем среднюю относительную ошибку аппроксимации четырехфакторной модели. Для этого в ячейки (рис. 4.5) скопируем значения результативного признака , в ячейки введем формулы как указано в табл. 4.2.

Рис. 4.4. Отчет функции «Регрессия» (шаг 2).

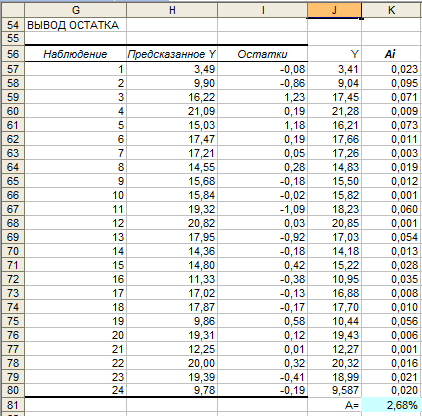
Рис. 4.5. Отчет «Вывод остатка» функции «Регрессия» (шаг 2) и расчет средней относительной ошибки аппроксимации модели.

Таблица 4.2.