1.4 Определение степени подвижности

Для выполнения анализа или проектирования механизма необходимо знать законы движения и положения всех звеньев, которые зависят от числа степеней свободы механизма, т. е. от числа обобщённых координат, определяющих законы движения и положения звеньев механизма. Числом степеней свободы механизма называется число независимых параметров (обобщенных координат), определяющих положение всех его звеньев относительно стойки. Основные структурные формулы были составлены для плоских механизмов Чебышёвым П.Л. (1821-1894) и Грюблером М. (1851-1935) , для пространственных – Сомовым П.И. (1852-1919) и Малышевым А.П. (1879-1962), в основу которых положены одинаковые принципы [5].

Русским учёным Чебышёвым П.Л. (1821-1894) были впервые выведены формулы, позволяющие определить число степеней свободы кинематической цепи или механизма в зависимости от числа звеньев и кинематических пар. Рассмотрим, механизм, состоящий из n подвижных звеньев, образующих кинематическую цепь. Пока звенья не соединены в кинематические пары, каждое из них имеет шесть степеней свободы (степеней подвижности). Механизм отличается от кинематической цепи тем, что у него одно неподвижное звено – стойка, которое потеряло все шесть степеней свободы. Следовательно, все звенья до соединения в кинематическую цепь имели 6n степеней подвижности. После сборки звеньев в кинематическую цепь мы получим кинематические пары различных классов (с разными степенями подвижности). Предположим, что наша кинематическая цепь имеет кинематические пары всех пяти классов. Примем следующие обозначения:

Р₁- количество одноподвижных кинематических пар V класса в образованной кинематической цепи,

Р₂ - количество 2-xподвижных кинематических пар IV класса,

Р₃- количество 3-xподвижных кинематических пар III класса,

Р₄- количество 4-xподвижных кинематических пар II класса,

Р₅ количество 5-типодвижных кинематических пар I класса.

Каждая кинематическая пара ограничивает перемещение звеньев, т.е. устраняет у них число степеней свободы, равное ее классу. Каждая кинематическая пара 5 класса отбирает у звеньев 5 степеней свободы. Все пары V класса отнимут у звеньев 5 Р₁ степеней свободы, IV класса - 4Р₂, III класса - 3Р₃, II класса - 2Р₄, I класса - 1Р₅. Если из общего количества степеней свободы звеньев 6n вычесть все потерянные степени свободы, получим число степеней подвижности кинематической цепи, обозначаемого символом W

(1.1)

Формула (1) носит название формулы Сомова - Малышева и впервые была получена Малышевым для пространственных механизмов.

Степенью подвижности механизма называется количество независимых координат, которые необходимо задать для определения положений звеньев механизма в системе координат, жестко связанной со стойкой.

Все звенья плоского механизма в движении на плоскости могут иметь три степени подвижности, а кинематические пары соответственно могут быть одно- или 2 –хподвижными (т.е. только V и IV классов). Общее количество степеней подвижности всех звеньев плоского механизма равно 3(n-1). Пары V класса теряют две степени подвижности, V - одну. Таким образом, степень подвижности плоского механизма может быть определена по формуле Чебышёва

. (1.2)

Для механизмов, представленных только поступательными парами V класса, например, клиновый механизм или механизм, представленный на рисунке 1.20, степень подвижности определяется по формуле Добровольского В.В. (1880-1957)

. (1.3)

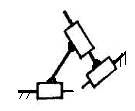
Рисунок 1.20 - Схема 2-хподвижного механизма с поступательными парами

О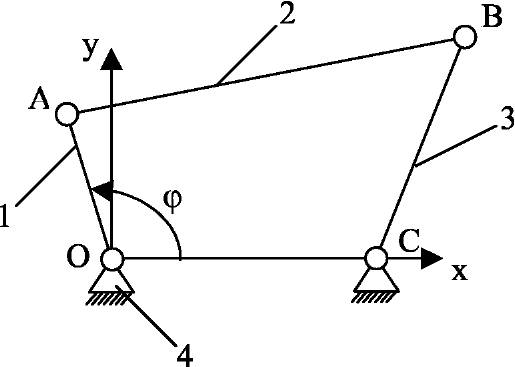 пределим степень подвижности шарнирного четырёхзвенника, изображенного на рисунке 1.21.

Рисунок 1.21 - Шарнирный четырёхзвенник

Звено 1 - кривошип- совершает вращательное движение вокруг оси О (полный оборот);

2 звено АВ- шатун- совершает плоско- параллельное движение;

3 звено ВС- коромысло (или балансир)- совершает возвратно- вращательное движение вокруг оси С (неполный оборот);

4 звено ОС- стойка (станина)- неподвижное звено.

Количество подвижных звеньев n. Кинематические пары: 4-1, 1-2, 2-3, 3-4. Имеем 4 одноподвижные пары V класса. Относительное движение всех звеньев плоское. Механизм плоский, следовательно для определения степени подвижности воспользуемся формулой (1.2) Чебышёва

Механизм имеет степень подвижности равную 1. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, жестко связанной со стойкой, чтобы определить положения всех остальных звеньев. В данном случае достаточно задаться углом поворота кривошипа .

Определим степень подвижности кулачкового механизма, изображенного на рисунке 1.22. Здесь звенья 1- кулачок, 2- толкатель, 3-ролик, 4- стойка. Количество подвижных звеньев n=3. Кинематические пары 1-4, 2-4, 2-3 V класса и 3-1 - высшая плоская кинематическая пара IV класса ( ). Определим W по формуле Чебышёва (1.2)

.

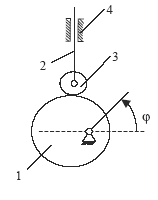
Рисунок 1.22 - Кулачковый механизм

Полученный результат объясняется наличием независимых между собой 2 координат - угла поворота кулачка и угла поворота ролика (относительного скольжения ролика).