8.2 Эвольвента и её свойства

Наиболее распространенным в технике является эвольвентное зацепление. Названо так потому, что боковые профили зубьев выполнены по эвольвенте. Эвольвентное зацепление предложено Эйлером (1707-1783) во второй половине XVIII века. Получило широкое распространение вследствие простоты изготовления эвольвентных зубьев [1]

.

Чтобы изучить свойства эвольвентного зацепления, расчет геометрических параметров и качественные его характеристики, надо знать – что такое эвольвента и каковы ее свойства.

Изобразим окружность, которую будем считать неподвижной (рисунок 8.4.) Проведем касательную к этой окружности. Точку касания обозначим А₀. Если обкатывать эту прямую по окружности без скольжения, то точка А₀ прямой линии опишет некоторую кривую. Эта кривая и есть эвольвента. Прямую можно обкатывать в двух направлениях. При этом будет образовано две ветви эвольвенты. Точка А₀ – начало эвольвенты – называется точкой заострения эвольвенты.

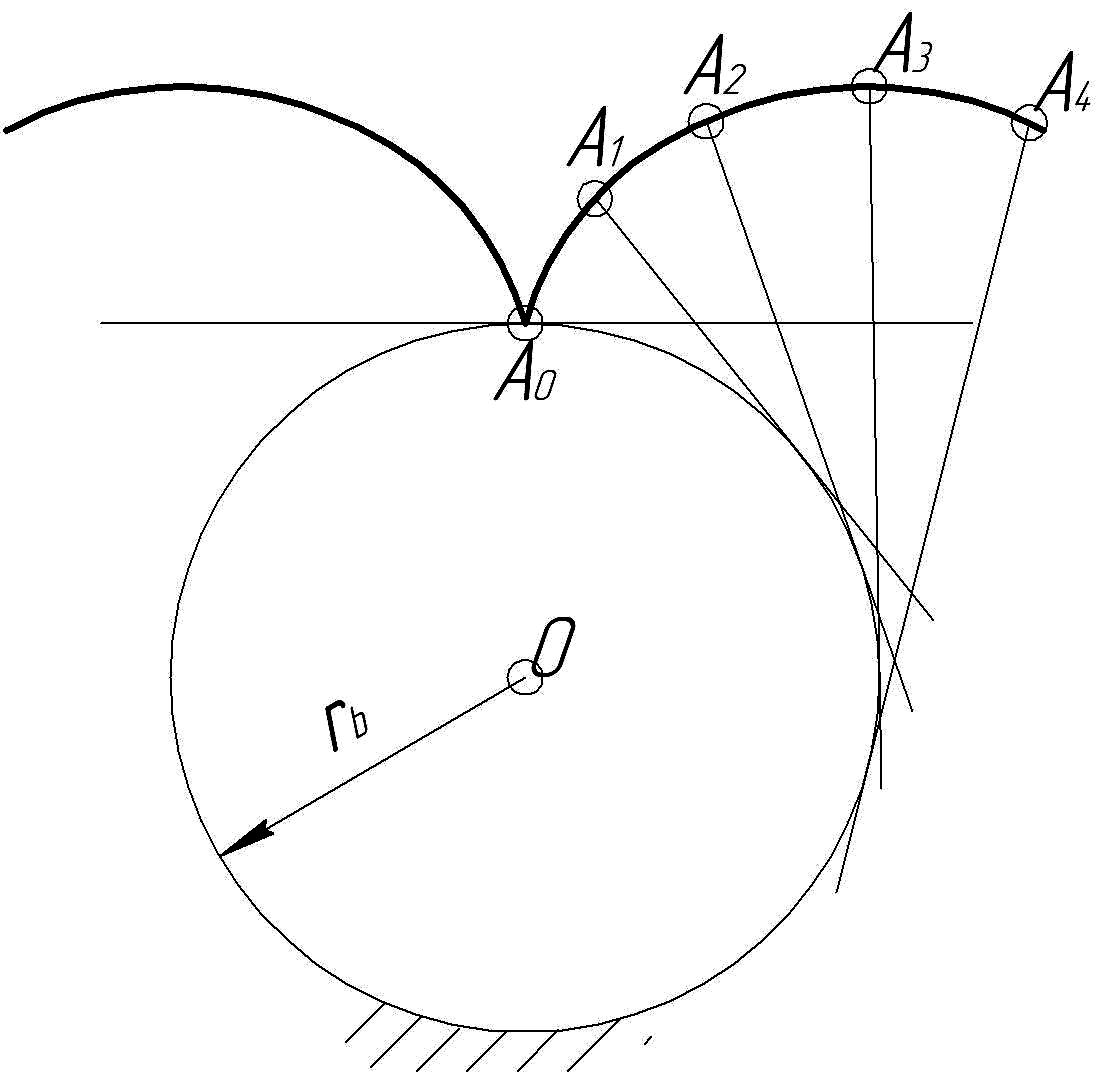
Рисунок 8.4 – Образование эвольвенты

Окружность, по которой катится прямая линия, точка которой образует эвольвенту, называется основной окружностью.

Стандартное обозначение радиуса основной окружности – r_b.

Прямая, обкатывающаяся без скольжения по основной окружности, называется производящей прямой.

Эвольвентой окружности называется плоская кривая, которую описывает любая точка прямой линии, катящейся по окружности без скольжения. Эвольвента – это спиралеобразная кривая, имеющая две ветви с точкой заострения на основной окружности.

Боковая поверхность зуба представляет собой эвольвентную поверхность, которую образует траектория прямой линии находящейся на плоскости, катящейся по основному цилиндру без скольжения. Образование эвольвентной поверхности может быть представлена следующим образом. На барабан (основной цилиндр) намотана лента. Если с неподвижного барабана сматывать ленту, то конец ленты (и любая прямая на ленте) будет описывать эвольвентную поверхность.

Основные свойства эвольвенты

1. Эвольвента не имеет точек внутри основной окружности. Прямая, образующая эвольвенту, катится по внешней стороне окружности и внутри ее не может быть точек эвольвенты. Точка А₀ - начало эвольвенты на основной окружности.

2. Форма эвольвенты полностью определяется радиусом основной окружности r_b и не зависит от других параметров. Если взять другую прямую или другую точку на прямой, то она опишет точно такую же эвольвенту. Все эвольвенты одной и то же основной окружности одинаковы.

3. Нормаль к эвольвенте в любой ее точке касательна к основной окружности. Проведем основную окружность радиуса r_b c центром в точке О (рисунок 8.5). Из точки А₀ построим эвольвенту. Через произвольную точку М на эвольвенте проведем касательную к основной окружности. Точку касания обозначим N. Так как образующая прямая катится по неподвижной окружности, то точка N является мгновенным центром скоростей а, следовательно, MN – мгновенный радиус для точки М. Скорость перпендикулярна MN – мгновенному радиусу вращения. Но в тоже время является касательной к траектории точки М – эвольвенте. MN  , а это значит, что касательная к основной окружности является нормалью к эвольвенте.

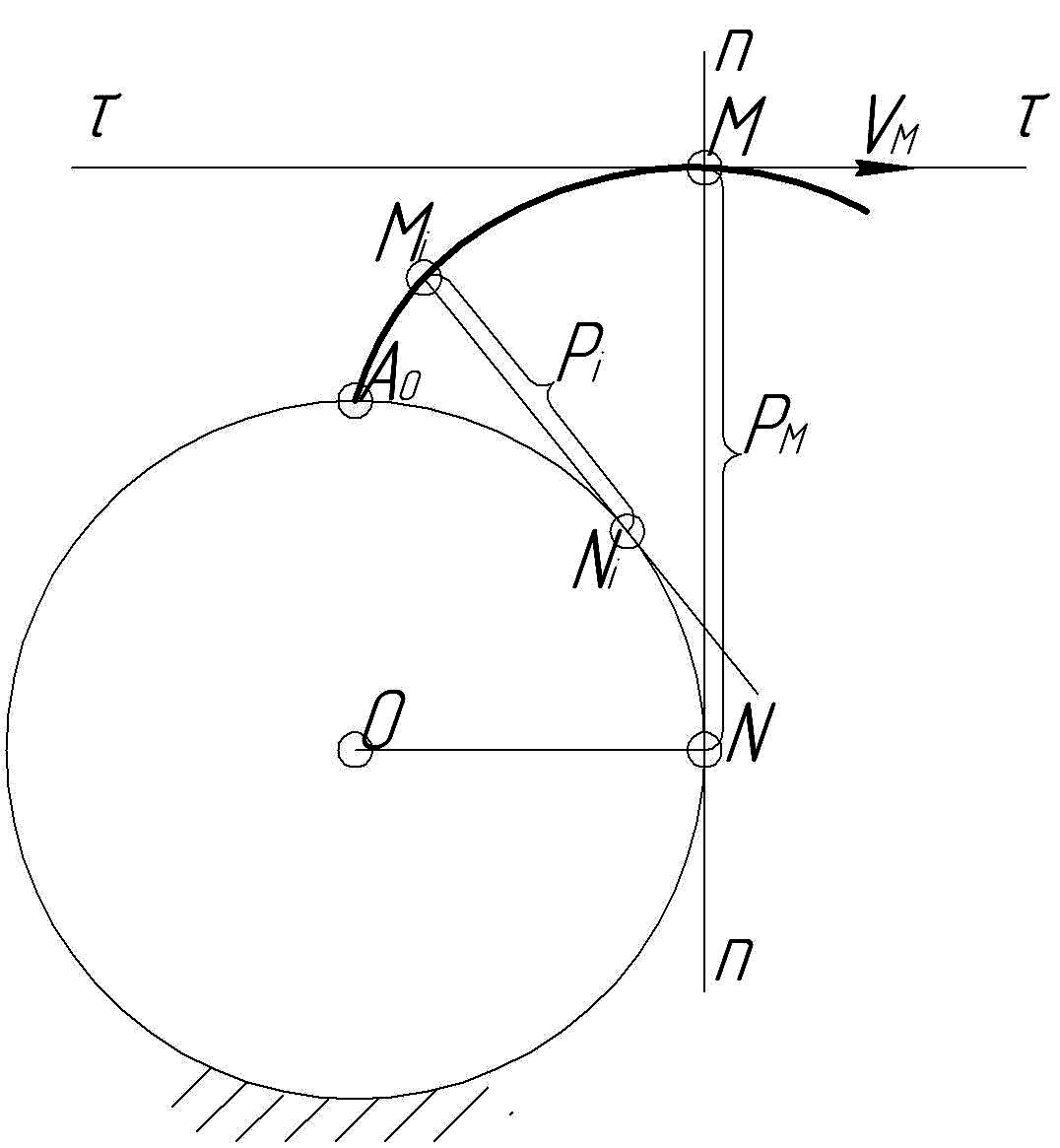
Рисунок 8.5 - Нормали к эвольвенте

4. Радиус кривизны эвольвенты в любой ее точке равен отрезку нормали от эвольвенты до основной окружности. Абсолютная линейная скорость точки М перпендикулярна радиусу кривизны траектории точки М. Следовательно MN=_M. В любой другой точке M_i радиус кривизны _i равен отрезку M_iN_i. В точке А₀ радиус кривизны эвольвенты равен нулю. Это точка заострения эвольвенты.

5. Расстояния по нормалям между двумя эвольвентами одной и той же основной окружности всюду одинаковы и равны расстоянию между началами этих эвольвент по дуге основной окружности. Изобразим две эвольвенты Э₁ и Э₂ одной и той же основной окружности, образованные двумя точками А и В одной и той же образующей прямой (рисунок 8.6) Если образующую обкатывать по основной окружности в направлении, обратном образованию эвольвенты, то в некоторый момент времени точки А₂ и В₂ совместятся с точками А₁ и В₁, а затем с точками А₀ и В_0. Следовательно:

А₂В₂ = А₁В₁ = А₀В₀ (8.6)

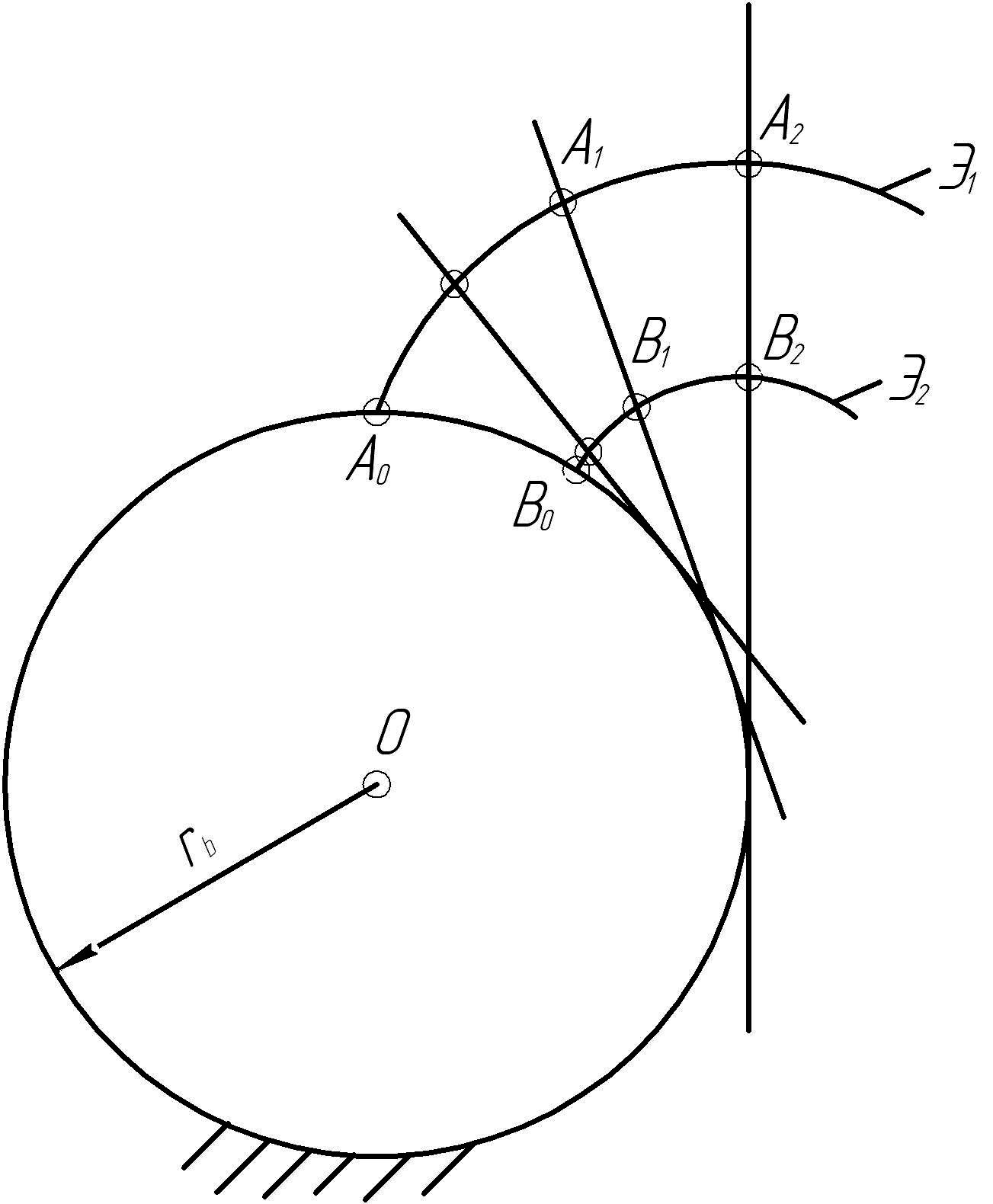
Рисунок 8.6 - Расстояния между эвольвентами по нормалям

6. Расстояние между двумя эвольвентами одного направления, измеренные по дугам концентрических окружностей, пропорциональны радиусам этих окружностей.

Изобразим основную окружность радиуса r_b и построим две эвольвенты одного направления Э₁ и Э₂ с началом их в точках А₀ и В₀ (рисунок 8.7). Проведем концентрическую окружность радиуса r₁ и точки ее пересечения с эвольвентами обозначим А₁ и В₁. Соединим все точки с центром окружности О. Повернем эвольвенту Э₂ до совмещения с эвольвентой Э₁.

Поскольку это одноименные эвольвенты, то при совмещении точек А₀ с В₀ должны совместиться точки А₁ и В₁. Следовательно, угол поворота В₀ОА- должен быть равен углу поворота В₁ОА₁ тоже - .

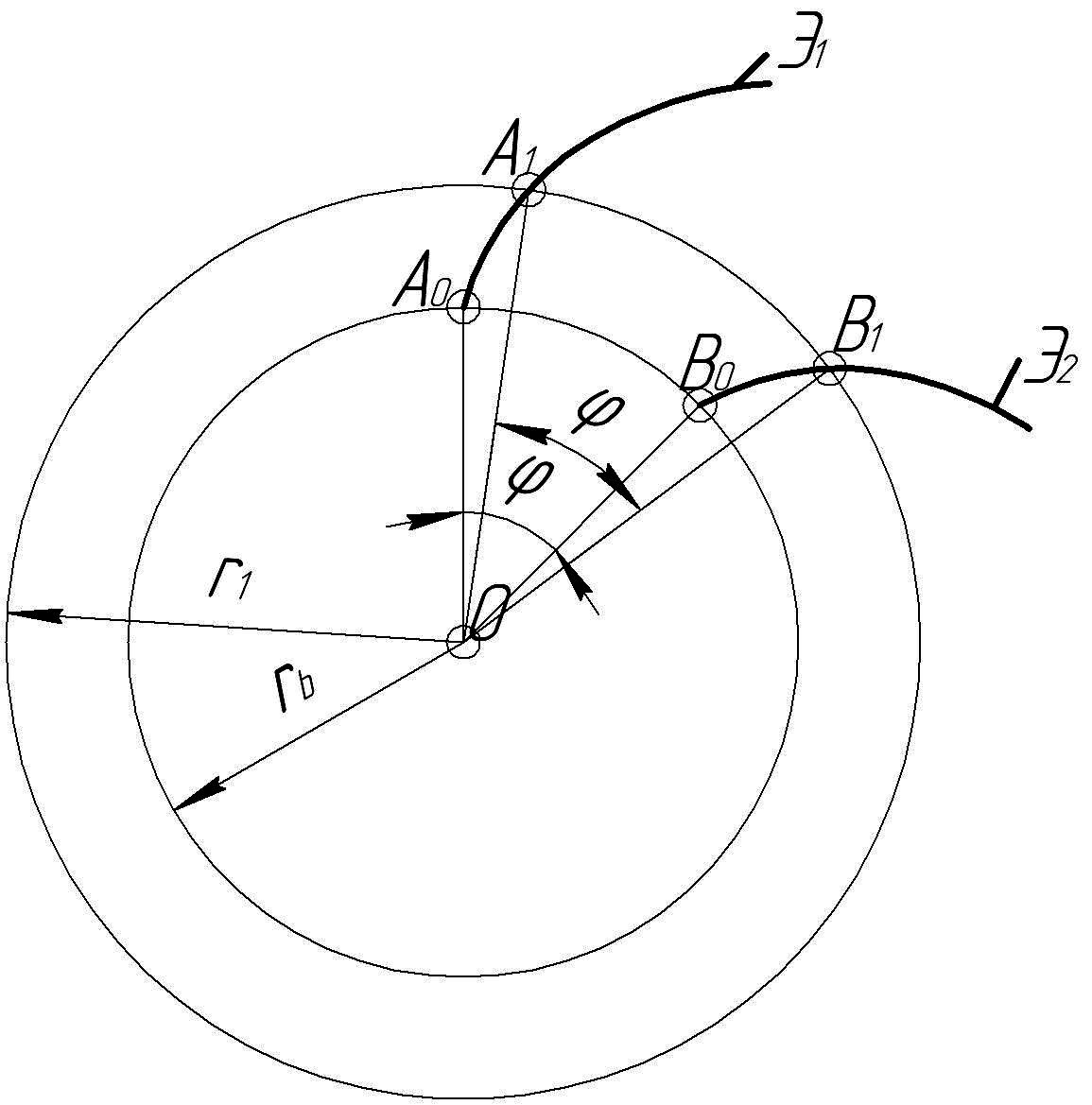
Рисунок 8.7 – Расстояния между эвольвентами по дугам концентрических окружностей

Определим длины дуг через их радиусы и углы поворота:

А₀В₀ = r_b;

А₁В₁ = r₁.

Разделим первое равенство на второе:

,

откуда получаем (8.7)

7. Угол давления эвольвенты в любой ее точке – это угол между направлением силы нормального давления и направлением абсолютной скорости данной точки.

Изобразим основную окружность радиуса r_b и построим эвольвенту с началом в точке А₀ (рисунок 8.8). Точку А₀ соединим с центром О основной окружности. На эвольвенте выберем некоторую произвольную точку А_. Передача движения при зацеплении эвольвент происходит за счет сил давления. Сила давления направлена по нормали к контактирующим профилям (касательной к основной окружности). Проведем нормаль n-n и изобразим вектор силы давления . Точку касания нормали к основной окружности В₀ соединим с О. Абсолютная скорость точки А_х , если колесо вращается вокруг центра О с угловой скоростью , направлена по касательной к траектории точки – окружности радиуса r_x(ОА₁). Соединим точку А_х с центром О и изобразим вектор скорости . Угол между направлением силы и скорости обозначим _х (угол давления).

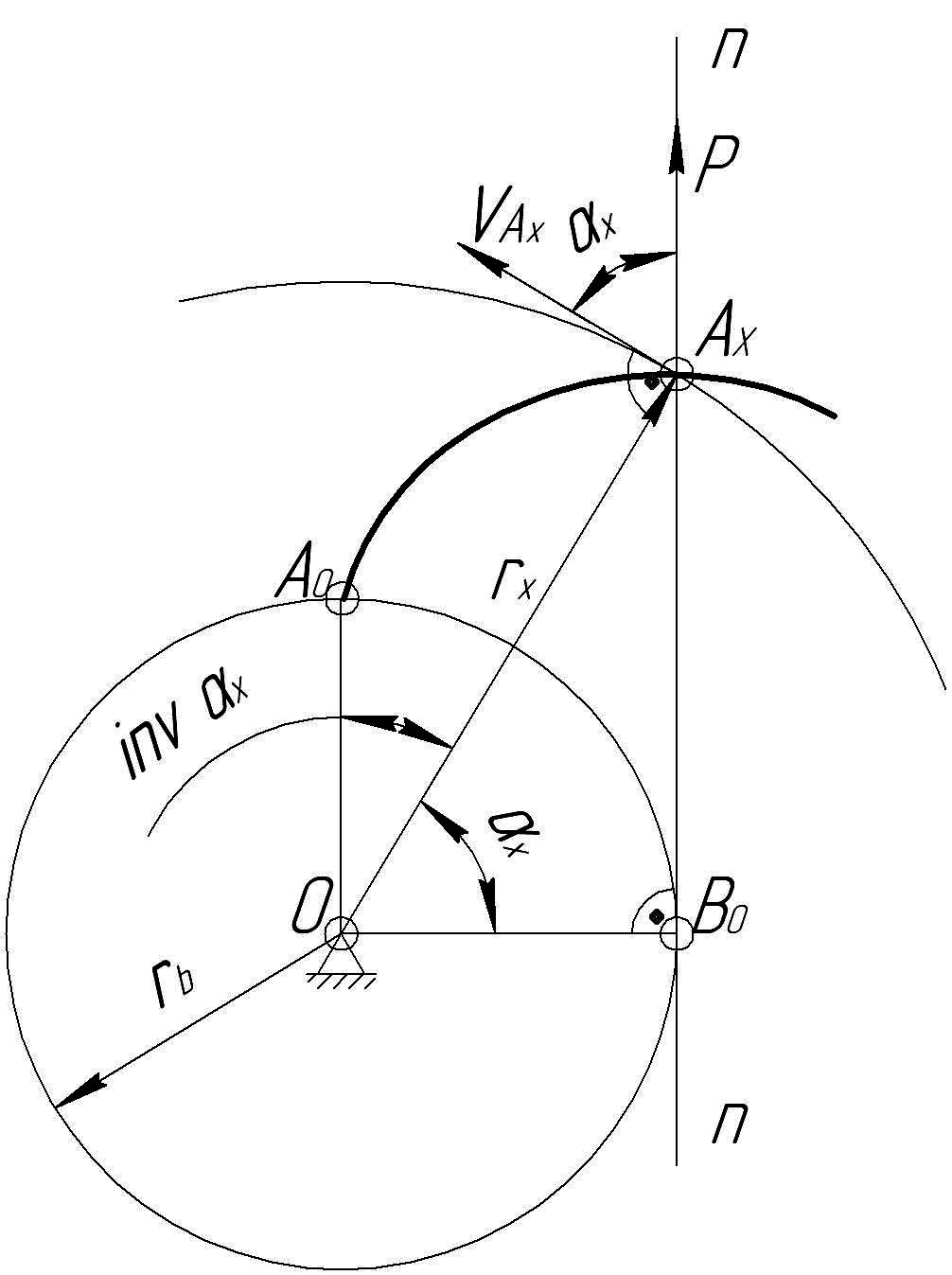
Рисунок 8.8 - Угол давления эвольвенты

Рассмотрим угол А_хОВ₀. Этот угол равен углу давления _х , так как стороны его перпендикулярны направлениям векторов силы и скорости: ОА_х  ; ОВ₀ . Таким образом, центральный угол между радиусом, проведенным в точку касания нормали к эвольвенте с основной окружностью, и радиусом, проведенным в данную точку эвольвенты, равен углу давления. В точке А₀ угол давления равен нулю.

Выведем уравнение эвольвенты в полярной системе координат. Для этого необходимо определить радиус – вектор любой точки эвольвенты и угловую координату этой точки от начала эвольвенты, т. е. от точки А₀.

Обозначим угол между радиусом, проведенным в начало эвольвенты А₀ и радиусом, проведенным в данную точку эвольвенты А_х – inv_х (инволюта _х). Установим зависимость между _х и inv_х. По свойству эвольвенты № 5:

А₀В₀ = А_хВ₀.

По рисунку 8.8 имеем:

А₀В₀ = (_х + inv_х) r_b , А_хВ₀ = ОВ₀ tg_x = r_btq_x ,

тогда получаем:

(_х + inv_x )  r_b = r_b  tg_x , откуда inv_x = tg_x - _x (8.8)

Это первое уравнение эвольвенты. Угол inv_x называется эвольвентной функцией, имеет радианную размерность и определяется по уравнению (8.8) в зависимости от угла _х , или по справочным таблицам, составленным по этому уравнению.

Из треугольника ОА_хВ₀ получаем второе уравнение эвольвенты:

(8.9)