2.3.2 Планы скоростей

Планом скоростей (ускорений) механизма называется фигура, на которой абсолютные скорости (полные ускорения) точек механизма изображаются векторами, начала которых находятся в произвольно выбираемом полюсе плана скоростей (ускорений).

Для удобства пользования планом скоростей (ускоений) концы векторов скоростей (полных ускорений) точек будем обозначать малыми буквами, соответствующими названиям точек на плане механизма (они называются изображениями точек на плане скоростей (ускорений)).

План скоростей (ускорений) считаем построенным, когда изображены векторы скоростей (ускорений) двух несовпадающих точек каждого непоступательного движущегося звена и одной точки каждого поступательно движущегося.

Несовпадающими называются такие точки, проекции которых на плоскость плана скоростей (ускорений) не совпадают.

Для сокращения количества точек, исследуемых при построении планов скоростей (ускорений), полезно учитывать следующие соображения.

Если два звена образуют плоскую цилиндрическую (вращательную) кинематическую пару, то принадлежащие им точки, лежащие на оси цилиндра, имеют одинаковые скорости (ускорения).

Если два звена образуют поступательную кинематическую пару, то две точки, принадлежащие звеньям и совпадающие в рассматриваемый момент времени, в общем случае имеют различные скорости и различные ускорения.

Часто при построении планов скоростей (ускорений) некоторые звенья считают материальными точками, так как их размеры малы по сравнению с размерами других звеньев (например, кулисные камни).

Методику построения плана скоростей (ускорений) рассмотрим на примере шарнирного четырехзвенника. Считаем заданными план механизма в исследуемом положении, закон движения кривошипа 1 – ω_1, ε₁ (см. рис. 2.2).

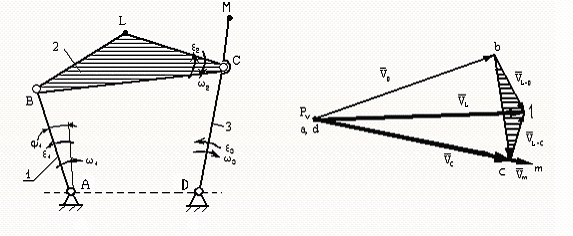
Рисунок 2.2 – План механизма Рисунок 2.3 – План скоростей

Обозначим прописными буквами латинского алфавита те точки, скорости (ускорения) которых будем определять.

Очевидно, рационально принять к рассмотрению точки А, В, С, D.

Начинать построение плана скоростей (ускорений)следует с рассмотрения точек того звена, закон движения которого известен (в нашем примере – это точки А и В кривошипа 1).

Точка А неподвижна, т.к. лежит на оси вращения кривошипа,

Модуль скорости точки В определяется известной формулой:

(2.7)

Вектор скорости точки В направлен по касательной к траектории этой точки (окружности радиуса АВ), т.е. перпендикулярно радиусу кривизны траектории ( АВ) в сторону, определяемую направлением вращения кривошипа 1. Теперь, зная модуль и направление скорости точки В, изобразим ее вектором P_Vb (см. рис.2.3). Для построения плана скоростей выберем масштабный коэффициент скорости μ_V , после чего длина вектора P_Vb может быть вычислена:

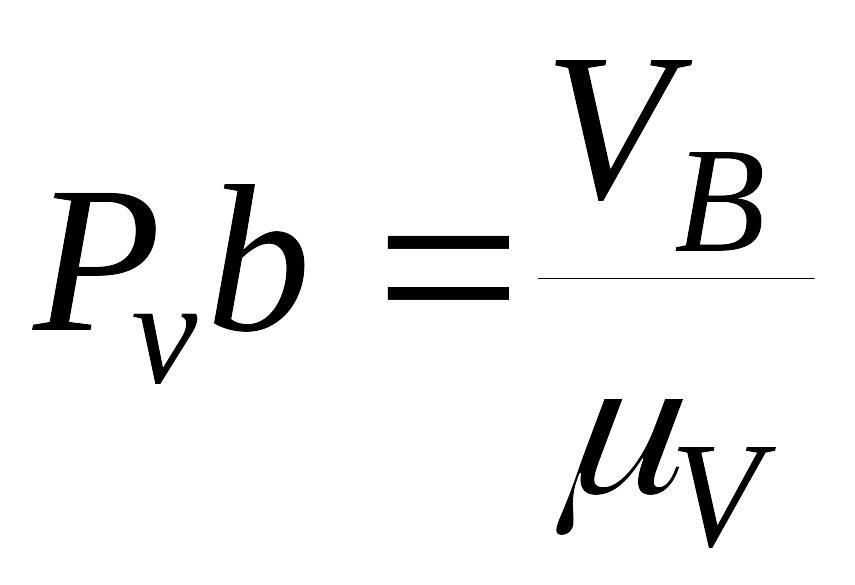(2.8)

Аналогично вычисляется длина вектора P_vа:

(2.9)

Т.е. изображение точки А (а) совпадает с полюсом плана скоростей P_V.

Следующей будет исследована точка С, для чего ее скорость свяжем векторным уравнением со скоростью точки В. Связь между скоростями (ускорениями) двух точек одного и того же звена проста и удобна в пользовании, когда это звено совершает поступательное или вращательное движение. В нашем же случае шатун 2, которому принадлежат точки В и С, совершает плоскопараллельное движение. Для выяснения связи между скоростями точек В и С разложим движение шатуна 2.

При разложении плоскопараллельного движения звена (в нашем случае – шатуна 2) на переносное - поступательное вместе с некоторой точкой - и относительное – вращательное вокруг оси, проходящей через эту точку, в качестве этой точки избирают такую, скорость (ускорение) которой известна (в нашем примере – это точка В), и которая расположена ближе к исследуемой точке (точке С).

В результате поступательного движения переносящей среды вместе с точкой В у скорости точки С появляется составляющая, равная скорости точки В:

(2.10)

В результате вращательного относительного движения шатуна 2 вокруг оси, проходящей через точку В, у скорости точки С появляется еще одна составляющая – скорость точки С относительно точки В - V_С-В, которая направлена перпендикулярно ВС.

(2.11)

В соответствии с теоремой о сложении скоростей, абсолютная скорость точки складывается из переносной и относительной, в нашем случае:

(2.12)

Для удобства анализа и решения векторных уравнений будем подчеркивать вектор одной чертой, если известен только его модуль или только положение его линии действия, и двумя чертами, если известны и модуль его, и положение линии действия.

С учетом уравнений (2.10) и (2.11) уравнение (2.12) принимает следующий вид:

(2.13)

Решаем уравнение графическим способом. Через точку b – конец первого слагаемого вектора на плане скоростей (рис. 2.3) проводим прямую перпендикулярно отркзку ВС, т.е. производим сложение векторов по правилу треугольника. Из точки P_V проводим прямую перпендикулярную отрезку СD до пересечения с предыдущей прямой в точке с.

Таким образом, построены векторы P_Vс и bc, изображающие скорости

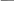V_С и V_C-B, модули которых могут быть легко вычислены пользуясь (2.8) :

Точка D неподвижна,

т.е. изображение точки D на плане скоростей (d) находится в полюсе плана скоростей P_V.

Таким образом, определены скорости двух несовпадающих точек каждого непоступательного движущегося звена, следовательно, построение плана скоростей закончено. Это значит, что возможно определение скорости любой точки, принадлежащей любому звену механизма, например, точки L шатуна.

Воспользуемся разложением плоскопараллельного движения отрезка BL на поступательное переносное движение вместе с точкой В и вращательное относительное вокруг оси,проходящей через точку В перпендикулярно плоскости чертежа, аналогично тому, как ранее было разложено движение отрезка ВС. Это позволит получить векторное уравнение связи скорости точки L со скоростью точки В:

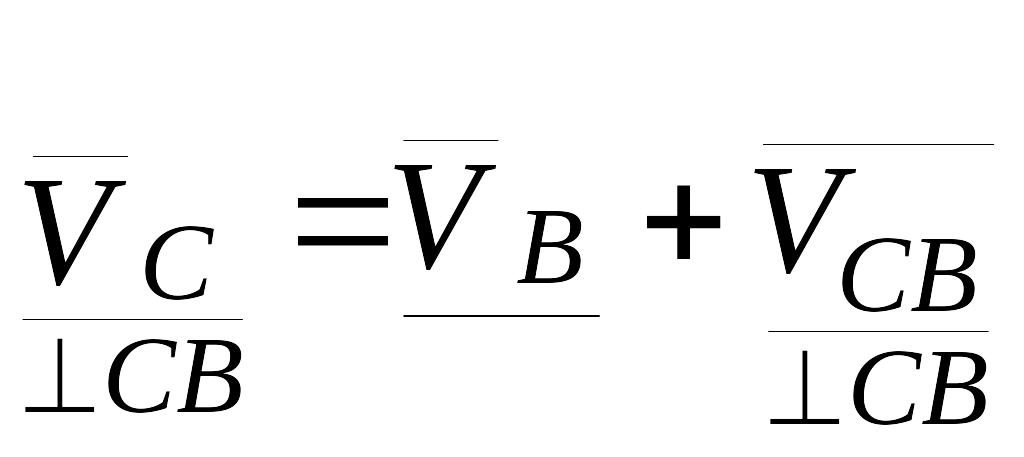(2.14)

Это уравнение содержат три скалярные неизвестные величины, следовательно, оно неразрешимо.

Свяжем скорость точки L со скоростью точки С, произведя разложение плоскопараллельного движения отрезка LC на переносное поступательное вместе с точкой С и относительное вращательное вокруг оси, проходящей через точку С:

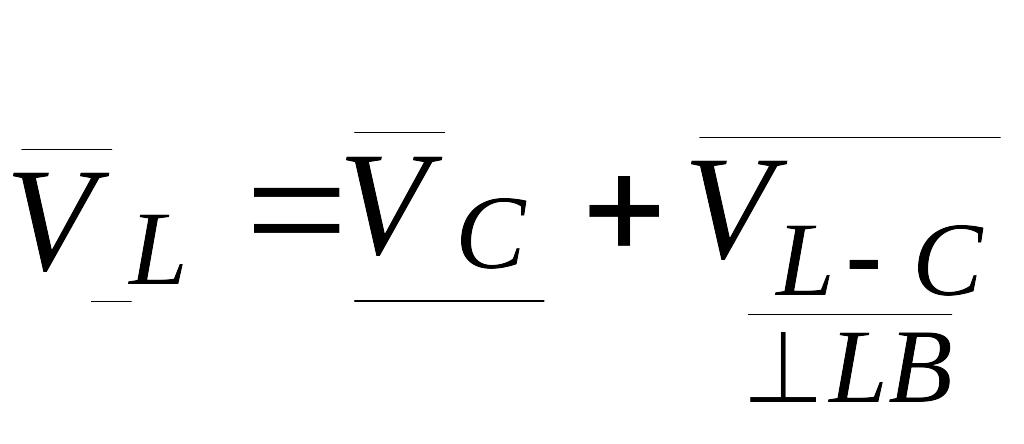(2.15)

Это уравнение тоже содержит три скалярные неизвестные величины, следовательно, оно неразрешимо.

Система векторных уравнений (2.14) и (2.15) содержит 4 скалярных неизвестных, следовательно, она разрешима. Решение получено графическим методом (см. рис. 2.3). Вектор P_Vl изображает скорость точки L.

Полученный на плане скоростей треугольник blc подобен треугольнику BLC плана механизма, т.к. их стороны взаимно перпендикулярны (это следует из векторных уравнений, использованных для построения плана скоростей). Следовательно, их можно сделать равными, увеличив или уменьшив все стороны одного из них в одно и то же количество раз. Затем, если они сходственно расположены, их можно совместить, перемещая один из них в плоскости чертежа. В результате этого плоскопараллельного перемещения совпадут вершины этих треугольников: B и b, C и c, L и l. Очевидно, что наличие сходственности расположения треугольников можно проверить также на слух: если прочесть обозначения вершин обоих треугольников начиная с одного и того же звука и в одном и том же направлении (по ходу часовой стрелки), то звуки будут чередоваться в одной и той же последовательности, например, BLC и blc (а не BLC и bcl).

Отмеченные подобие и сходственность расположения фигуры на плане скоростей (blc) по отношению к фигуре на плане механизма (BLC) имеют место только в случае, когда фигура на плане механизма является неизменяемой (т.е. звеном). Изменяемых же фигур на плане механизма эта закономерность не касается. Чтобы убедиться в этом, достаточно сравнить фигуру abcd (треугольник) на плане скоростей с изменяемой фигурой ABCD (четырехугольником) на плане механизма.

Точка L является точкой общего положения и принадлежит звену, которое движется самым общим образом – плоскопараллельно. Поэтому решение конкретной задачи об определении скорости точки L можно считать доказательством теоремы подобия: неизменяемой фигуре на плане механизма соответствует подобная и сходственно расположенная фигура на плане скоростей (и ускорений).

Воспользуемся этой теоремой для отыскания скорости точки М: построим на плане скоростей фигуру dcm, подобную и сходственно расположенную по отношению к неизменяемой фигуре DCM, для чего воспользуемся пропорцией.

.

Из этой пропорции найдем длину отрезка dm и отложим его на плане скоростей.

.

Теперь абсолютную скорость точки М можно определить известным образом:

.

Выполнение договоренности об обозначении концов векторов скоростей (и полных ускорений) точек строчными буквами, соответствующими прописным буквам, обозначающим эти точки на плане механизма, приводит к следущей закономерности, удобной при пользовании планом скоростей (ускорений): конец вектора скорости (полного ускорения) любой точки плана механизма совпадает с изображением этой точки на плане скоростей (ускорений), а начало этого вектора совпадает с изображением той точки, относительно которой определяется скорость (полное ускорение).

Н апример, вектор скорости точки L отностельно точки В – V_L-B начинается в b и заканчивается в l. Вектор скорости точки В относительно точки L – V_В-L начинается в l и заканчивается в b. Вектор скорости точки L относительно точки А (вектор абсолютной скорости точки L) – V_L-А V _L начинается в а (т.е. P_V) и заканчивается в l. Вектор скорости точки А относительно точки L – V_А-L начинается в l и заканчивается в а. Это следует из векторных уравнений, использованных для построения плана скоростей.

Из приведенных примеров можно заключить, что стрелки на плане скоростей (ускорений) отражают направления лишь тех векторов, которые упомянуты в уравнениях, использованных для построения этих планов, а по окончании построения – не необходимы.

В свете изложенного очевидно, что если на плане скоростей некоторого механизма имеются изображения точек Q и M (т.е. q и m), то вектор qm изображает скорость точки М относительно точки Q – V_{М – Q, ,} вектор P_Vq изображает абсолютную скорость точки Q – V_Q,, вектор P_V m изображает абсолютную скорость точки М - V_М .

Следовательно,

Не имеет значения, принадлежат ли точки М и Q одному и тому же звену или разным и какие из них подвижны, а какие неподвижны.