2.3.7 Построение планов скоростей и ускорений кулисного механизма

Кулисные механизмы получили широкое распространение в машиностроительной и особенно в станкостроительной промышленности (привод резцовой головки строгального или долбежного станка, привод загребающей лапы погрузочной машины и т.д.).

Кулиса – это подвижное звено, которое служит направляющей для ползуна, часто называемого кулисным камнем. Кулиса может совершать различные движения: возвратно-вращательное, поступательное, вращательное.

Рассмотрим порядок и правила построения планов линейных скоростей и ускорений такого механизма и определим угловые скорости и ускорения его звеньев. В качестве примера возьмем плоский кулисный механизм - шестизвенник (рис. 2.6). Обозначим звенья и точки механизма, подлежащие исследованию. В нашем механизме : 1 – кривошип, 2 – камень, 3 – кулиса, 4 – камень, 5 – ползун, 6 – стойка. Заданы: план механизма, кинематические длины всех звеньев, закон движения (ω₁ = const) и исходное положение входного звена – кривошипа 1.

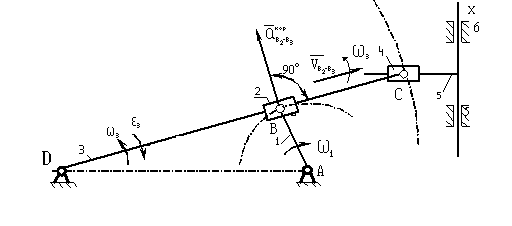
Рисунок 2.6 – План кулисного механизма

О пределяем скорость точки В₁ принадлежащей звену 1,V_B1. Условимся обозначать точку буквой с индексом, обозначающим то звено, которому точка принадлежит. Звено 1 совершает плоское вращательное движение. Вектор скорости точки B₁ направлен перпендикулярно радиусу вращения АB,

По модулю абсолютная скорость точки B₁

.

Из произвольно выбранной точки P_V, полюса плана скоростей, проводим луч перпендикулярно АB и откладываем отрезок P_V b₁ (рис. 2.7), длина которого определяется известным образом:

Определяем масштабный коэффициент плана скоростей:

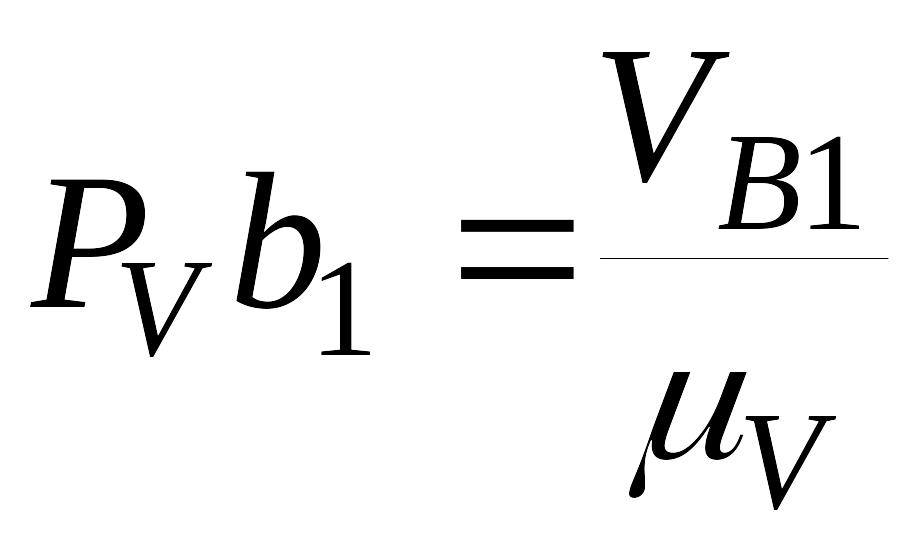
Рисунок 2.7 – План скоростей кулисного механизма

Определяем скорость точки B₂, принадлежащей звену 2 – кулисному камню. Звено 2 совершает плоскопараллельное движение. Точка B₂ – лежит на геометрической оси вращательной пары 1-2. Следовательно, абсолютные скорости точки B₁, принадлежащей звену 1, и точки B₂, принадлежащей звену 2, равны по модулю и совпадают по направлению . На плане скоростей они будут изображаться одним и тем же вектором P_Vb_1,2.

Определяем скорость точки B₃, принадлежащей звену 3 – кулисе. Вектор абсолютной скорости точки B₃ - V_B3 будет направлен по касательной к траектории точки B₃, совпадающей в настоящий момент времени с точками B₁ и B₂. Звено 3 совершает возвратно-вращательное движение вокруг центра D. Траектория точки B₃ – дуга о кружности с центром в точке D радиусa DB. Вектор абсолютной скорости V_B3 направлен по касательной к траектории точки B₃, а следовательно, по линии, перпендикулярной к DB.

Для определения V_B3 воспользуемся разложением сложного плоскопараллельного движения звена 2. Разложим это движение на переносное и относительное. Переносящая среда для звена 2 – звено 3, которое переносит камень в своем возвратно-вращательном движении. Переносное движение камня 2 – движение вращения вместе со звеном 3. Звено 2 в процессе сложного движения перемещается по звену 3, как по направляющей. Это является относительным движением звена 2.

Рассмотрим абсолютное движение точки B_2. Переносной скоростью точки B₂ является абсолютная скорость точки B₃, принадлежащей кулисе, как переносящей среде:

.

Второе движение – относительное, является поступательным движением звена 2 по звену 3. Относительная скорость точки B₂ по отношению к точке B₃ направлена вдоль отрезка BD:

.

Составляем векторное уравнение скорости движения точки B₂:

;

DB || DB

В полученном векторном уравнении две неизвестных скалярных величины: модули скоростей V_B3 и V_{B2 – B3}. Решаем уравнение графическим методом. Из полюса плана скоростей P_V проводим линию, перпендикулярную BD, так как абсолютная скорость точки B₃ будет изображаться отрезком, выходящим из P_V. Через точку b_1,2 плана скоростей проводим линию параллельно BD– линию действия вектора скорости V_{B2 – B3} .Точку пересечения проведенных прямых обозначаем b₃. По правилу сложения векторов направляем стрелки на изображении векторов соответствующих скоростей. P_Vb₃ - изображение скорости V_B3, b₃b_1,2 – изображение скорости V_{B2 – B3}. Модули скоростей:

;

.

Определяем скорость точки С. Точка С является геометрической осью шарнира и принадлежит одновременно звену 3 – кулисе и звену 4 – камню.

Траектория точки С – окружность радиуса CD.Вектор абсолютной скорости точки С направлен перпендикулярно радиусу CD.

Рассмотрим точку С, как принадлежащую звену 3. Воспользовавшись теоремой подобия, можем составить пропорцию:

.

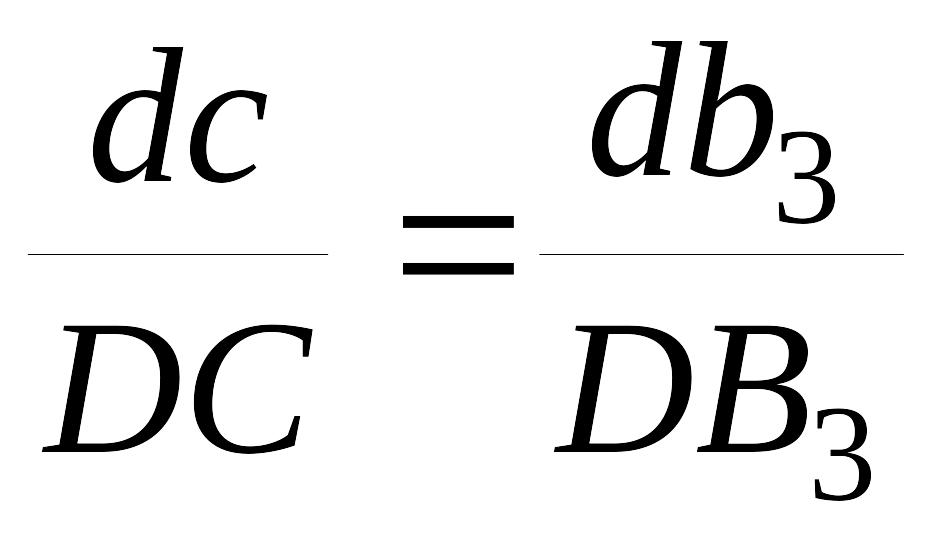Определяем длину отрезка, изображающего на плане скоростей:

.

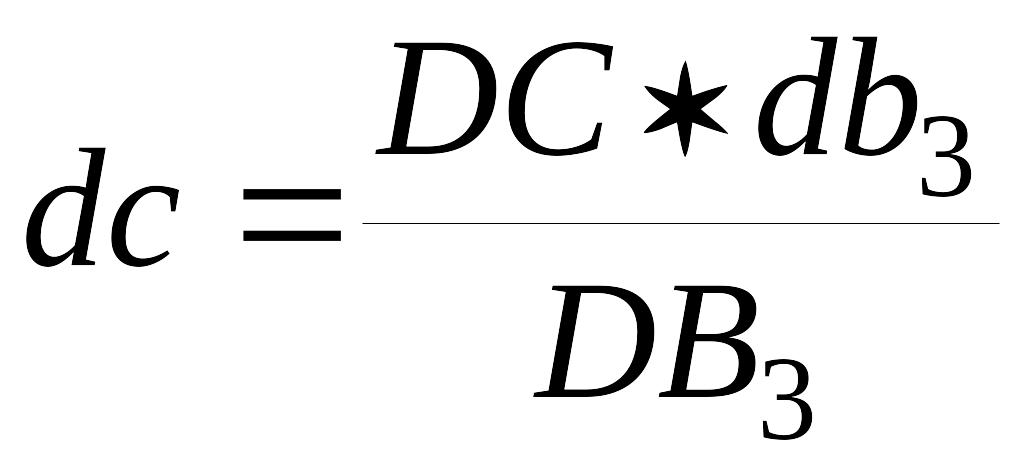На продолжении отрезка db₃ откладываем отрезок dc и обозначаем конец вектора c.

Определяем модуль скорости точки C:

Определим скорость точки C₅ принадлежащей звену 5 – ползуну. Для этого воспользуемся разложением движения звена 4 на переносное и относительное. За переносное примем движение камня 4 вместе с ползуном 5 вдоль оси х – х – поступательное прямолинейное движение. За относительное примем перемещение звена 4 вдоль звена 5 перпендикулярно оси х – х. Абсолютная скорость любой точки звена 5, совершающего поступательное прямолинейное движение, направлена вдоль оси х – х.

.

Относительная скорость точки C₄ V_{C4 – C5}, по отношению к точке C₅, расположенной на звене 5 и совпадающей в данный момент времени с точками C₃ и C₄ при поступательном движении звена 4 вдоль звена 5, направлена перпендикулярно оси х – х:

Составляем векторное уравнение для определения абсолютной скорости точки C4:

V_C4 =V_C5 + V_{С4 - C5} .

|| x – x x - x

В этом уравнении две неизвестных скалярных величины: модули скоростей | _C5| и | _{С4 - C5}|. Решаем уравнение графическим методом. Из полюса плана скоростей проводим прямую, параллельную оси х – х - линию действия вектора абсолютной скорости точки C₅ звена 5. Через точку c_3,4 на плане скоростей проводим прямую, перпендикулярную оси х – х, линию действия вектора относительной скорости . Точку пересечения этих прямых обозначим c₅. В соответствии с правилом сложения векторов направляем стрелки. Отрезок P_Vc₅ на плане скоростей – изображение абсолютной скорости точки C₅ звена 5 - _C5. Отрезок c₅ c_3,4 – изображение относительной скорости _{С4 - C5}.

Определяем модули скоростей:

;

.

Построение планов скоростей закончено.

Определяем угловые скорости звеньев.

Угловая скорость кривошипа (звена 1) нам задана – ω₁.

Угловая скорость звена 2 (кулисного камня), совершающего сложное плоскопараллельное движение может быть получена как векторная сумма угловых скоростей звена в переносном и относительном движениях:

.

В нашем случае переносная угловая скорость звена 2 это абсолютная угловая скорость звена 3 – переносящей среды:

.

Относительное движение звена 2 - это его поступательное движение вдоль

звена 3.

Таким образом мы получим, что угловая скорость звена 2 по модулю и направлению равна угловой скорости звена 3:

.

Определяем угловую скорость звена 3 – кулисы.

Модуль угловой скорости кулисы:

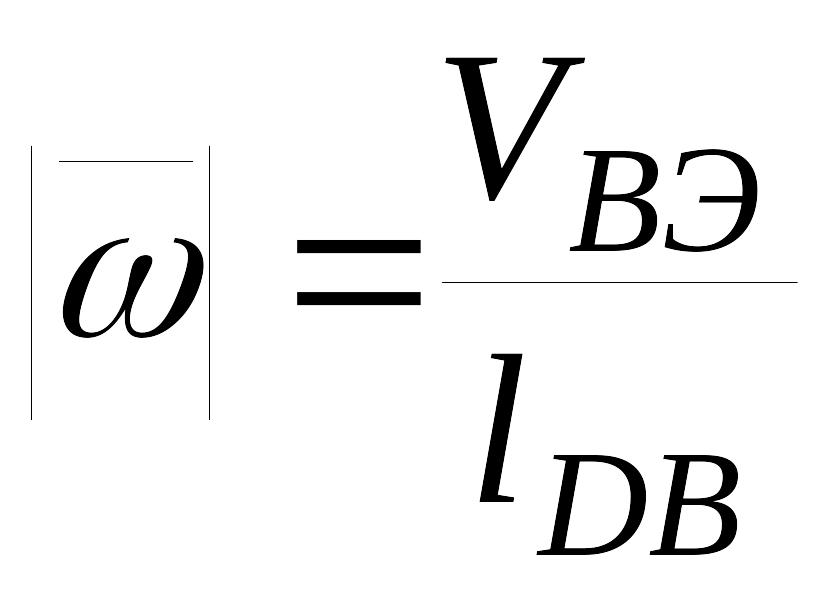
Звено 3 вращается против часовой стрелки (см. направление действия вектора V_B3).

Звено 4 (камень) в переносном и относительном движениях совершает поступательные движения. Поэтому его угловая скорость равна нулю:

.

З вено 5 (ползун) совершает поступательное движение: ω₅ = 0.

При построении планов ускорений кулисного механизма будем использовать обозначения соответствующих точек и разложение движения звеньев, принятые при построении планов скоростей.

Определяем ускорение точки B₁, принадлежащей вращающемуся звену 1. Ускорение точки B₁ равно векторной сумме нормального и тангенциального ускорений:

BА АB

Модуль нормального ускорения:

.

Вектор нормального ускорения всегда направлен к центру кривизны траектории точки. В нашем случае направлен от В к А (BА).

Модуль тангенциального ускорения:

Вектор тангенциального ускорения направлен по касательной к траектории точки (перпендикулярно мгновенному радиусу вращения) в сторону, определяемую угловым ускорением ε.

Угловое ускорение первого звена = 0, поскольку ω₁ = const.Следовательно = 0. Отсюда:

n

a_B1 = a_B1 .

И з произвольно выбранной точки P_a - полюса плана ускорений – проводим прямую, параллельную BА и в направлении от В к А откладываем отрезок P_ab₁, изображающий вектор абсолютного ускорения (рис. 2.8).

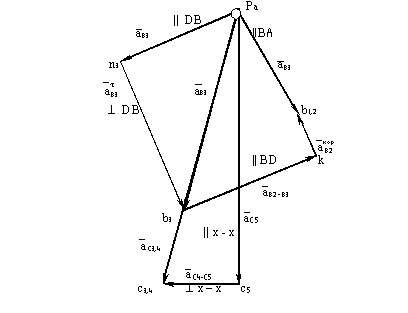
Рисунок 2.8 – План ускорений кулисного механизма

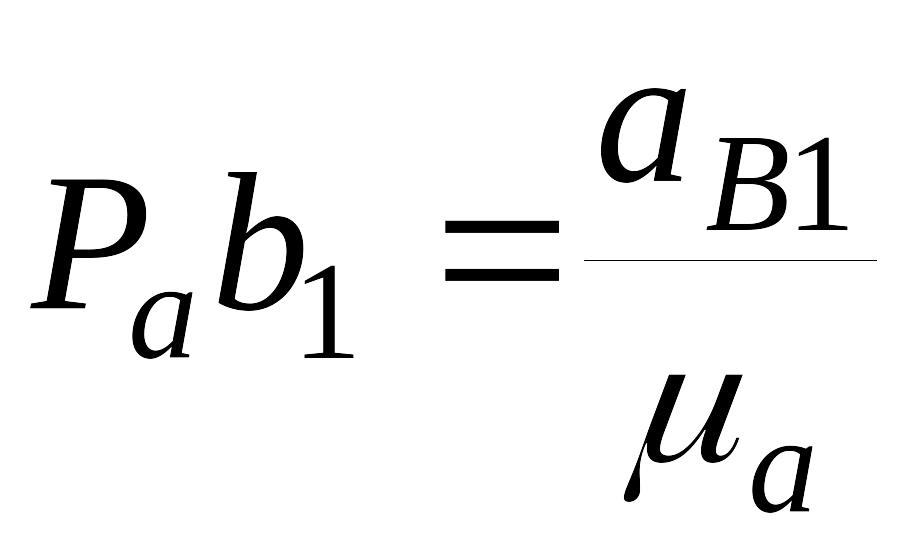
Дальнейшее построение плана ускорений механизма будем выполнять с учетом выбранного масштабного коэффициента μ_a.

Определяем ускорение точки B₂.

.

На плане ускорений изображается тем же отрезком, что и – P_ab_1,2.

О пределяем ускорение точки B₃. Для этого воспользуемся разложением сложного движения звена 2, как и при определении абсолютной линейной скорости V_B3:

пер отн кор

a_B2 = a_B2 + a_B2 +a_B2 . (2.26)

Абсолютное ускорение точки B₂ в сложном движении является векторной суммой переносного, относительного и кориолисова ускорений.

Переносное движение – возвратно-вращательное движение кулисы 3. Переносное ускорение точки B₂ камня равно абсолютному ускорению точки B₃ кулисы:

пер отн кор

a_B2 = a_B3 .

Звено 3 совершает возвратно-вращательное движение, поэтому абсолютное ускорение точки B₃ является векторной суммой нормального и тангенциального ускорений:

n τ

a_B3 = a_B3 + a_B3 .

n

В ектор нормального ускорения a_B3 направлен от В к D. Модуль нормального ускорения:

.

Вектор тангенциального ускорения направлен перпендикулярно DB. Модуль неизвестен.

Относительное ускорение в относительном движении направлено вдоль отрезка BD:

= .

|| BD

Кориолисово ускорение равно двойному векторному произведению угловой скорости переносного движения и линейной скорости относительного движения:

Угловая скорость переносного движения в нашем случае равна угловой скорости звена 3:

Относительная линейная скорость в нашем случае равна относительной скорости перемещения точки B₂ по отношению к точке B₃:

= .

Можно определить

= 2 .

Определяем модуль кориолисова ускорения:

= 2 ,

г де α – угол между направлениями векторов угловой ω₃ и линейной V_B2-B3 скоростей.

В нашем случае вектор угловой скорости ω₃ направлен перпендикулярно плоскости чертежа. Вектор относительной скорости V_B2-B3 лежит в плоскости чертежа. Угол между векторами угловой и относительной скоростей α = 90°,sin α = sin 90° = 1, следовательно:

Определяем направление вектора кориолисова ускорения по правилу Н.Е.Жуковского. Для этого необходимо вектор относительной скорости повернуть в направлении переносной угловой скорости на 90°. (Переносим V_{B2 -B3} на план механизма и поворачиваем его на 90° по направлению ω₃). В нашем случае a_B2  BD.

Подставим в исходное уравнение (2.9) полученные данные:

B D BD || BD BD

Получаем векторное уравнение с двумя скалярными неизвестными: модулями ускорений и . Решаем уравнение графическим методом. Из полюса плана ускорений P_a проводим линию параллельно BD – направление нормального ускорения точки B₃ - .

Определяем длину отрезка на плане ускорений:

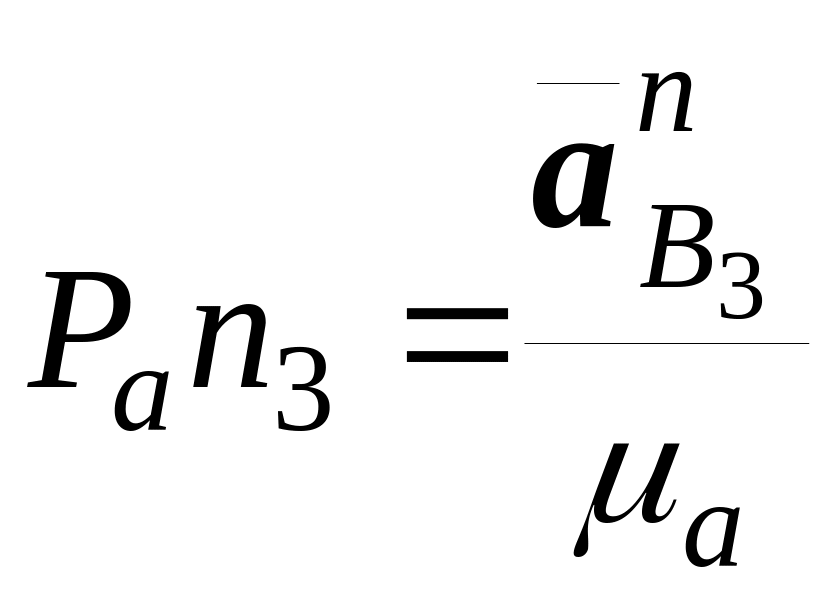
Откладываем отрезок P_an₃ и конец вектора обозначаем n₃. Через точку n₃ на плане ускорений проводим линию  BD (а следовательно и  P_an₃) – линию действия тангенциального ускорения .

Вектор является замыкающим в сумме векторов. Определим длину отрезка kb_1,2 = , откладываем отрезок на плане ускорений  BD и направляем вектор в точку b_1,2. Затем через точку k проводим параллельно BD линию действия вектора относительного ускорения , до пересечения с линией действия тангенциального ускорения . Полученную точку пересечения обозначаем b₃. Проставляем направление векторов и по правилу сложения векторов. Соединяем P_a с точкой b₃ на плане ускорений. Отрезок P_ab₃ является изображением абсолютного ускорения точки B₃ - . Определяем модули ускорений:

;

;

.

Определяем ускорение точки C₃, принадлежащей звену 3. Для этого воспользуемся теоремой подобия. Составляем пропорцию:

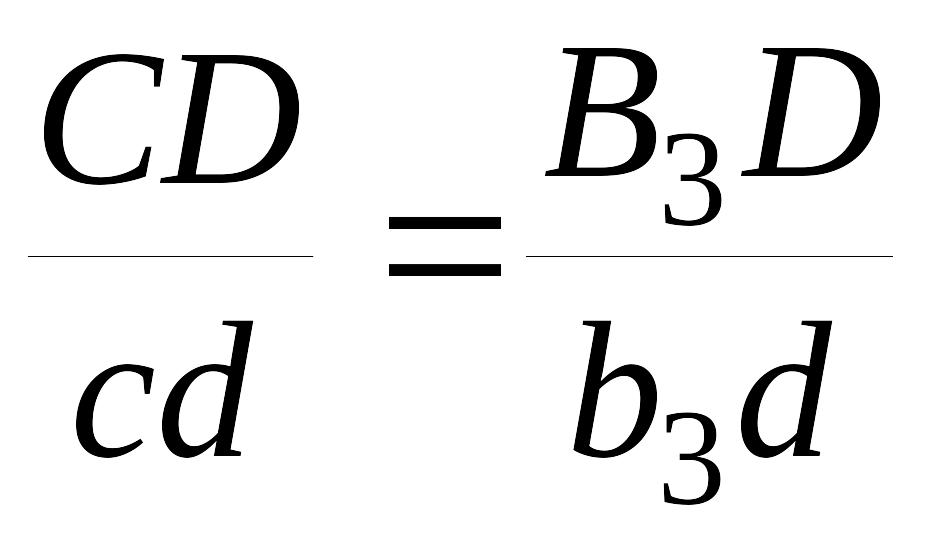
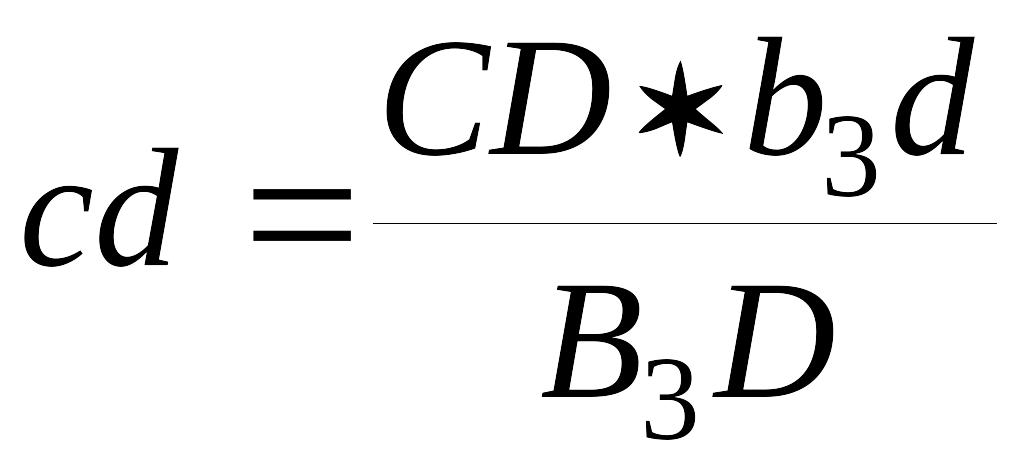
На продолжении отрезка P_ab₃ на плане ускорений откладываем отрезок P_ac₃ –

и зображениe вектора абсолютного ускорения точки C₃ - a_C3.

Определяем абсолютное ускорение точки C₅ – a_C5. Для этого воспользуемся предыдущим разложением сложного движения звена 4: переносное – поступательное параллельно оси х – х вместе с ползуном и относительное – поступательное перпендикулярно оси х – х. Составляем векторное уравнение ускорения точки C₄:

a_C4 = a_C5 + a_{C4 – C5}.

|| x-x  x-x

П олученное векторное уравнение имеет две скалярных неизвестных: модули ускорений a_C5 и a_{C4 – C5}. Решаем уравнение графическим методом. Из полюса P_a проводим линию параллельно х – х. Из точки с_3,4 проводим прямую перпендикулярно х – х. На пересечении этих прямых получаем точку C₅. Направление векторов проставляем в соответствии с правилом сложения векторов.

Определяем модули полученных ускорений:

a_C5 = (P_ac₅) μ_a ;

a_{C4 – C5} = (c_3,4c₅) μ_a .

Определяем угловые ускорения звеньев.

Угловое ускорение звена 1 – ε₁ = 0.

Угловое ускорение звена 2 равно угловому ускорению звена 3:

ε₂ = ε₃.

Угловое ускорение звена 3:

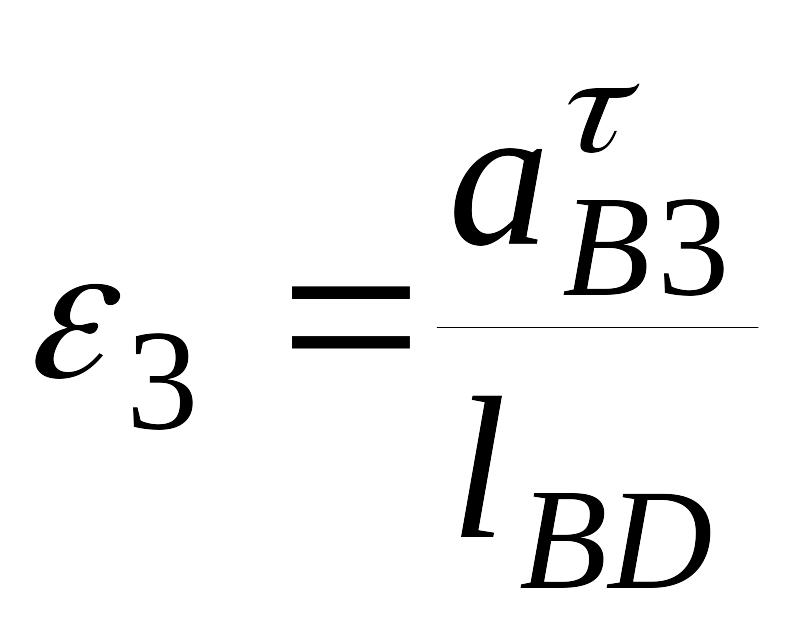
и направлено в сторону, определяемую направлением вектора a_B3 .