9.4 Определение минимального радиуса теоретического профиля кулачка. (Динамический синтез)

При рассмотрении углов давления α и углов передачи движения γ в кулачковых механизмах мы определили, что соотношение углов α и γ меняется по профилю кулачка (изменяется направление касательной в каждой точке профиля кулачка). При проектировании кулачкового механизма необходимо, чтобы угол давления не превышал некоторый заданный по условию не заклинивания или другим условиям угол давления α _max

или .

Как видно из построения (рис.9.11), чем больше радиус кривизны кулачка в точке касания профиля кулачка с толкателем, тем меньше угол давления.

При конструировании кулачковых механизмов стремятся к уменьшению габаритов кулачка и всего механизма в целом. Поэтому стремятся получить минимальные радиусы кривизны профиля кулачка. Это улучшает весогабаритные показатели механизма и его динамические свойства. Очевидно, для каждого кулачкового механизма можно определить минимальный радиус профиля r₀, при котором еще будет удовлетворяться условие α≤α _max . Все другие радиусы профиля кулачка меньшие этого минимального не будут удовлетворять условию α≤ α _max.

Рассмотрим выбор минимального радиуса кулачка для механизма с вращающимся кулачком и поступательно движущимся толкателем (рис.9.11).

Скорость точки В конца толкателя ( ) представим как векторную сумму 2-х скоростей - переносную и относительную. Движение толкателя рассматриваем как переносное - вместе с кулачком и относительное - скольжение по профилю кулачка. Тогда абсолютная скорость конца толкателя будет представлена векторным уравнением:

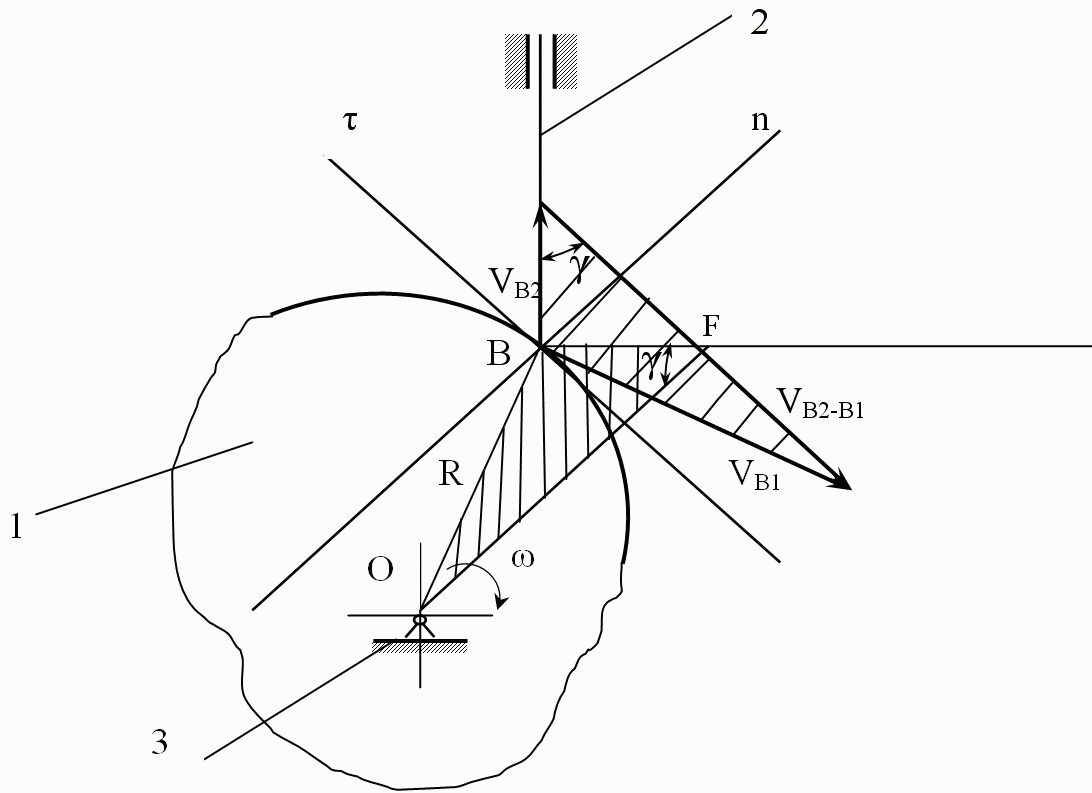
Рисунок 9.11 – К выбору r_о теоретического профиля кулачка

Вектор скорости точки В₂ толкателя направлен по оси толкателя в сторону перемещения толкателя.

Вектор переносной скорости точки В кулачка направлен перпендикулярно радиусу вращения ОВ в сторону угловой скорости кулачка ω и по модулю равен .

Вектор относительной скорости направлен по касательной к траектории точки В в относительном движении точки - скольжении по профилю кулачка, а, следовательно, по касательной τ-τ к профилю кулачка через точку контакта В. Решив векторное уравнение, определим все скорости по модулю и направлению их векторов.

Обозначим угол между направлением вектора абсолютной скорости точки В толкателя и касательной τ-τ – γ угол передачи движения в точке В профиля кулачка.

Выполним дополнительные построения. Из точки В в сторону вращения кулачка проведем перпендикуляр к скорости толкателя V_В , а из точки О — центра вращения кулачка проведем перпендикуляр к касательной τ-τ до пересечения с предыдущим перпендикуляром. Точку пересечения обозначим F. Рассмотрим треугольник скоростей и треугольник ОBF. Они подобны, т.к. их стороны взаимно перпендикулярны , , . Отрезок FB обозначим Z. Составим отношение:

; откуда 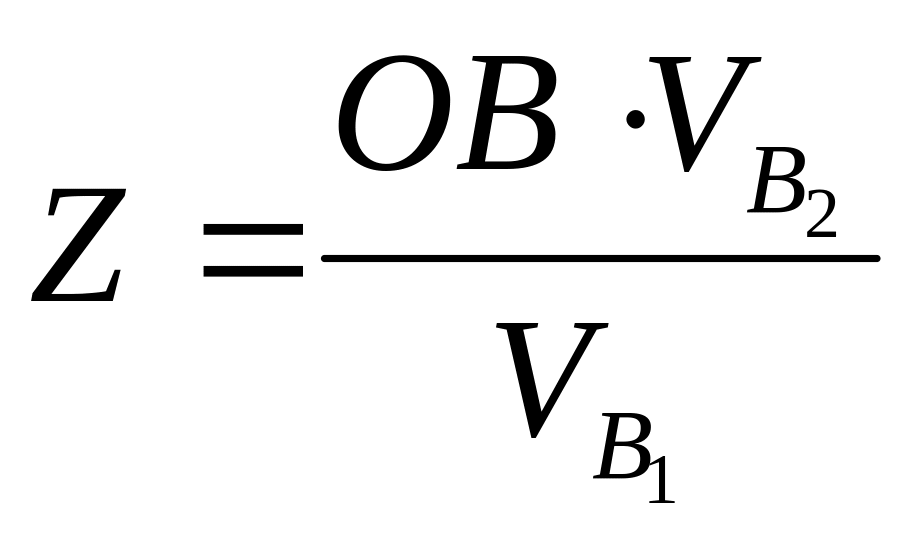, здесь ,

; заменим ; ,

тогда (аналог линейной скорости толкателя).

(9.15)

Следовательно, отрезок Z равен аналогу линейной скорости толкателя . Угол BFO равен углу передачи движения γ (их стороны взаимно перпендикулярны)

Из рисунка видно, что при увеличении отрезка ОB и неизменном Z угол γ будет увеличиваться и при уменьшении ОB — уменьшаться. Отрезок ОB — радиус кулачка в данной точке профиля кулачка B. Таким образом, при заданном γ_min можно определить r₀, имея аналог скорости толкателя .

Отметим, что положение точки F (слева или справа от линии толкателя) определяется вектором , если его повернуть на прямой угол в направлении вращения кулачка.

Приходим к следующему положению: если рассчитать отрезок Z= и отложить его на перпендикуляре к скорости конца толкателя в определенном направлении (V_B2 необходимо повернуть на 90⁰ по направлению вращения кулачка), конец отрезка соединить с центром кулачка, то угол между проведенным лучом и отрезком Z окажется равным углу передачи движения γ.

Если отрезки Z рассчитаны для нескольких положений толкателя на фазе удаления и фазе возвращения, то найти минимальный радиус профиля кулачка можно следующим образом.

С учетом масштабного коэффициента μ_ℓ изображается максимальное перемещение толкателя и на нем откладываются отрезки, изображающие перемещение толкателя в рассчитанном i-том положении (рис.9.12). По имеющимся значениям перемещения толкателя S(φ) и аналога скорости толкателя строится кривая . Для этого через полученные точки i-го перемещения толкателя, проводятся прямые, перпендикулярные траектории конца толкателя, на которых откладываются отрезки Z с учетом масштабного коэффициента μ₁ 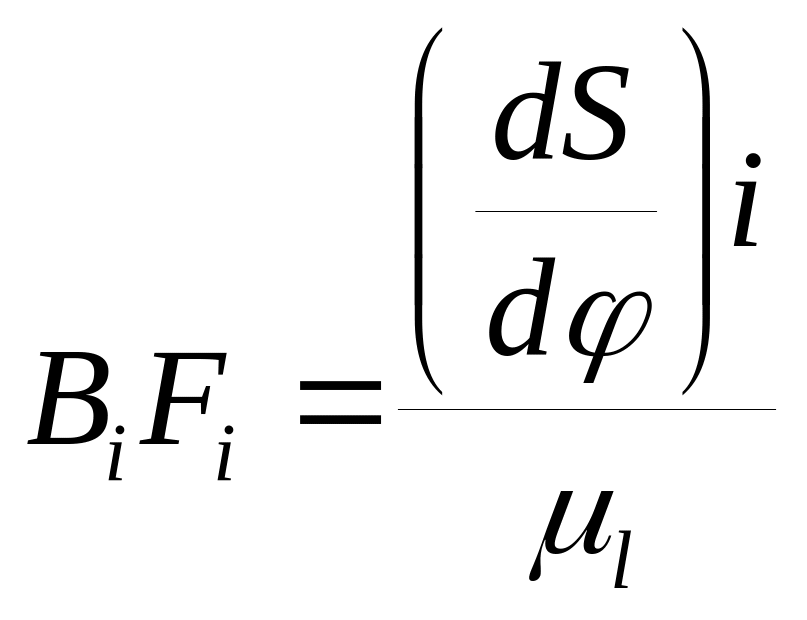. При этом положительные значения совпадают с направлением положительной скорости толкателя V_B2, повернутой на 90⁰ в сторону вращения кулачка. Точки М_i соединяются плавной кривой по лекалу.

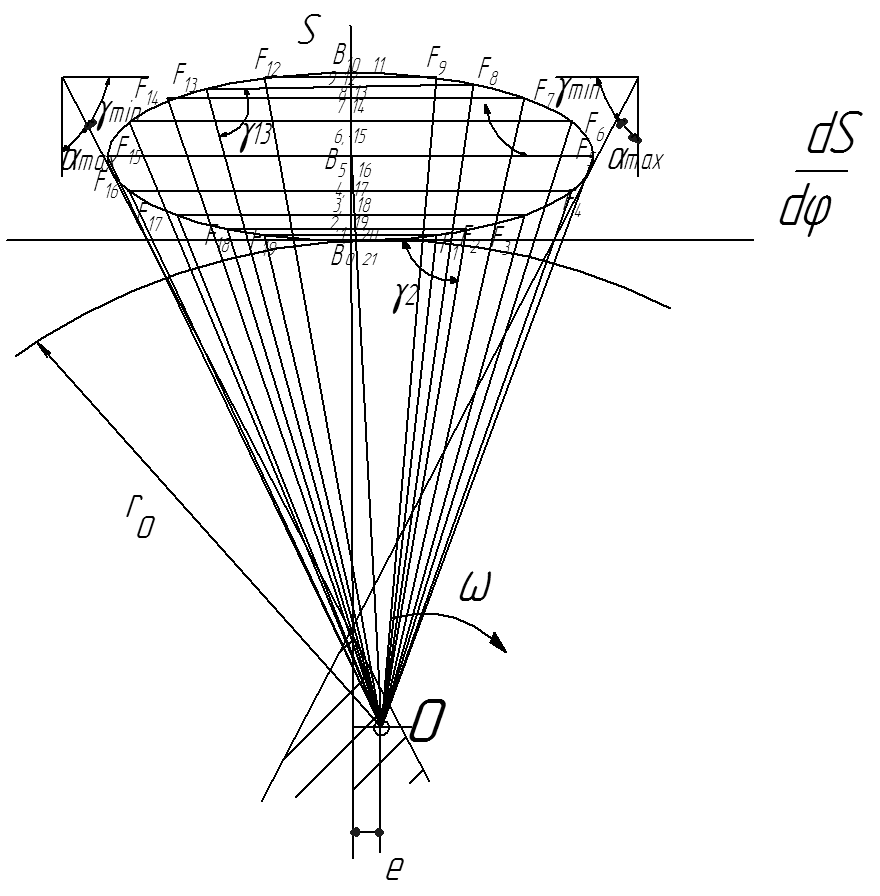
Рисунок 9.12 – К выбору r_o для кулачка с геометрическим замыканием

Под углом γ_min горизонтальной оси или α_max к вертикальной оси проводятся две касательные к построенной кривой. Пересекаясь, эти касательные ограничивают часть плоскости (между касательными за точкой их пересечения). Любая точка, лежащая в этой области может служить центром вращения кулачка, так как тогда в любом положении кулачкового механизма действительный угол передачи движения γ окажется меньше γ_min.

Если механизм нецентральный (имеет эксцентриситет), тогда от линии движения толкателя с учетом μ₁ откладывается эксцентриситет e и проводится прямая, параллельная траектории толкателя. На этой прямой в разрешенной области выбирается центр вращения кулачка О. Отрезок ОВ_o изображает минимальный радиус центрового профиля кулачка r₀. Если е=0, то точка о берется на линии S в разрешенной зоне.

Затем выбранный центр О соединяется с точками F и измеряются острые углы действительные углы передачи движения. Для соответствующих расчетных положений кулачкового механизма строится график γ(φ).

Если кулачковый механизм с силовым замыканием, то зависимость = f(S) строится только для фазы удаления.

Один ограничивающий луч под углом γ_min к горизонтали проводится как касательная к построенной кривой, другой — из точки В_о к горизонтали (рис.9.13) .

Рассмотрим порядок определения минимального радиуса вращающегося кулачка в механизме с вращающимся толкателем.

Построим механизм в произвольном положении (рис.9.13). Произведем построение, аналогичное тому, которое мы выполнили при определении Z в механизме с поступательно движущимся толкателем.

.

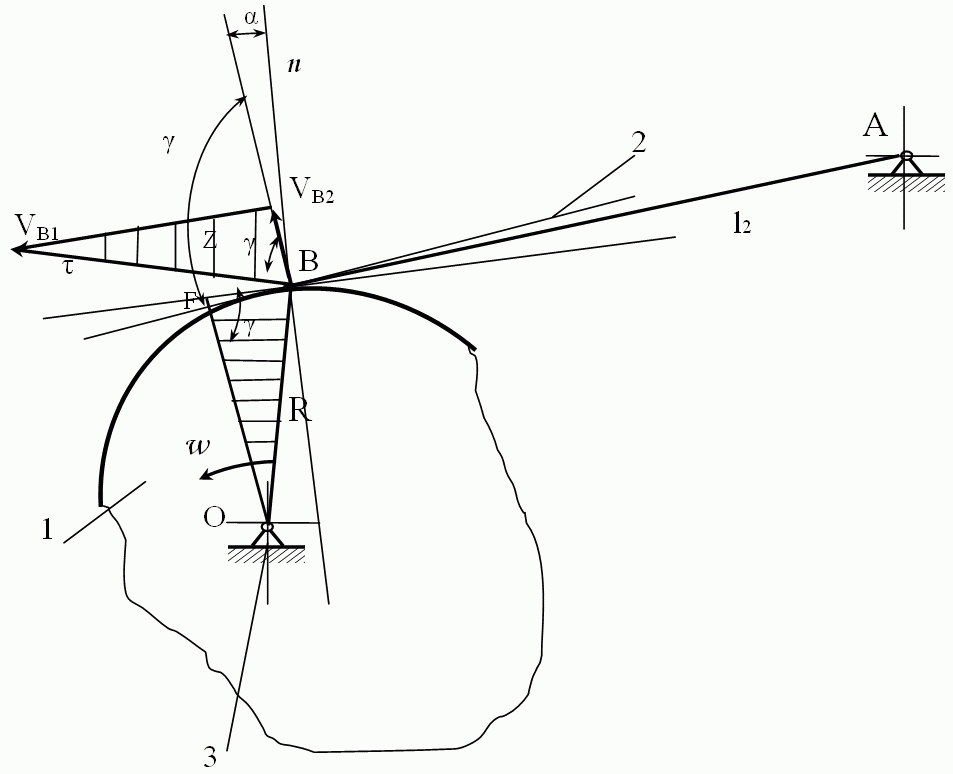
Рисунок 9.13 - Определение минимального радиуса вращающегося кулачка

в механизме с вращающимся толкателем

Скорость конца толкателя разложим на 2 скорости: переносную - скорость кулачка , и относительную - скорость перемещения конца толкателя по профилю кулачка.

Проведем линию перпендикулярную скорости толкателя в точке В и через O перпендикулярно ττ до пересечения с предыдущей линией. Точку их пересечения обозначим F. Получим треугольник ОBF подобный треугольнику скоростей. Угол BОF равен углу γ вследствие перпендикулярности сторон.

; ; ; ;

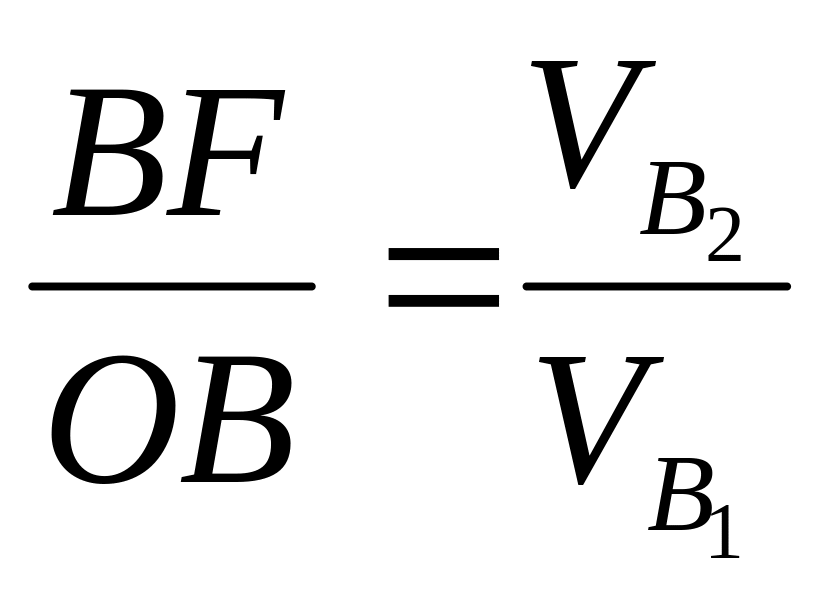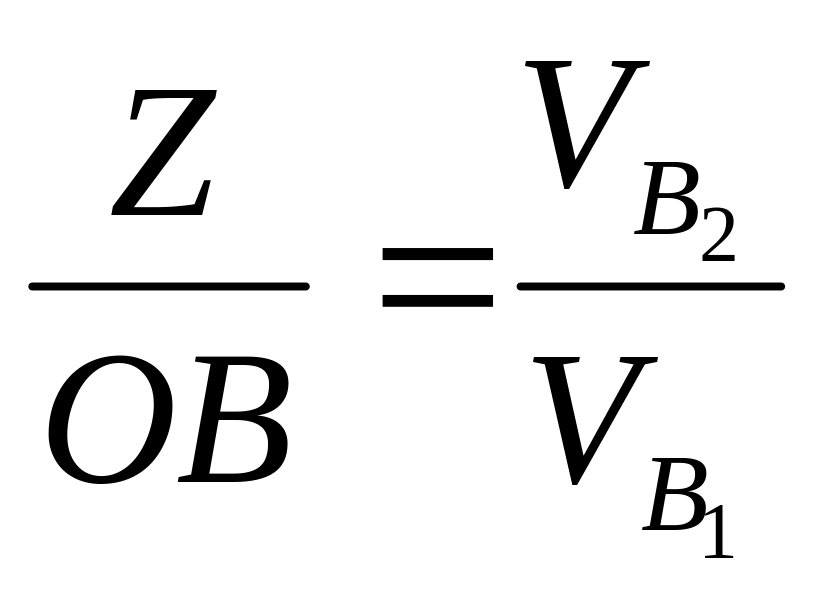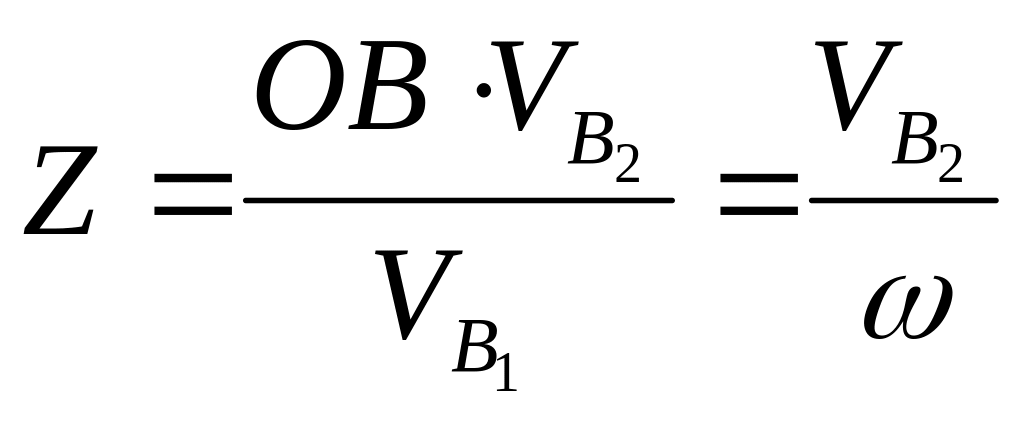, откуда .

Таким образом, приходим к следующему выводу: если рассчитать отрезок Z и отложить его по перпендикуляру к скорости конца толкателя в сторону вращения кулачка (по повернутому на 90^о вектору скорости толкателя), то, соединив конец отрезка Z с центром кулачка, получим угол передачи движения между отрезком Z и лучом, соединяющим конец отрезка Z с центром кулачка.

Выбор минимального радиуса центрового профиля кулачка, исходя из динамического условия γ_i>γ_min, можно выполнить следующим образом. Изображается толкатель в начальном положении АВ_o с учетом масштабного коэффициента длины μ₁. Проводится дуга окружности АВ_o, и откладывается угол β_max (рис.9.14). На дуге намечаются точки B₁, B₂, B₃ … B_n таким образом, чтобы угол B_oАB_i= β_i. Значения углов поворота толкателя β_i найдены ранее, при определении законов движения толкателя. Точки соединяются с центром вращения кулачка В. Далее во всех указанных положениях толкателя вдоль линии толкателя в определенном направлении (которое определяется поворотом вектора скорости конца толкателя на 90^o в сторону вращения кулачка) от точки B_i; откладываются подсчитанные отрезки B_iF_i(Z) с учетом масштабного коэффициента μ_l .Точки F_i соединяют плавной кривой .

Через каждую точку F_i под углом γ_min к соответствующему положению толкателя проводят прямые, которые, пересекаясь, образуют область возможного расположения центра вращения кулачка. Выбранная точка O соединяется с центром вращения толкателя A. Размер ОA изображает межосевое расстояние l_OA. Отрезок ОB_o, является изображением минимального радиуса теоретического профиля кулачка.

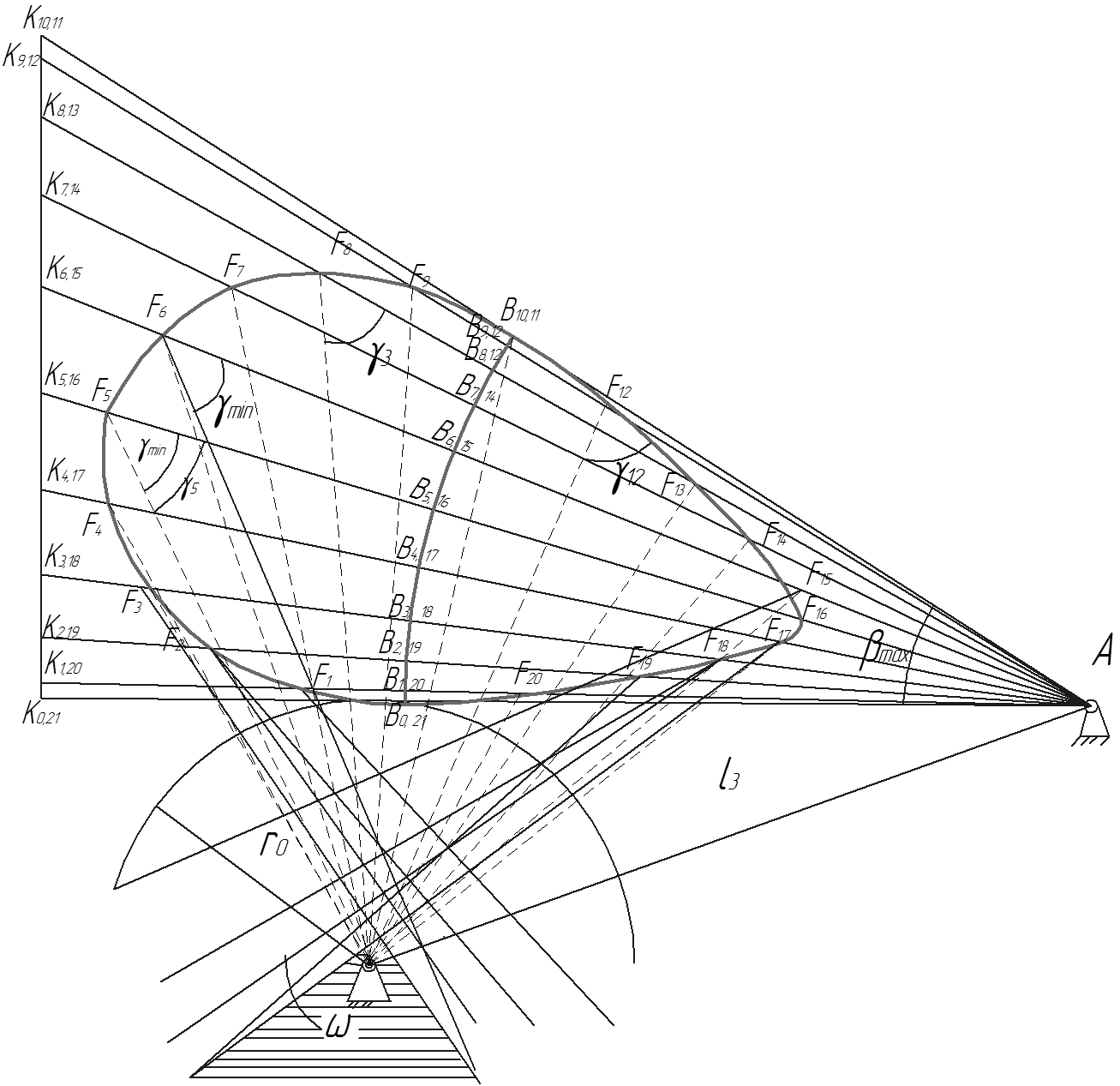
Рис.9.14 – К выбору r_o теоретического профиля вращающегося кулачка с

вращающимся толкателем

Если механизм с силовым замыканием (рис.9.15), то возвращение толкателя происходит под действием силы упругости пружины. В таком случае проводится построение только на этапе удаления. Кроме лучей из каждой точки F_i под углом γ_min проводится луч из точки Ао под углом γ_min и определяется область возможного положения центра кулачка О. Для более точного построения углов β_i пользуются значениями их тангенсов.

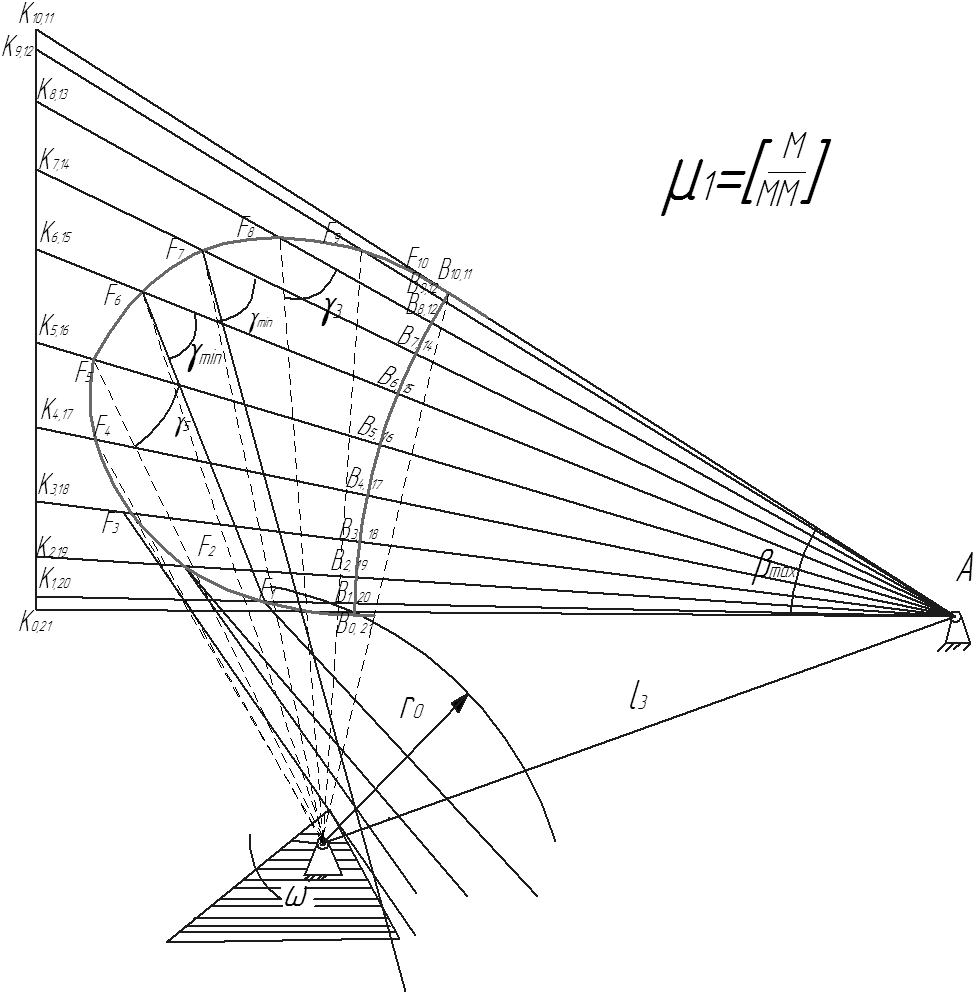
Рисунок 9.15 – К выбору r_o кулачкового механизма с силовым замыканием

замыканием и вращающимся толкателем