7. Минимальный радиус кривизны эвольвенты.

Явление подрезания. Условие отсутствия подрезания

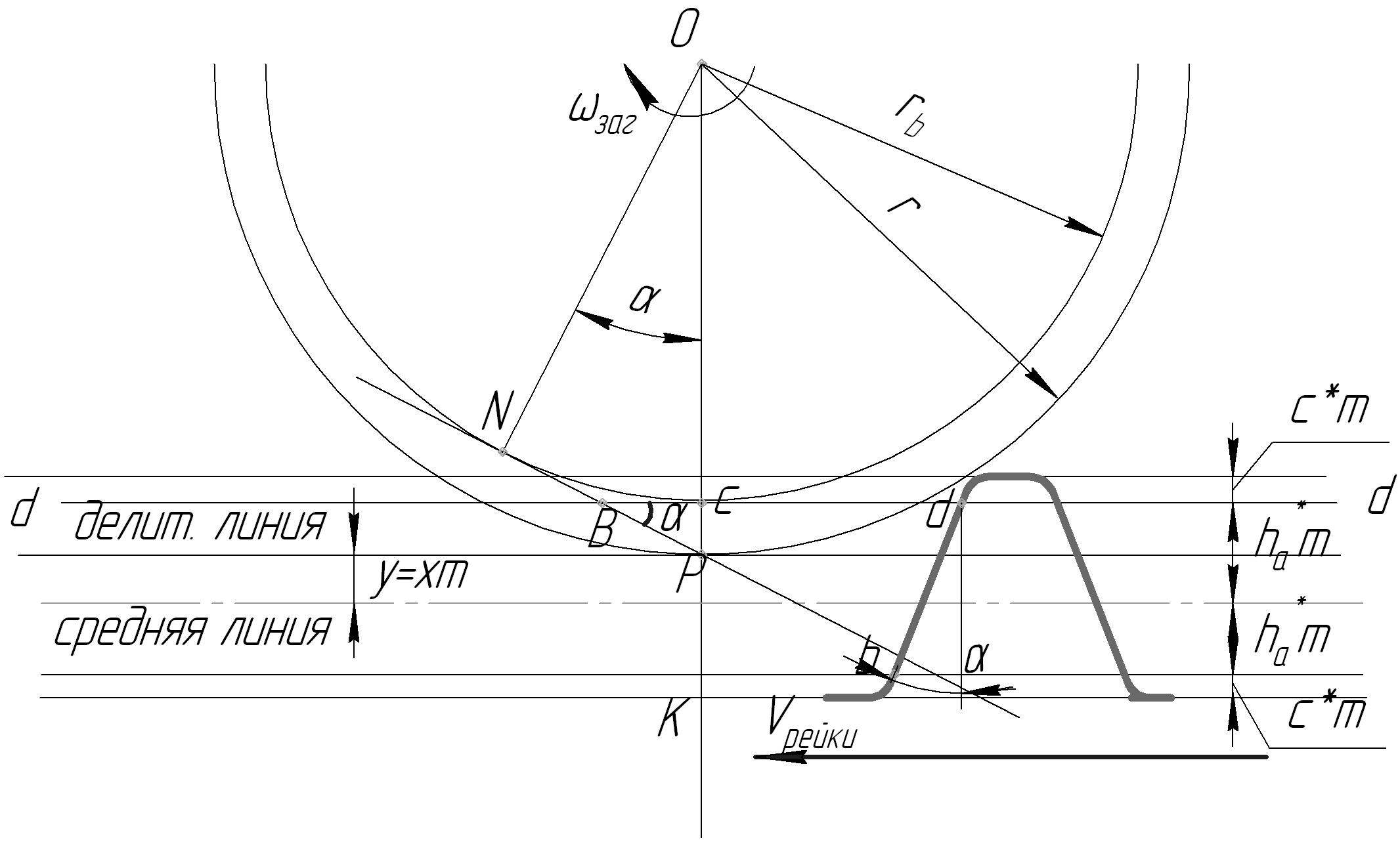
Рисунок 8.18 – К определению минимального радиуса

кривизны эвольвенты

При нарезании эвольвентных зубьев эвольвенту формирует прямолинейная часть профиля зуба инструмента ав – рисунок 8.18. Выше точки а переходной участок зуба инструмента нарезает галтель зуба колеса.

В процессе нарезания точка контакта перемещается по линии станочного зацепления NP. Траектория точки а рейки – это линия dd. Крайняя точка, в которой прямолинейный профиль зуба рейки контактирует с нарезаемым зубом колеса – это точка пересечения траектории точки а с линией станочного зацепления – точка В (рисунок 8.18). По свойствам эвольвенты линия NP является нормалью к нарезаемой эвольвенте и отрезок нормали от эвольвенты до точки касания ее с основной окружностью является радиусом кривизны эвольвенты.

Поскольку точка В является крайней точкой контакта прямолинейного профиля зуба инструментальной рейки с нарезаемой эвольвентой зуба колеса, то отрезок NB является минимальным радиусом кривизны эвольвенты - _min :

_min = NB.

При нарезании возможны три варианта :

1. Траектория точки а, т.е. линия dd проходит ниже точки N, тогда _min> 0.

Этот вариант изображен на рисунках 8.18 и 8.19а. В этом случае эвольвента недорезается до основной окружности. От точки В до основной окружности будет нарезаться не эвольвентный профиль зуба, а переходная кривая, изображенная тонкой линией на рисунке 8.19а.

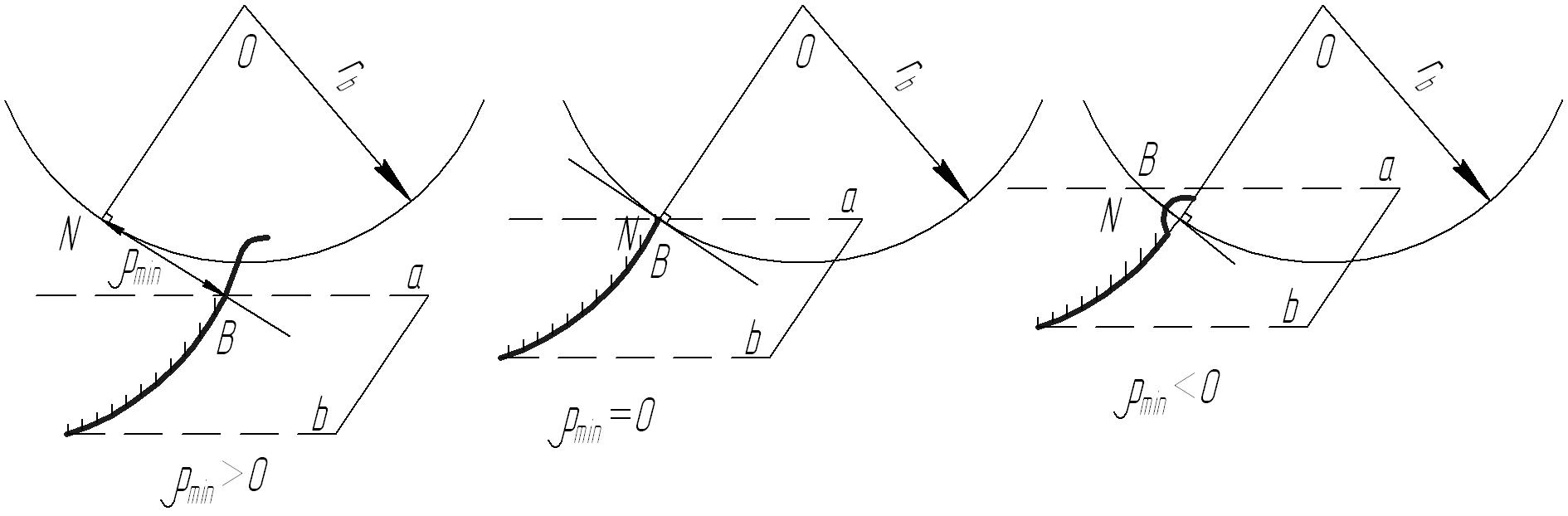
Рисунок 8.19 – Варианты нарезания эвольвентного профиля зуба

2. Траектория точки а проходит через точку N, тогда _min=NB =0. В этом случае эвольвента зуба начинается с основной окружности – рисунок 8.19б.

3. Траектория точки а проходит выше точки N, тогда _min<0. В этом случае эвольвента нарезается до основной окружности, а затем головка зуба рейки срезает часть эвольвентного профиля ножки нарезаемого зуба – рис. 8.19в.

Это явление называется подрезанием зуба. Подрезанная часть ножки зуба получается неправильной формы, кроме того, толщина зуба у его основания уменьшается, что приводит к снижению его изгибной прочности. Поэтому явления подрезания не должно быть.

Определим минимальный радиус кривизны эвольвенты _min. Из рисунка 8.18:

_min = NB = NP – BP.

Из треугольника ONP определим NP:

.

Из треугольника ВРС определим ВР:

.

Тогда

,

Или окончательно (8.24)

Ранее установлено, что подрезания зуба колеса не будет, если траектория крайней точки прямолинейного участка профиля зуба рейки проходит при поступательном ее движении не выше точки N (рисунок 8.19а,б), то есть если

_min  0 (8.25)

Это условие отсутствия подрезания зубьев.

Подставив в это условие значение _min, получим:

.

Так как m > 0, то получаем неравенство:

. (8.26).

Решив это уравнение относительно числа зубьев нарезаемого колеса z, получим:

(8.27)

Полученное выражение устанавливает связь между числом зубьев колеса z, и коэффициентом смещения х, при котором нет подрезания зуба. Если нарезается нулевое колесо, то есть х =0, стандартные параметры рейки ,  = 20⁰, то из выражения (8.27) получаем:

, , то есть .

Таким образом, минимальное число зубьев нулевого колеса, при котором не будет подрезания, равно 17. При z < 17 необходимо применять положительное смещение, причем минимальный коэффициент смещения по условию неподрезания также можно определить из выражения (8.26):

,

откуда (8.28)

Подставив и  = 20⁰, получаем:

(8.29)