8.6 Параметры эвольвентного колеса, нарезанного

инструментом реечного типа

Изобразим схему нарезания зубчатого колеса инструментом реечного типа (рисунок 8.16) и определим размеры нарезаемого колеса.

Заготовка вращается со скоростью _заг, а инструментальная рейка движется поступательно со скоростью V_рейки – это реечное станочное зацепление.

На линии ОК существует такая точка Р, в которой линейные скорости заготовки и рейки одинаковы:

. (8.13)

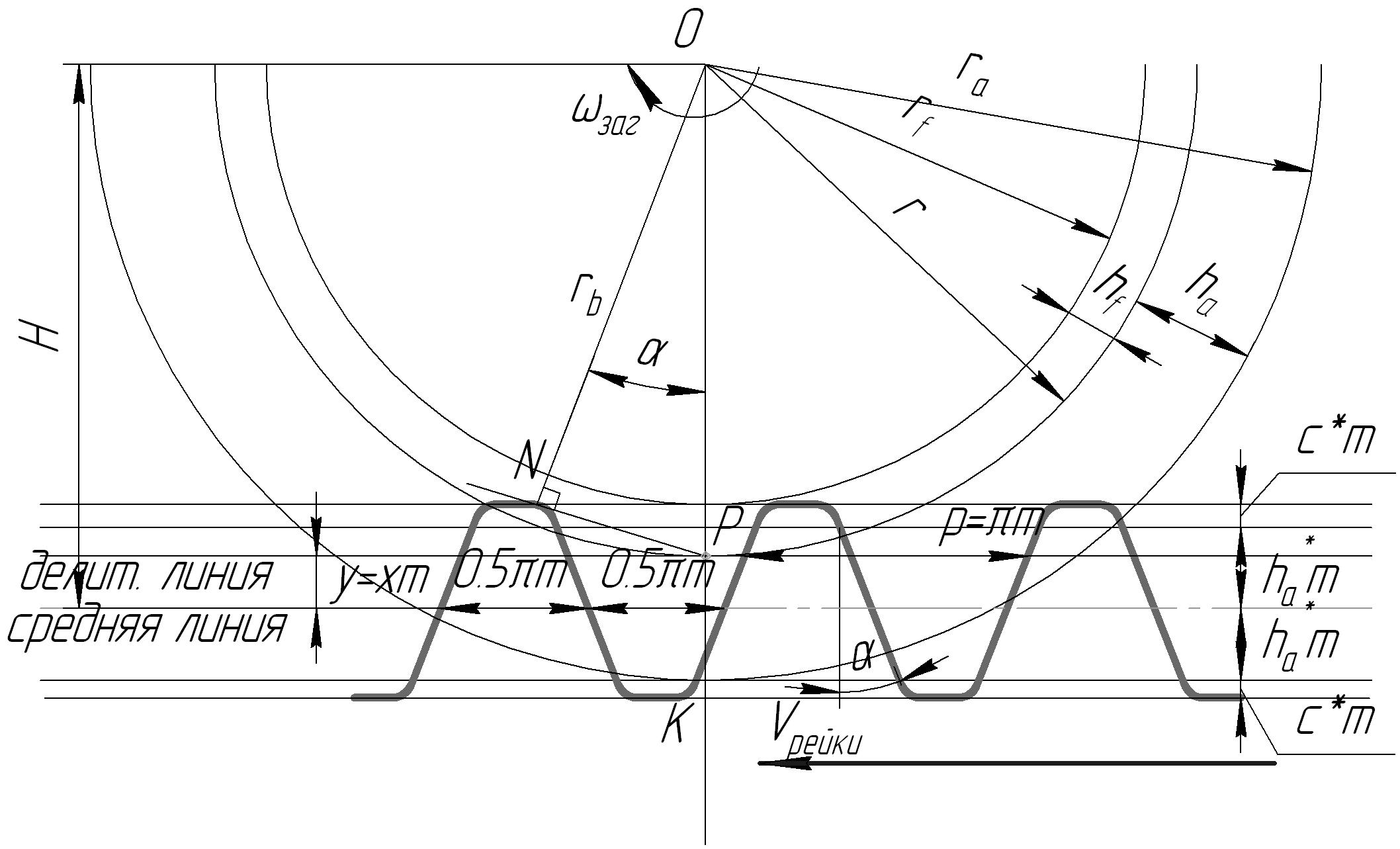
Рисунок 8.16 – Схема нарезания эвольвентного колеса инструментом

реечного типа

делительной линии рейки переносятся на делительную окружность колеса без искажения. Следовательно, шаг по делительной окружности равен стандартному шагу исходного контура Р = m. Радиус делительной окружности обозначается r.

Длина делительной окружности: 2r = рz, где z – число зубьев нарезаемого колеса; подставим значение р: 2r = mz, откуда

r = 0,5mz (8.14)

Линия NP, проходящая через точку Р перпендикулярно боковому профилю зуба рейки и к нарезаемой эвольвенте, является касательной к основной окружности. Это линия станочного зацепления. Следовательно, перпендикуляр ON, является радиусом основной окружности нарезаемого колеса – r_b, а угол NOP – угол станочного зацепления, он равен профильному углу рейки, т.е.  = 20⁰. Из треугольника ONP получаем:

r_b = rcos, r_b = 0,5mzcos (8.15)

Расстояние между и делительной линиями рейки «у» называется смещением рейки.

Отношение смещения рейки к модулю называется коэффициентом смещения:

(8.16)

Обозначим расстояние от центра заготовки до средней линии рейки –Н (рис.8.16) При нарезании зубчатого колеса возможны три варианта установки инструмента, т.е рейки относительно центра заготовки:

1. H=r, y=0, x=0 – нарезается нулевое колесо – колесо без смещения. При этом средняя линия рейки катится без скольжения по делительной окружности заготовки, толщина зуба по делительной окружности равна ширине впадины.

2. H>r, y>0, x>0 – нарезается колесо с положительным смещением. Рейка отодвинута от центра заготовки, толщина зуба по делительной окружности больше ширины впадины.

3. H<r, y<0, x<0 – нарезается колесо с отрицательным смещением. Рейка придвинута к центру заготовки. Толщина зуба по делительной окружности меньше ширины впадины.

Делительная окружность делит зуб колеса по высоте на два участка, называемые головкой и ножкой зуба. Часть зуба, расположенная вне делительной окружности, называется головкой зуба. Высота головки зуба обозначается h_а. Окружность, проходящая по вершинам головок зубьев, называется окружностью вершин колеса. Радиус окружности вершин обозначается r_а. По рисунку 8.16 получаем:

(8.17)

, или окончательно

(8.18)

Отметим, что радиус окружности вершин может определяться и из других соображений (см. п. 8.11).

Часть зуба, расположенная внутри делительной окружности, называется ножкой зуба. Высота ножки зуба обозначается h_f. Окружность, проходящая по основаниям ножек зубьев, называется окружностью впадин. Радиус окружности впадин обозначается r_f. По рисунку 8.16 :

(8.19)

,

(8.20)

Определим толщину зуба S и ширину впадины е нарезаемого колеса по делительной окружности. Зуб колеса формируется впадинами инструмента, поэтому (рисунок 8.17) : e_u=S, S_u=e, где

S_u и e_u – размеры на инструменте, а S и e – на нарезаемом колесе.

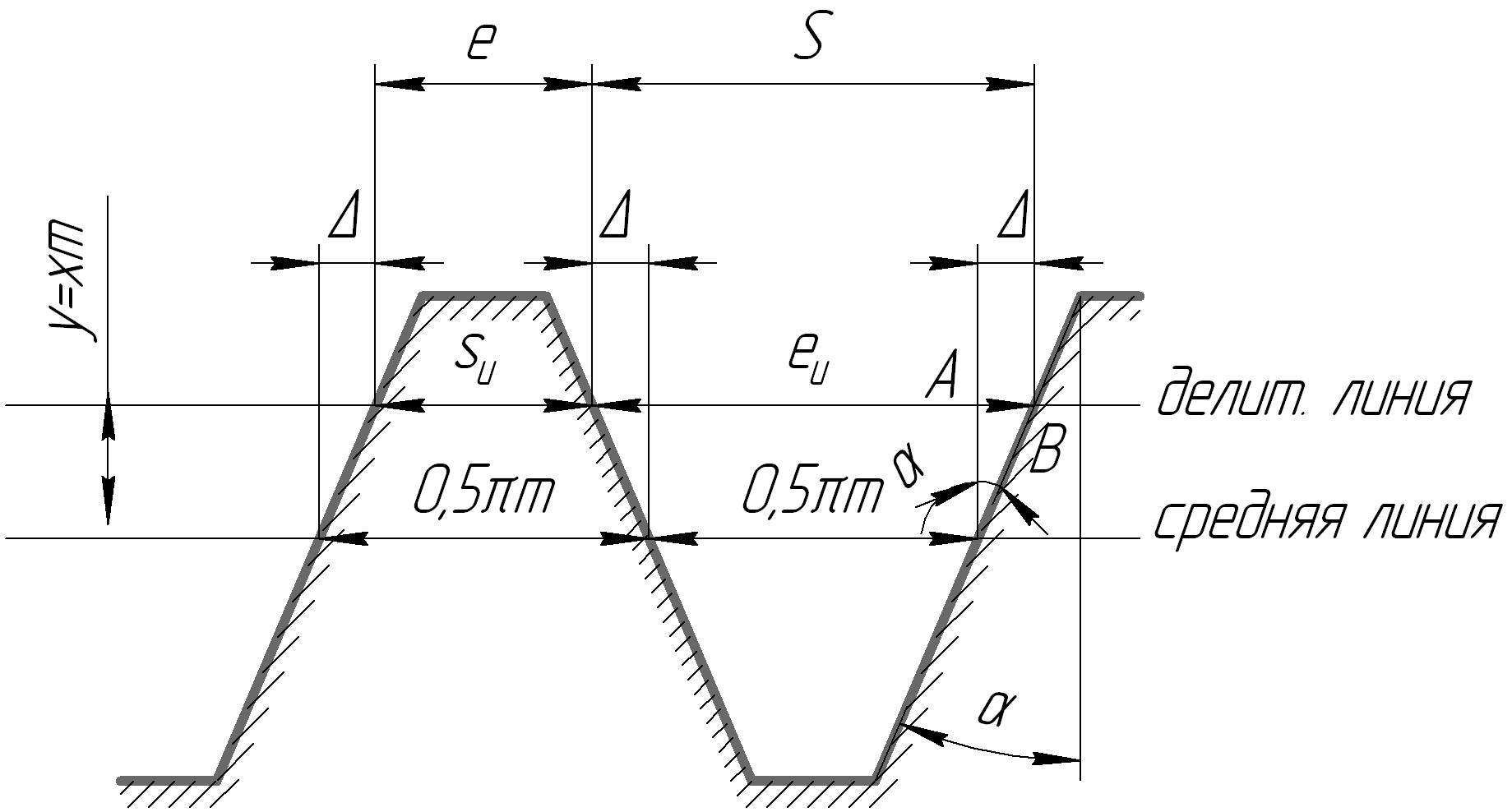
Рисунок 8.17 – К определению толщины зуба S и ширины впадины е

Так как при нарезании нулевого колеса все размеры со средней линии рейки переносятся на делительную окружность колеса без искажения, то у нулевого колеса по делительной окружности получаем:

S=e= 0,5m (8.21)

При нарезании колеса со смещением у=x m размеры с делительной линии переносятся на делительную окружность колеса без искажения, следовательно, у колеса со смещением S e.

Согласно рисунку 8.17 имеем : S=0,5m +2.

Отрезок  определим из прямоугольного треугольника АВС :

 = уtg =xmtg.

Тогда получаем толщину зуба по делительной окружности :

S = m(0,5+2xtg) (8.22)

Аналогично, ширина впадины по делительной окружности :

e = 0,5m - 2,

e =m(0,5 - 2xtg). (8.23)

В формулах (8.16 – 8.23) коэффициент смещения – величина алгебраическая, то есть х имеет знак + при положительном смещении рейки и  -  при отрицательном смещении.

Из формулы (8.22) следует, что при положительном смещении толщина зуба колеса по делительной окружности увеличивается по сравнению с нулевым колесом, а при отрицательном смещении – уменьшается. Следовательно, положительное смещение инструмента приводит к упрочнению зуба колеса, что часто используется в зубчатых передачах, передающие значительные мощности.