3. Эвольвентное реечное зацепление. Исходный контур

эвольвентных зубчатых колёс

Эвольвентное реечное зацепление представляет собой зацепление эвольвентного колеса с эвольвентной рейкой и предназначено для преобразования вращательного движения зубчатого колеса в поступательное движение рейки и наоборот.

Выясним, какой профиль имеет зуб эвольвентной рейки, находящейся в правильном зацеплении с эвольвентным колесом.

Изобразим зацепление двух эвольвентных колес с центрами О₁ и О₂ и радиусами основных окружностей r_b1 и r_b2 . Проведем межосевую линию О₁ и О₂ и общую касательную к основным окружностям N₁N₂ (рисунок 8.10). На пересечении О₁О₂ и N₁N₂ получим точку Р – полюс зацепления.

Пусть эвольвента первого колеса Э₁ зацепляется с эвольвентой второго колеса Э₂ в полюсе Р. Тогда радиус кривизны эвольвенты Э₁ в точке Р равен отрезку нормали N₁P , а радиус кривизны эвольвенты Э₂ в точке Р равен отрезку нормали N₂P:

_э1 = N₁P , _э2 = N₂P .

Предположим , что число зубьев первого колеса не изменяется (z₁ = const). Увеличим число зубьев второго колеса. При этом увеличится межосевое расстояние а_w. Точка О₂ займет новое положение – О₂. Увеличится радиус основной окружности r_b2. Увеличится отрезок PN₂ , так как точка N₂ займет новое положение N₂. Следовательно, увеличится радиус кривизны эвольвенты Э₂ в точке Р:

В пределе при увеличении z₂ до  центр второго колеса окажется в бесконечности и радиус кривизны эвольвенты Э₂ _э2 = . Эвольвента Э₂ превратится в прямую линию, перпендикулярную N₁N₂. Колесо 2 превратится в рейку.

Профиль зуба эвольвентной рейки является прямой линией, перпендикулярной линии зацепления, а сечение зуба – трапеция.

Начальная окружность колеса 2 превратилась в начальную прямую, катящуюся без скольжения по начальной окружности колеса 1. Угол между профилем рейки и перпендикуляром к начальной прямой – угол профиля – равен углу зацепления (по взаимной перпендикулярности сторон).

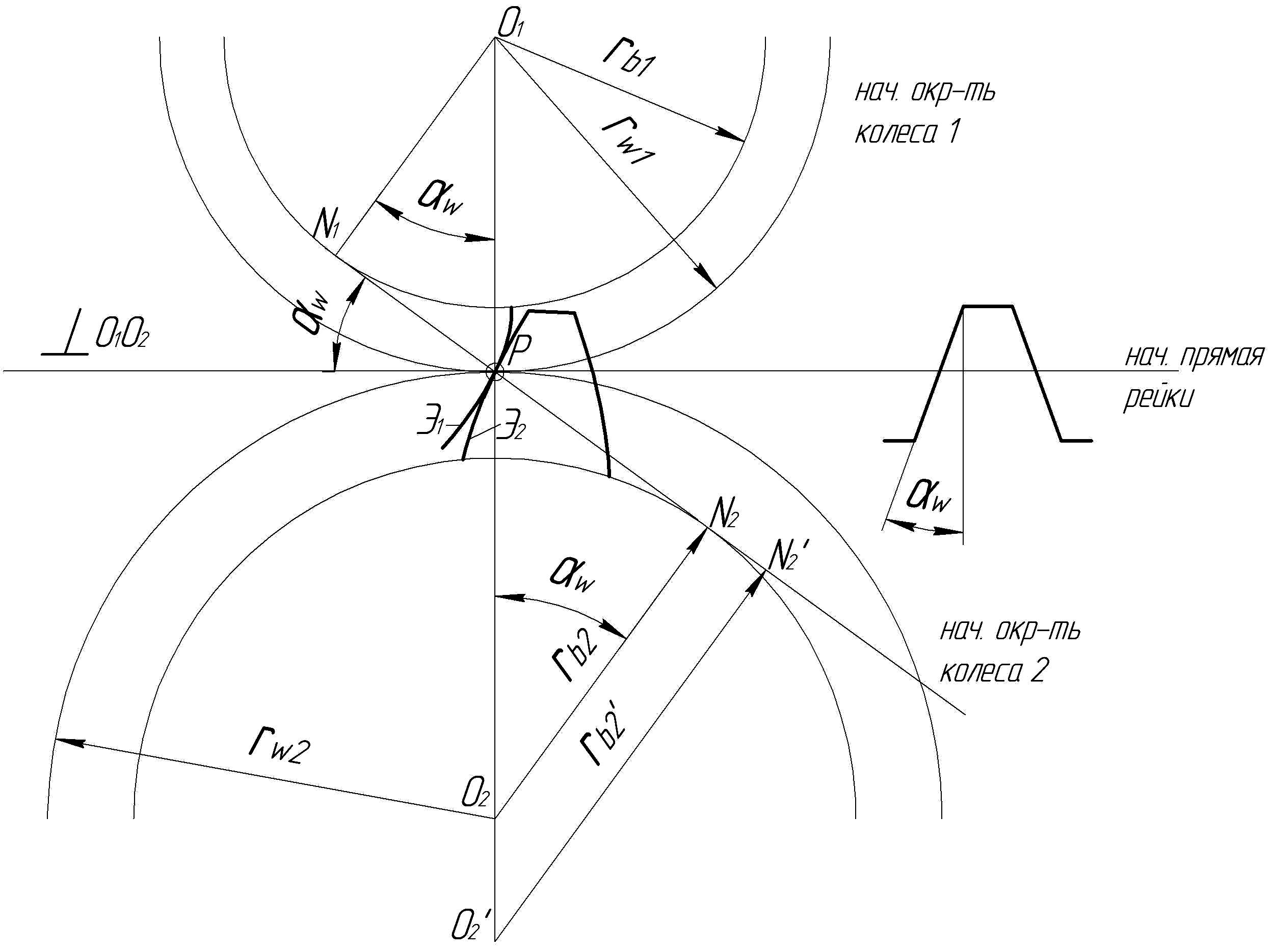
Рисунок 8.10 – Образование профиля эвольвентной рейки

Линия реечного зацепления – это прямая, проходящая через полюс зацепления по касательной к основной окружности колеса 1 перпендикулярно к профилю зуба рейки.

Эвольвентные зубчатые колеса стандартизованы. Стандартным является исходный контур эвольвентных колес, по которому выполняется инструмент для нарезания эвольвентных зубьев.

Исходным контуром эвольвентного колеса является контур зубьев эвольвентной рейки с определенными стандартными параметрами.

Изобразим эвольвентную рейку в соответствии с ГОСТом – рисунок 8.11. Проведем среднюю (модульную) линию исходного контура. Это линия, по которой толщина зуба рейки равна ширине впадины.

Расстояние между одноименными профилями двух соседних зубьев по любой линии, параллельной средней, называется шагом исходного контура и обозначается р. Отношение шага исходного контура к числу  называется модулем:

, следовательно . (8.12)

Модуль – это основной геометрический параметр, определяющий все размеры, исходного контура, а следовательно и эвольвентного колеса. Модуль имеет размерность “мм” и значения модуля стандартизованы. Величина модуля выбирается из стандартного ряда по условию прочности зубьев. Все остальные размеры исходного контура задаются в долях модуля.

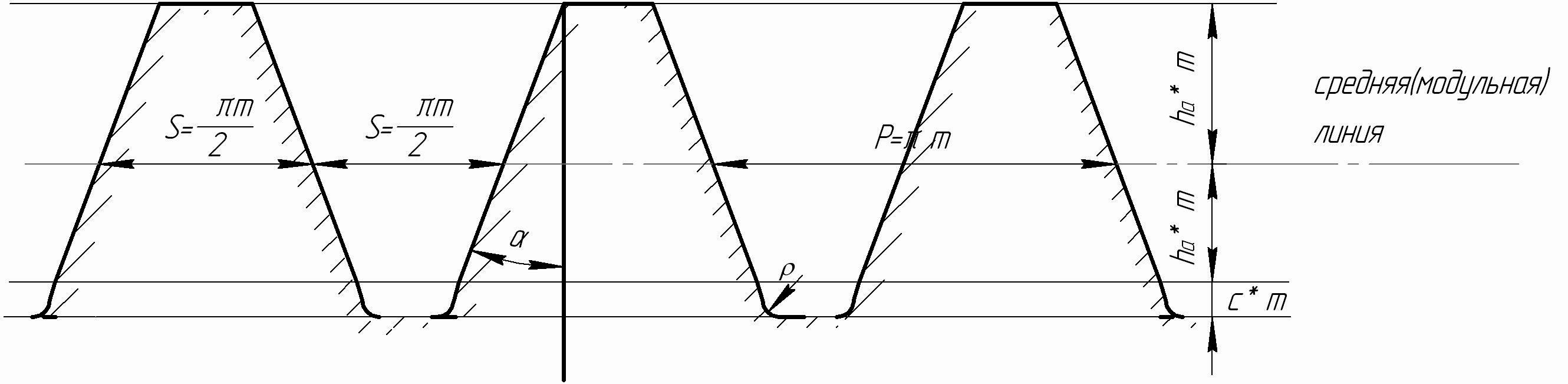
Рисунок 8.11 – Исходный контур эвольвентных колес

Разделив шаг р по средней линии пополам, получим толщину зуба ,ширину впадины .

Угол наклона бокового профиля зуба рейки к линии, перпендикулярной средней, называется профильным углом исходного контура (угол профиля).

Этот угол по ГОСТу обозначается  и стандартное его значение: =20⁰.

Прямолинейная часть бокового профиля зуба исходного контура CD делится средней линией по высоте на две равные части. Высота каждой из них равна , где - коэффициент высоты зуба. Переход от прямолинейной части зуба к основанию впадины осуществлен по дуге радиуса  = 0,38m. Эта скругленная часть зуба называется галтелью (выкружкой) зуба, высота которой равна c^*m, где с^* - коэффициент радиального зазора. Согласно стандарту , с^*= 0,25. ГОСТОм допускается еще одно сочетание значений , с^* =0,3.