8. Основы теории плоского эвольвенного зацепления

Значительное место среди различных входящих в состав машины механизмов,

занимают передаточные механизмы, осуществляющие передачу вращательного движения от двигателя к исполнительному механизму машины.

Широкое распространение в качестве передаточных механизмов получили зубчатые передачи, в которых движение передается высшей кинематической парой, элементами которой являются профили зубьев. Передача вращательного движения в зубчатой передаче осуществляется силой давления, возникающей в точке контакта профилей при перекатывании боковой поверхности зуба ведущего колеса по боковой поверхности зуба ведомого колеса.

Применение зубчатых колес имеет очень большую давность. В сочинениях древнегреческих философов (Платон «Государство», Аристотель «Механические проблемы») имеются сведения о применении в Греции за 3,5 века до нашей эры металлических зубчатых колес, у Паппа Александрийского (284-305 г.г.) описывается редуктор из зубчатых и червячных передач. В записках Леонардо да Винчи (1452-1519г.г.) описываются как цилиндрические, так и винтовые зубчатые колеса.

Леонард Эйлер, член Российской Академии наук, предложил и разработал в 1765 году теорию эвольвентного зацепления зубчатых колес, которая в настоящее время имеет широкое распространение [1].

Эвольвентные зубчатые колеса широко применяются в различных отраслях промышленности как в машинах, аппаратах, так и в измерительных приборах, автоматических регуляторах технологических процессов. Они передают вращательные движения от одного вала к другому, позволяя получить требуемую величину и направление угловой скорости выходного вала. Зубчатые механизмы, в которых происходит уменьшение угловых скоростей при передаче энергии от входного звена к выходному, называют редукторами. Зубчатые механизмы, в которых угловая скорость выходного звена увеличивается, называются мультипликаторами.

Так как зубчатые передачи являются важной составной частью большинства современных машин и многих приборов, большое значение имеет грамотное их проектирование [10].

При решении задач геометрического проектирования эвольвентного зубчатого зацепления необходимы знания основ теории зацепления, терминологии, основных зависимостей между геометрическими параметрами колес, методов правильного выбора исходных данных, которые наилучшим образом удовлетворяли бы конкретным условиям работы передачи и критериям качества зацепления. Все эти вопросы рассматриваются в данном разделе.

8.1. Основная теорема плоского зацепления

(Основной закон. Теорема Виллиса)

Под зацеплением понимают высшую кинематическую пару (т.е. контакт двух материальных тел по линии или в точке), в которой движение от одного тела к другому передается силой давления.

Понятие зацепления шире, чем контакт зубчатых колес. Это может быть и контакт кулачка с роликом, кулачка с толкателем, контакт двух любых криволинейных поверхностей. Будем рассматривать плоское зацепление. Плоским называется такое зацепление, в котором относительное движение звеньев плоское.

Основная теорема зацепления, которая была сформулирована Виллисом в 1841 году, устанавливает связь между кинематикой звеньев (угловыми скоростями) и геометрией контактирующих поверхностей (их формой). Теорема справедлива для двух звеньев, передающих движение силой давления. Рассмотрим случай, когда оба контактирующих тела совершают вращательное движение.

Пусть два произвольных профиля контактируют в данный момент времени в точке А (рис. 8.1.). При этом звено 1 совершает вращательное движение вокруг оси О₁ с угловой скоростью ₁ и передает движение звену 2, которое вращается с угловой скоростью ₂ вокруг оси О₂. Зацепление будем считать правильным.

Правильным называется такое зацепление, в котором контакт профилей существовал до рассматриваемого момента, существует в рассматриваемый момент и будет существовать после рассматриваемого момента.

Определим передаточное отношение от звена 1 к звену 2

Рассмотрим, как передаточное отношение связано с формой контактирующих поверхностей, т.е. с геометрией зацепления. Определим линейные скорости точки А, принадлежащей звену 1 и звену 2. Для этого соединим центры вращения О₁ и О₂ с точкой контакта звеньев А. Абсолютные скорости точек А₁ и А₂ направлены перпендикулярно к соответствующим радиусам вращения.

и (8.1.)

Так как точка А расположена не на межосевой линии О₁ и О₂, то линейные скорости точек и не совпадают по направлению. Это общий случай.

Через точку контакта профилей проведем общую нормаль n-n и большую касательную - к профилям и спроектируем на них абсолютные скорости точек и . Обозначим проекции скоростей на общую нормаль n-n соответственно С₁ и С₂, а на общую касательную - соответственно К₁ и К₂.

Точку пересечения нормали n-n с межосевой линией обозначим Р. С центров вращения О₁ и О₂ , а на общую нормаль проведем перпендикуляры О₁В₁ и О₂В₂. Углы между направлениями скоростей и и общей нормалью обозначим соответственно ₁ и ₂. Проанализируем связь между проекциями скоростей и на общую нормаль С₁ и С₂. Теоретически возможны следующие соотношения между С₁ и С₂:

1. Предположим, что С₁С₂. Тогда в следующий момент времени профиль 2 уйдет от профиля 1 и зацепление прервется, т.е. перестанет существовать кинематическая пара. Следовательно, по условию правильного зацепления проекции на общую нормаль С₁ не может быть меньше проекции на общую нормаль С₂.

2. Предположим, что С₁  С₂. Тогда в процессе работы профиль 1 должен обогнать профиль 2, что возможно только при деформации профилей, что по условиям работы кинематической пары недопустимо. Следовательно, С₁ не может быть больше С_2.

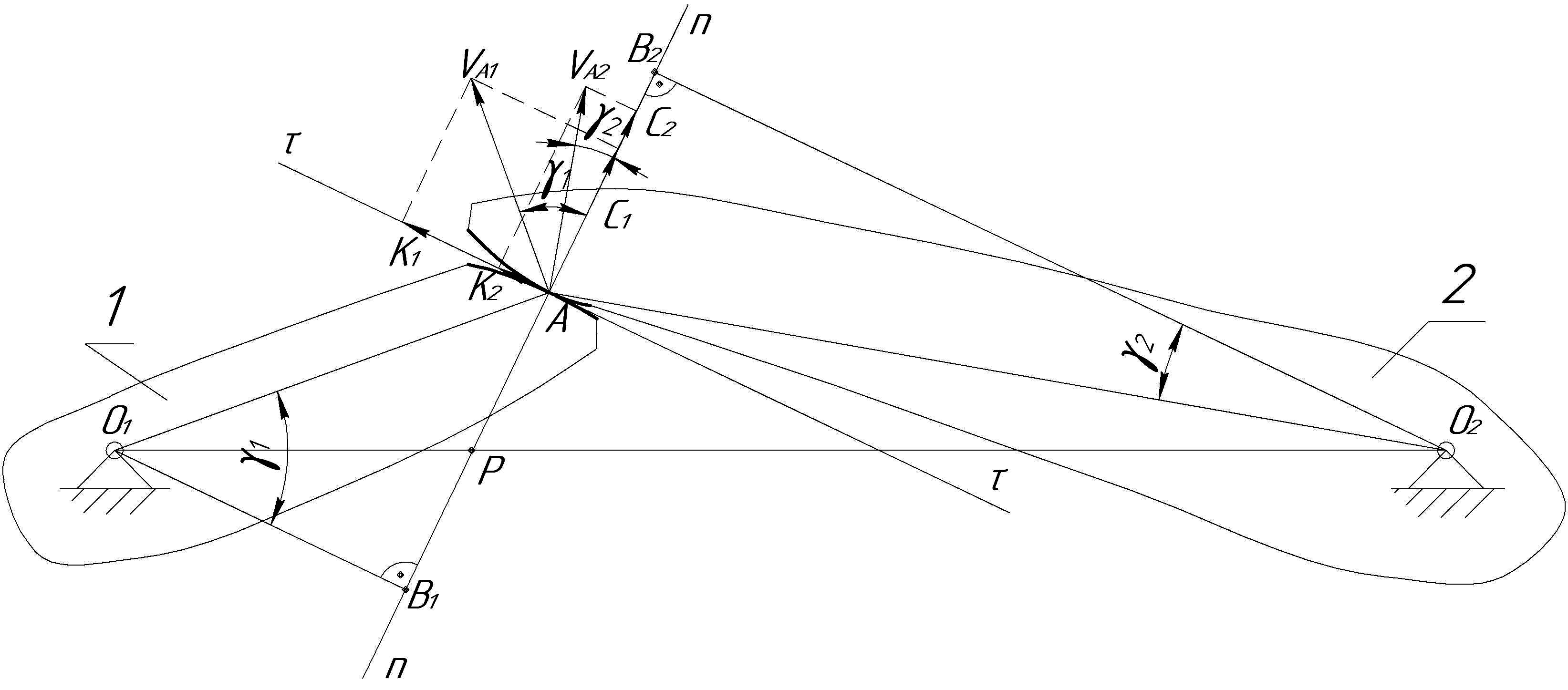
Рисунок 8.1 - К основной теореме плоского зацепления

3. Таким образом, остается единственный правильный вариант

С₁ = С₂

Изобразим отдельно кинематическую пару 1-2 с соблюдением этого условия (рисунок 8.2.). Запишем условие С₁ = С₂ через абсолютные скорости точек профилей:

В полученное равенство подставим значения и по уравнениям (8.1.):

(8.2.)

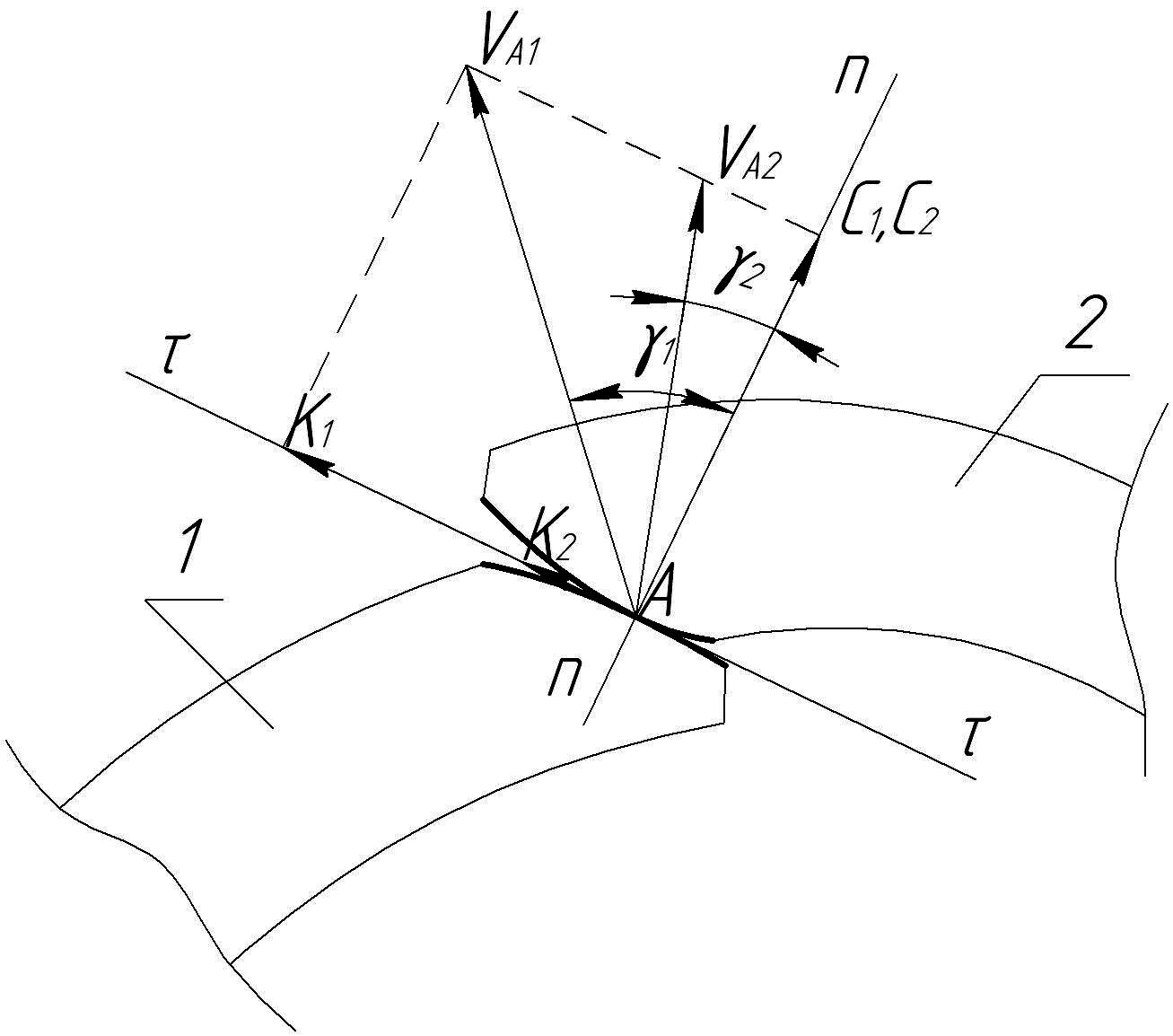
Рисунок 8.2 - Условие равенства проекций скоростей С₁ = С₂

Заметим, что  АО₁В₁= ₁, так как вектор перпендикулярен О₁А₁, а О₁В₁ –перпендикуляр к общей нормали. Аналогично  АО₂В₂ = ₂. Из треугольников АО₁В₁ и АО₂В₂ получим

(О₁А)cos₁= O₁B₁,

(O₂A)cos₂ = O₂B₂.

Тогда из (8.2.) получаем:

B₂ (8.3.)

Рассмотрим треугольники О₁В₁Р и О₂В₂Р. Они подобны по равенству углов. В подобных треугольниках стороны пропорциональны, поэтому

(8.4.)

Из формулы (8.3.) определим передаточное отношение и с учетом (8.4.) получаем:

Запишем формулу передаточного отношения в окончательном виде

(8.5.)

Рассмотрим полученное равенство. Его левая часть характеризует кинематику зацепления – передаточное отношение. Правая часть характеризует геометрию контактирующих поверхностей (профилей), так как положение общей нормали целиком и полностью зависит от геометрии профилей. Таким образом, получена аналитическая зависимость между геометрией контактирующих профилей и их кинематикой. Это и есть основная теорема зацепления.

Если зацепление правильное, то есть контакт между профилями не нарушается, то общая нормаль к профилям, проведенная через точку их контакта, делит межосевое расстояние на отрезки, обратно пропорциональные угловым скоростям звеньев.

Следствия из основной теоремы зацепления.

Для постоянства передаточного отношения , необходимо, чтобы отношение отрезков было постоянным, а это возможно при неизменном межосевом расстоянии О₁О₂, если точка Р занимает на межосевой линии одно и тоже положение. Это теоретически возможно в двух случаях:

а) общие нормали к контактирующим профилям в процессе зацепления образуют пучок прямых, проходящих через одну и ту же точку Р (рисунок 8.3а); этот случай имеет место в циклоидальном зацеплении (применяется в механизмах приборов, часовых механизмах);

б) линия общей нормали занимает неизменное положение, а точка контакта профилей перемещается вдоль нее; это характерно для зацепления эвольвентных профилей. (рисунок 8.3б).

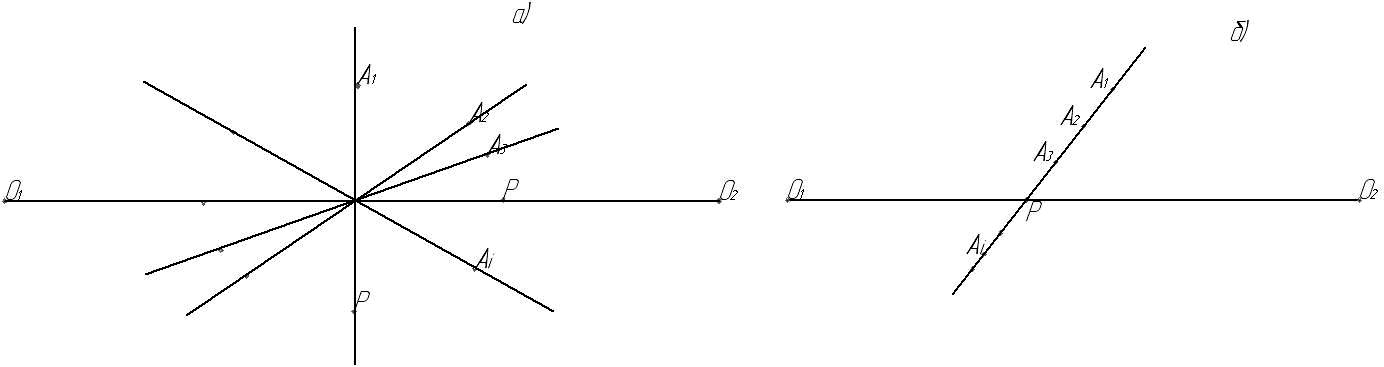
Рисунок 8.3 – Возможны варианты постоянства

1. Проекции скоростей точек контакта звеньев на общую касательную - не равны: К₁ К₂ при С₁= С₂. А это значит, что в процессе зацепления происходит скольжение профилей. Это явление отрицательное, вызывающее износ контактирующих поверхностей звеньев. При проектировании передач проскальзывание профилей стараются уменьшить.