5.6.4 Уравнения движения машины в дифференциальной форме

Дифференциальные уравнения движения машины можно получить путем использования методов приведения сил и масс.

Запишем теорему об изменении кинетической энергии системы материальных тел на бесконечно малом перемещении:

(5.1)

где А - работа всех внешних сил, реально действующих в машине; Т - кинетическая энергия всех звеньев машины.

На бесконечно малом перемещении работа сил бесконечно малая величина и изменение кинетической энергии также бесконечно мало. Разделим обе части уравнения на бесконечно малую величину dt:

, ,

где - мгновенная мощность всех сил, действующих на звенья механизма.

Метод приведения масс и сил позволяет нам выразить N и Т машины через приведенную массу и приведенную силу. Тогда теорема об изменении кинетической энергии запишется в следующем виде:

.

5.6.4.1 Звено приведения движется поступательно

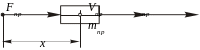
Рассмотрим случай поступательного движущегося звена приведения (материальной точки). В этом случае вся система может быть представлена материальной точкой, движущейся со скоростью V_пр и ускорением а_пр под действием силы F_пр и имеющей массу m_пр (рисунок 5.6). Тогда мощность звена приведения:

, (5.2)

а его кинетическая энергия:

. (5.3)

114ать уравнение движения машины (5.1) может 114ать записано в следующем виде:

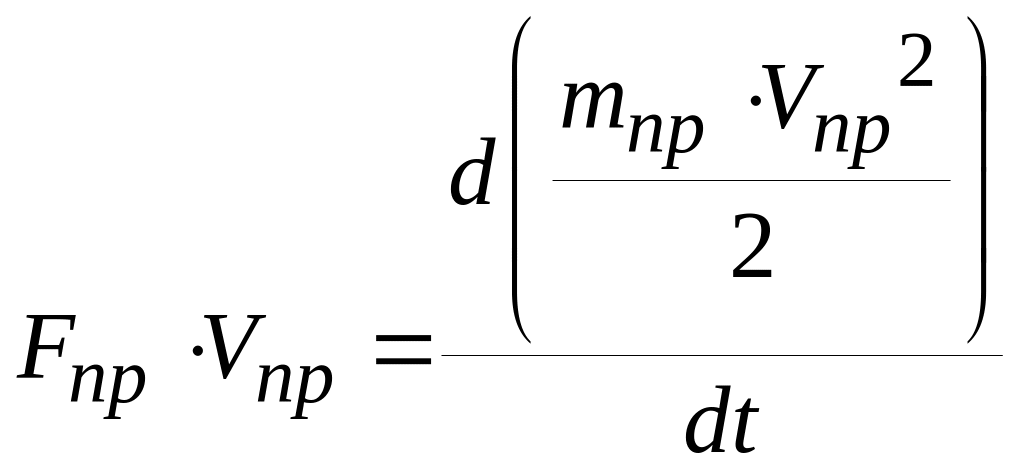. (5.4)

Рисунок 5.6 - Поступательное движение звена приведения

В правой части уравнения мы имеем производную от произведения двух переменных величин m_пр=m(x, V, t) и V_пр=V(x, t). Как правило m_пр=f₁(t), F_пр=f₂(t) и V_пр=f₃(t). Возьмем производную от произведения двух переменных величин m_пр и V_пр по времени t:

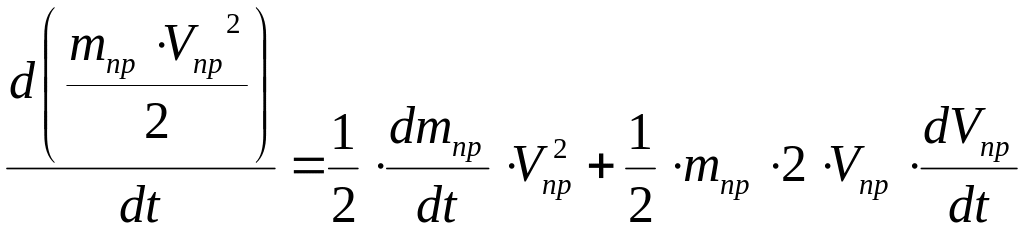, (5.5)

здесь - ускорение материальной точки.

Разделим и умножим первый член правой части полученного равенства на бесконечно малую величину dS_пр - перемещение материальной точки приведения:

,

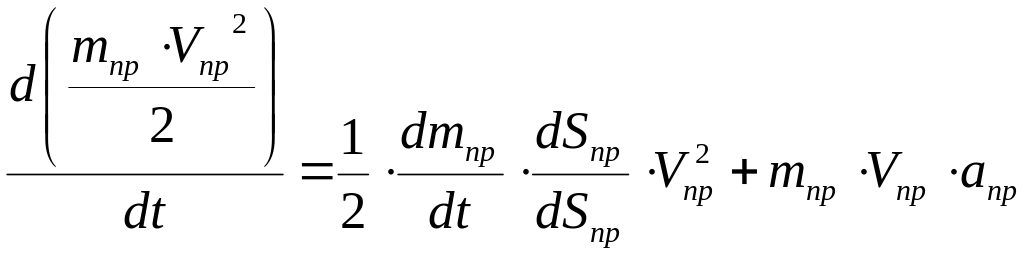здесь - скорость материальной точки приведения.

Подставим полученное выражение в исходное уравнение (5.4):

. (5.6)

Сократим левую и правую части уравнения (5.6) на V_пр:

. (5.7)

Уравнение (5.7)- дифференциальное уравнение движения машины в 115ать115115 виде. Это уравнение применяется в том случае, 115ать115 силы и массы 115ать115115ння115115 к поступательно движущемуся звену или точке механизма.

Если m_пр=const, т.е. 115ать115115ння115 маса точки приведения не зависит от времени или 115ать115115ння механизма, то и 115ать уравнение 115ат принимает вид дифференциального

,

уравнения поступательно движущегося звена.

5.6.4.2 Звено приведения совершает вращательное движение

Рассмотрим случай, 115ать115 звено приведения совершает вращательное движение. Тогда вся система может 115ать представлена в виде звена, вращающегося с угловой скоростью _пр с ускорением _пр под действием момента М_пр и имеющее момент инерции J_пр (рисунок 5.7):

J_пр=J(, , t), М_пр=М(, , t).

Запишем уравнение движения звена приведения:

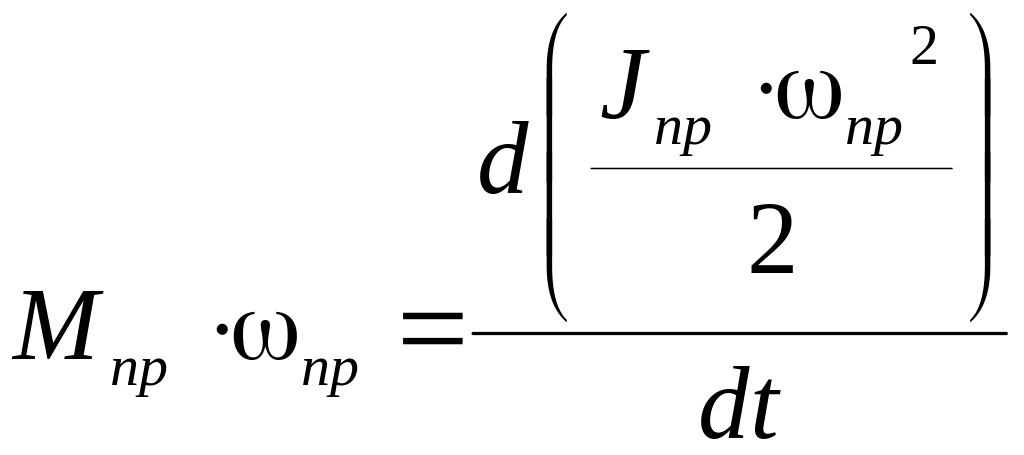. (5.8)

Выполним преобразования, аналогичные тем, которые мы выполним при выводе уравнения (5,7):

,

где - угловое ускорение звена приведения.

,

где _пр – перемещение звена приведения; - угловая скорость звена приведения.

Рисунок 5.7 - Звено приведения совершает вращательное движение

Тогда , откуда получаем:

. (5.9)

Уравнение Мпр - дифференциальное уравнение движения машины в общем виде в случае вращательного движения звена приведения.

Для случая J_пр=const, уравнение Мпр принимает вид М_пр=J_пр_пр - уравнение движения звена приведения совершающего вращательное движение, если все звенья механизма вращающиеся и имеют постоянные массовые характеристики.

Уравнение Fпр более универсально. Уравнение Мпр применяется только в случае, когда звено приведения совершает вращательное движение, а точка может принадлежать звену, совершающему любое движение. На практике чаще используют уравнение Мпр в связи с тем, что силы и массы чаще приводят к валу двигателя - вращающемуся звену. Задача динамики машины чаще сводится к нахождению момента двигателя по заданному закону движения машины и некоторым силам, действующим на звенья машины.

.

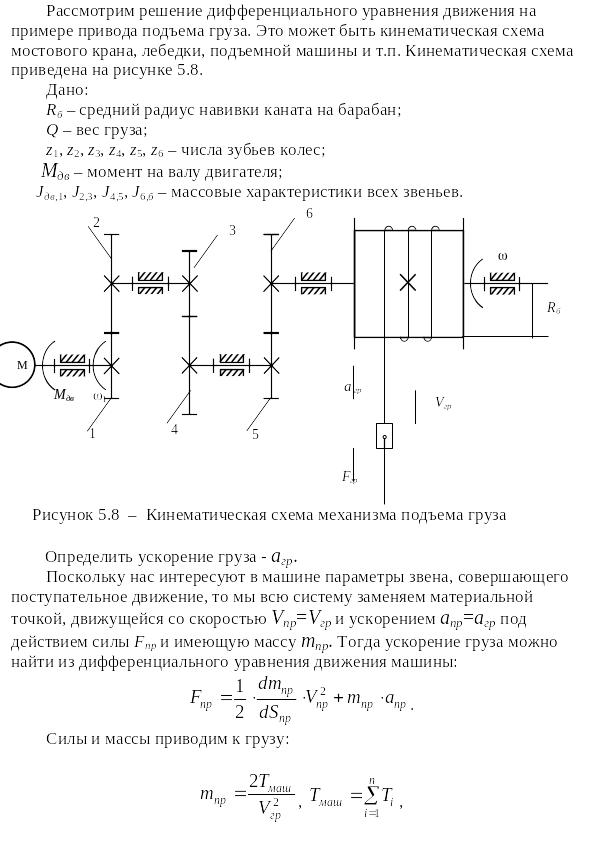
Подставим полученное T_маш в m_пр и сократим на:

.

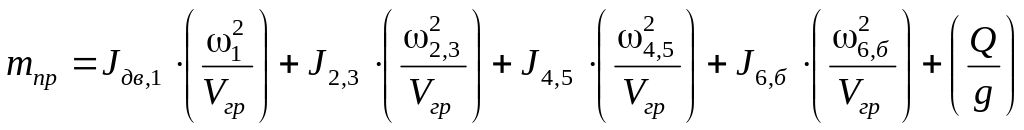Линейную скорость груза выразим через угловую скорость барабана и его радиус:

.

Тогда .

Но ; ;

.

Из анализа уравнения m_пр видно, что все составляющие, входящие в уравнение, постоянны, следовательно, m_пр=const (если пренебречь весом каната), тогда:

, .

Находим величину F_пр из условия равенства мощностей:

, .

Внешние силы - вес груза Q и момент двигателя M_дв. ₁ противоположно ₆. Момент на валу двигателя должен быть направлен в сторону ₁.

Мощность всех сил:

.

Тогда , - берем по модулю, т.к. знак передаточного отношения мы учли при определении мощностей:

.

При различных числовых значениях возможны следующие варианты:

1) F_пр=0, а_пр=0 – равномерное движение груза;

2) F_пр>0, а_пр>0 – ускоренное движение груза;

3) F_пр<0, а_пр<0 – замедленное движение груза.