5.5.2 Определение к.П.Д. Последовательно соединенных механизмов

Изобразим условно i последовательно соединенных механизмов (рисунок 5.4).

Рисунок 5.4 - Последовательное соединение механизмов

Пусть на вход первого механизма поступает работа движущих сил А_дв, тогда на выходе последовательно соединенных механизмов мы должны получить работу, необходимую для преодоления сил полезных сопротивлений А_пс.

Обозначим к.п.д. первого механизма ₁, второго - ₂ и т.д.

Если работа движущих сил, получаемая первым механизмом А_дв, то работа, передаваемая им второму механизму:

.

Второй механизм получает на входе работу А₁ и передает третьему А₂:

.

Работа, отдаваемая i-м механизмом:

.

Откуда получаем:

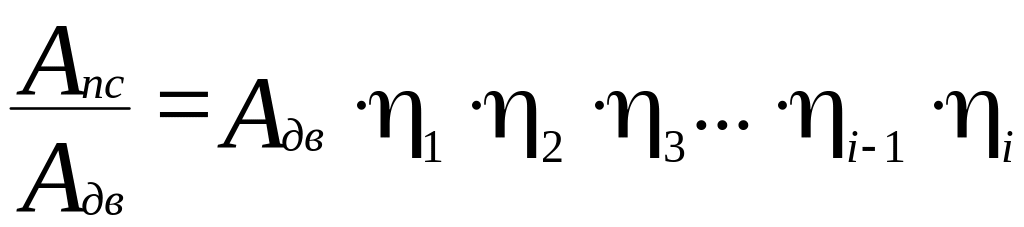или .

Общий к.п.д. при последовательном соединении механизмов равен произведению к.п.д. всех последовательно соединенных механизмов.

Из формулы для определения общего к.п.д. при последовательном соединении механизмов видно, что он меньше наименьшего в системе.

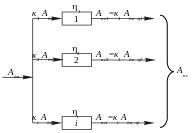
5.5.3 Определение к.П.Д. При параллельном соединении механизмов

Изобразим условно параллельное соединение механизмов (рисунок 5.5). Параллельное соединение механизмов встречается редко. Стараются на каждый механизм ставить индивидуальный двигатель.

При параллельном соединении механизмов с главного вала распределяется работа движущих сил по отдельным механизмам.

При этом необходимо знать, как распределяется работа движущих сил на каждый механизм. Распределение работ (мощностей) характеризуется коэффициентом распределения нагрузки к. Для каждого механизма свой коэффициент к. Сумма коэффициентов равна 1:

.

Работа движущих сил на входе каждого механизма:

; .

Если к.п.д. каждого механизма ₁, ₂, ₃, … _i, то работа сил полезного сопротивления на выходе каждого механизма:

; .

Рисунок 5.5 - Параллельное соединение механизмов

Общая работа сил полезных сопротивлений определяется как сумма работ сил полезных сопротивлений каждого механизма:

или ,

откуда получаем , .

При смешанном соединении механизмов методика определения к.п.д. машины зависит от количества параллельных и последовательных цепей, а также их расположения.

5.6 Уравнения движения машины в дифференциальной форме

5.6.1 Общие сведения

В практике проектирования и исследования машин приходится решать задачи определения кинематических и динамических параметров сложных систем - машин агрегатов. Представить уравнение движения машины в форме закона изменения кинетической энергии можно для любого машинного агрегата, однако уравнения получаются сложными и громоздкими. Для упрощения решения задачи динамики машинного агрегата пользуются методом приведения сил и масс, позволяющим свести решение задачи динамики машины, содержащей множество звеньев, к задаче динамики одного звена, параметры которого в машине нас интересуют. Для этого к этому звену или материальной точке (если звено совершает поступательное движение) приводят массы всех звеньев и все внешние активные силы и пары сил, действующие в машине.

Звено, к которому приводятся все массы и силы, называется звеном приведения.

При этом динамические и кинематические параметры звена приведения под действием приведенных сил и приведенных масс остаются такими же, как и при действии реальных масс и реальных сил, действующих в машине.

Если в машине нас интересуют параметры поступательно движущегося звена (материальной точки), то данное звено считают звеном приведения и к нему приводят все массы и силы. Задача динамики машины в этом случае сводится к решению задачи динамики материальной точки, обладающей приведенной массой m_пр движущейся со скоростью V_пр и ускорением а_пр под действием приведенной силы F_пр.

Если в машине нас интересуют параметры звена, совершающего вращательное движение, то данное звено считают звеном приведения и к нему приводят все массы и силы. Задача динамики машины в этом случае сводится к решению задачи динамики вращающегося звена, обладающего массовой характеристикой - приведенным моментом инерции - J_пр и движущегося со скоростью _пр и ускорением _пр под действием приведенного момента М_пр.