4.2 Трение в низших кинематических парах

4.2.1 Трение в поступательной кинематической паре

Рассмотрим, как может быть учтено трение в низших кинематических парах для некоторых случаев, с которыми приходится наиболее часто встречаться в машинах.

Рассмотрим трение на наклонной плоскости. Найдем силу , необходимую для равномерного перемещения груза весом вверх по наклонной плоскости, если коэффициент трения скольжения равен . Наклонная плоскость и сила составляют с горизонтом углы, соответственно равные и .

Рисунок 4.1 – Силы, действующие на тело на наклонной плоскости

При движении тела на него действуют силы , , нормальная реакция плоскости и сила трения .

Заменим силы и равнодействующей , которая составит с направлением, перпендикулярным плоскости, угол трения .

Построим для сил , и замкнутый треугольник. Тогда по теореме синусов получим:

, (4.5)

откуда находим, что

. (4.6)

При отсутствии трения последнее равенство (4.6) примет вид

. (4.7)

Из определения известно, что к. п. д. наклонной плоскости равен отношению работ сил и на пути , т. е.

.

При горизонтальном направлении силы угол и

; .

В этом случае

. (4.8)

Если же груз будет опускаться по наклонной плоскости под влиянием веса , то сила трения в этом случае будет направлена уже вверх, а горизонтальная сила , поддерживающая равномерный спуск груза, определится из треугольника сил:

.

В случае по формуле находим:

. (4.9)

Отсюда следует, что если угол равен или меньше , то к. п. д. наклонной плоскости .

В этих случаях даже при отсутствии силы груз опускаться не будет. Такое явление называется самоторможением.

Если , то при отсутствии силы линия действия силы тяжести пройдет вне конуса трения и движение груза будет равноускоренное.

Для определения угла , при котором к. п. д. достигает максимума, возьмем производную от по и приравняем ее нулю. Пользуясь равенством (4.9), получим:

, (4.10)

откуда

,

или

. (4.11)

Решив последнее уравнение (4.11) относительно , найдем:

,

откуда

. (4.12)

Подставляя полученное значение в выражение (4.9), получаем:

. (4.13)

Пусть ползун, имеющий форму клина (клинчатый ползун) и нагруженный вертикальной силой , движется равномерно в желобе под действием горизонтальной силы , равной силе трения . В этом случае должно быть выполнено равенство

.

Построив для ползуна треугольник сил, получим , где угол, который составляет каждая грань клина с вертикальной плоскостью.

Зная, что , находим силу трения:

,

где

. (4.14)

Из равенства (4.14) следует, что приведенный коэффициент трения клинчатого ползуна больше коэффициента трения плоского ползуна.

Рассмотрим трение в цилиндрическом ползуне. Если ползун цилиндрический, то для определения силы трения примем гипотезу о равномерной вертикальной осадке каждой образующей цилиндра. Проведем нормаль под углом к вертикали и обозначим через осадку по направлению этой нормали, тогда радиальная осадка .

Обозначим через и удельные давления на поверхности направляющей в нижних точках и в точках, расположенных в нормальной плоскости, проведенной под углом .

Так как удельные давления пропорциональны перемещениям в вертикальной плоскости, то

, или .

Выделим на поверхности направляющей элементарную полоску шириной и длиной , равной длине ползуна, тогда элементарная сила трения, приходящаяся на эту полоску,

, (4.15)

Сила трения, приходящаяся на всю трущуюся поверхность,

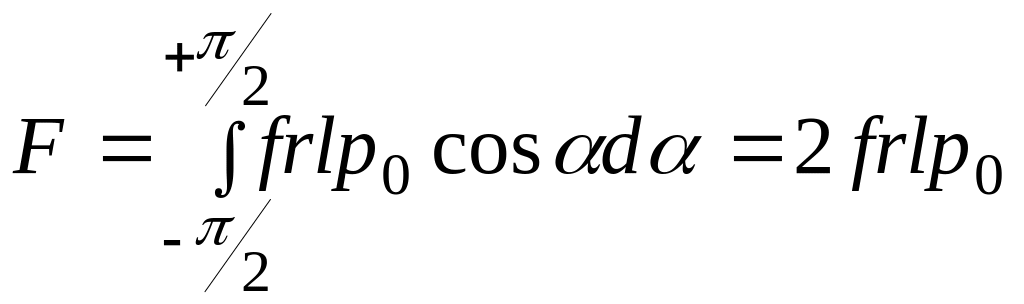. (4.16)

Проектируя все силы, действующие на ползун, на вертикальную ось, получим:

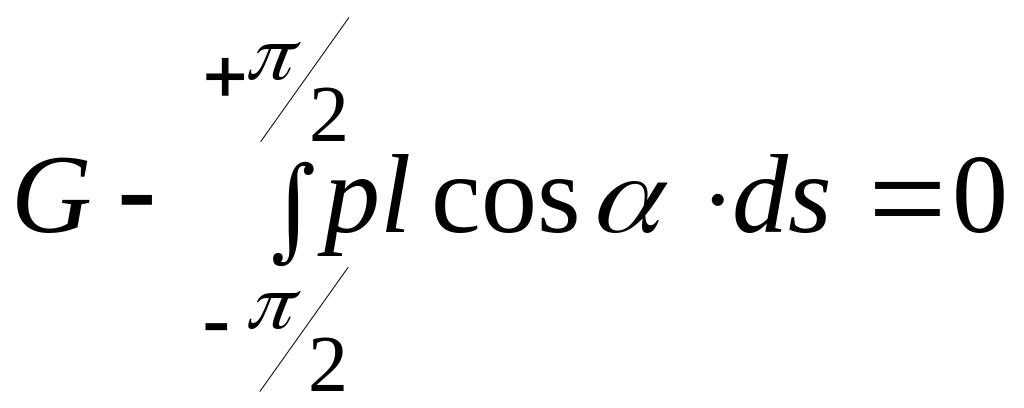(4.17)

или

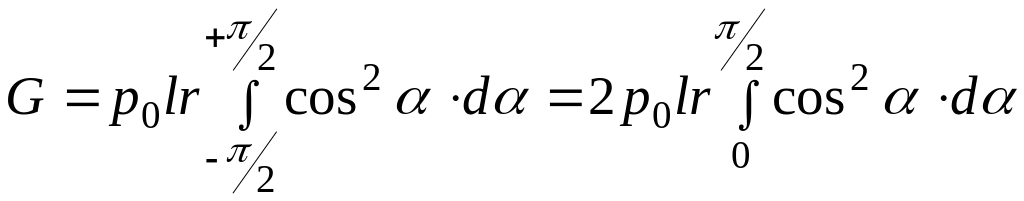. (4.18)

Вычислим интеграл:

,

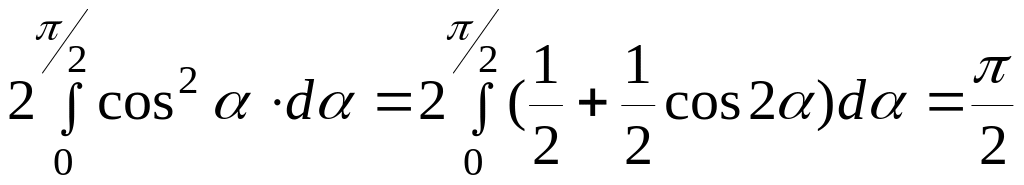откуда

, или .

Подставив найденное значение в выражение силы трения , найдем:

,

или окончательно

, (4.19)

где приведенный коэффициент трения .