3.3 Условие статической определимости кинематической цепи

Силовой расчет механизма, осуществляемый с учетом сил инерции его звеньев, называется кинетостатическим.

Каждая реакция в кинематической паре определяется тремя скалярными параметрами: точкой приложения, величиной, положением линии действия. Т.е. каждая неизвестная или неполностью известная реакция вносит в скалярное уравнение от одной до трех неизвестных скалярных величин.

В первом приближении будем вести расчет без учета сил трения в кинематических парах, т.е. поверхности контакта звеньев будем считать идеальными. В таком случае линии действия реакций в парах будут направлены по нормалям к их элементам.

В одноподвижной вращательной паре линия действия реакции, например, R_m,p пересекает ось шарнира, т.е. точкой приложения ее можно считать центр шарнира; величина и направление этой реакции неизвестны, что эквивалентно двум скалярным неизвестным величинам. Для отыскания такой реакции представим ее в виде нормальной и тангенциальной составляющих.

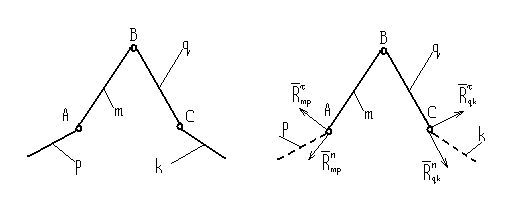
Рисунок 3.3 – Реакция во вращательной кинематической паре

Линии действия этих составляющих располагаем вдоль соединяющего центры шарниров А и В отрезка АВ ( ) и перпендикулярно ему ( ).

Аналогично разложена на две составляющие реакция .

В одноподвижной поступательной паре реакция направлена перпендикулярно направляющей, но неизвестны ее величина и точка приложения, что эквивалентно двум скалярным неизвестным величинам.

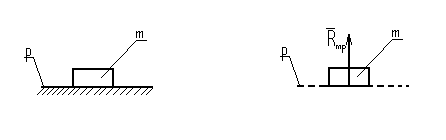
Рисунок 3.4 – Реакция в поступательной кинематической паре

В двухподвижной высшей паре реакция приложена в точке контакта звеньев, ее линия действия направлена по общей нормали к поверхностям в точке их контакта, и только величина ее неизвестна, что соответствует только одной скалярной неизвестной величине.

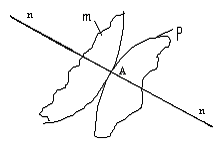
Рисунок 3.5 – Реакция в высшей кинематической паре

Таким образом, для кинематической цепи из п звеньев, содержащей Р₁ одноподвижных пар и Р₂ двухподвижных, справедливо следующее.

Общее количество скалярных неизвестных параметров реакций во всех парах цепи после замены высших двухподвижных пар низшими одноподвижными составляет 2Р₁.

Для каждого звена можно составить 3 скалярных уравнения равновесия, всего 3п.

Т.е. рассматриваемая цепь будет статически определимой, если 3п=2Р_1, т.е. .

Последнее уравнение характеризует структурную группу Ассура. Следовательно, разделяя механизм на части с целью сделать реакции в парах внешними силами и тем самым ввести их в уравнения для их отыскания, нужно в качестве таких частей брать группы Ассура.

3.4 Силовое исследование механизма по методу академика н.Г.Бруевича.

Этот вопрос будет рассмотрен на примере шарнирного четырехзвенника.

Обычно бывают известны:

1. план механизма в исследуемом положении (рис. 3.6);

2. закон движения ведущего звена ( );

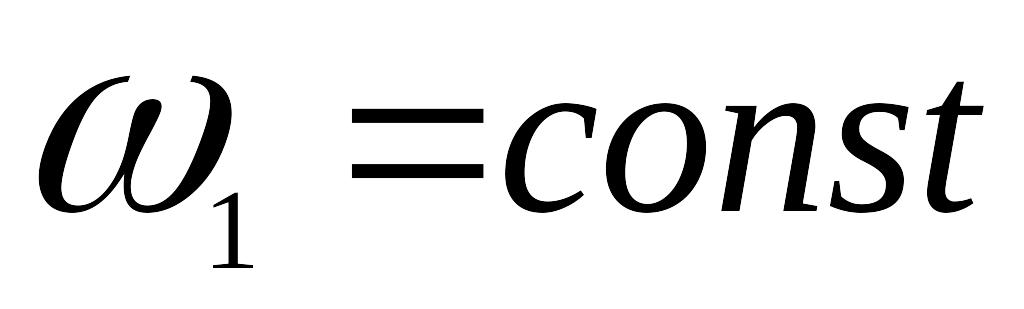3. массы 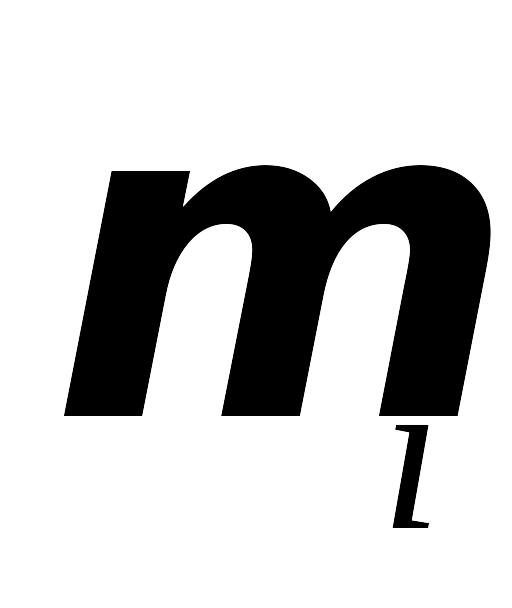и моменты инерции 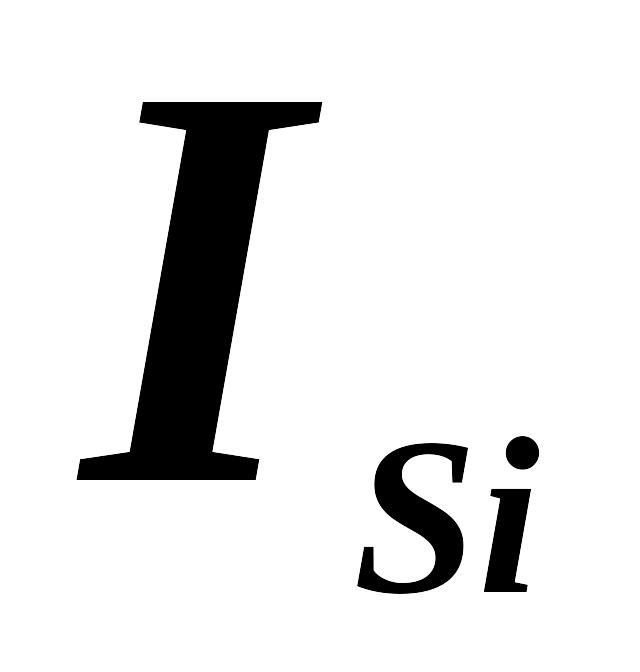звеньев, положения их центров масс;

4. внешние нагрузки, приложенные к звеньям, в том числе силы тяжести звеньев 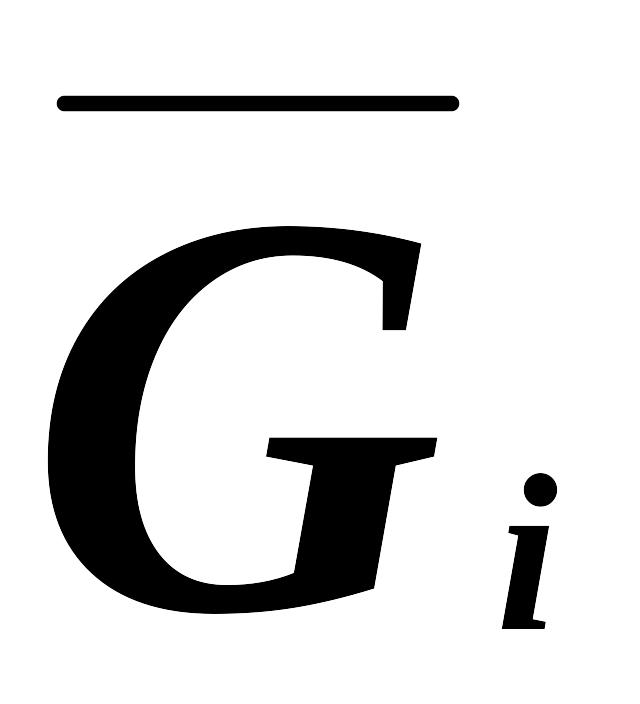, сила полезного сопротивления .

Требуется определить реакции во всех кинематических парах и уравновешивающую нагрузку (уравновешивающую силу и/или уравновешивающий момент сил ), приложенную к звену 1.

Кинетостатический расчет механизма будет осуществлен без учета трения в кинематических парах.

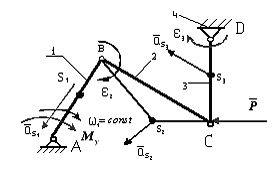
Рисунок 3.6 – План механизма в исследуемом положении

Начать расчет следует с построения планов скоростей и ускорений для исследуемого положения механизма по заданному закону движения ведущего звена 1 (см. раздел 2). С помощью этих планов определяем ускорения центров тяжести и угловые ускорения звеньев. А это позволяет определить главные векторы и главные моменты сил инерции звеньев (см. п. 3.2) для рассмотрения их как находящихся в равновесии с целью определения искомых нагрузок из уравнений статики.

Таким образом, и далее считаем известными.

Рассмотрим группу, состоящую из звеньев 2 и 3 (диада Ассура).

Для этого прежде всего с учетом масштабного коэффициента длины изобразим звенья 2 и 3 с сохранением их положений.

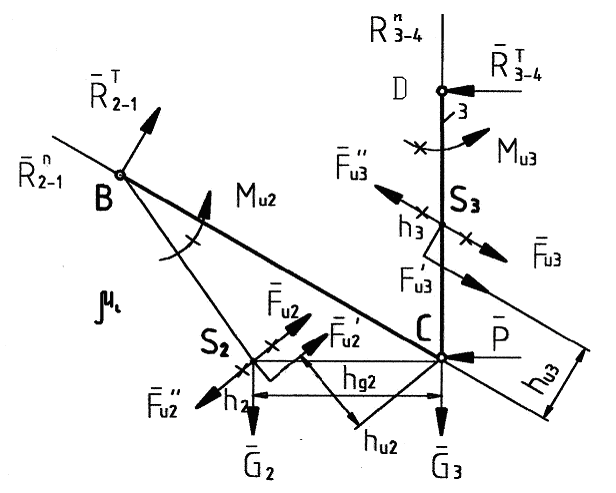
Рисунок 3.7 – План группы 2,3

На плане группы изобразим (не обязательно с соблюдением масштабного коэффициента сил) внешние нагрузки, приложенные к звеньям 2 и 3, и инерционные нагрузки. Моменты сил , заменены парами сил (см. п. 3.2).

Реакции на оставленные в рассмотрении звенья 2 и 3 со стороны мысленно отсоединенных звеньев 1 и 4 ( и ) разложены каждая (см. п. 3.3) на нормальную и тангенциальную составляющие (см. рис. 3.7). Направления тангенциальных составляющих и являются предполагаемыми (они указаны наугад); об определении их истинных направлений см. ниже.

Метод решения задачи не требует предполагать направления нормальных составляющих и , он позволяет сразу найти их истинные направления путем построения замкнутого многоугольника сил, действующих на звенья 2 и 3, и их сил инерции (см. рис. 3.8).

Рассмотрим как находящееся в равновесии звено 2 (без звена 3). В этом случае в уравнениях равновесия звена 2 должна быть учтена реакция , о которой известно лишь то, что ее линия действия проходит через точку С. Уравнение моментов сил, действующих на звено 2, относительно точки С является разрешимым, т.к. единственной скалярной неизвестной величиной в нем является ; силы и в это уравнение не войдут, т.к. их линии действия проходят через точку С, следовательно, их моменты относительно точки С порознь равны нулю.

Здесь и в дальнейшем при составлении уравнений моменты сил, направленные против хода часовой стрелки, будем измерять положительными числами, по ходу – отрицательными.

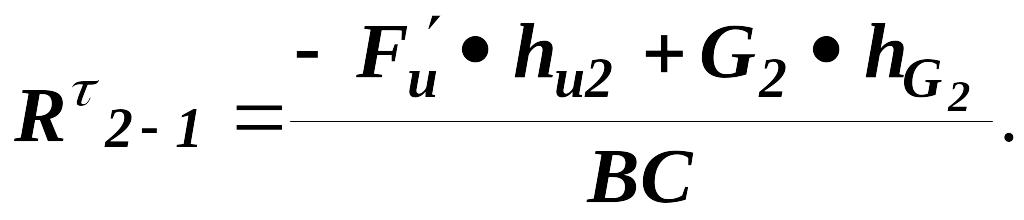(3.3)

Получение решения в виде >0 свидетельствует о том, что предположенное направление является истинным, в противном случае истинное направление противоположно предположенному.

Аналогично рассматриваем равновесие звена 3:

(3.4)

В нашем случае, когда на звенья 2 и 3 действуют нагрузки только в виде сил (моменты сил заменены парами сил), можно в уравнения (3.3) и (3.4) подставлять не величины плеч сил, а длины их чертежных изображений, измеренные, например, в миллиметрах чертежа.

Определяем нормальные составляющие сил реакций в шарнирах В и D: . Для этого рассмотрим равновесие группы звеньев 2,3. Составляем условие равновесия группы: - геометрическая сумма сил, действующих на группу звеньев 2,3 равна нулю. Запишем это условие. Порядок записи может быть произвольным, но для облегчения дальнейшей работы примем его таким: сначала перечисляем все силы, действующие на звено 2, начиная с тангенциальной составляющей силы реакции в шарнире В - , затем перечисляем все силы, действующие на звено 3 заканчивая тангенциальной составляющей силы реакции в шарнире D - .

. (3.5)

Сложение сил выполняем графически, для чего задаёмся масштабным коэффициентом сил . С учётом масштабного коэффициента последовательно складываем силы, перечисленные в уравнении (3.5). При решении уравнения графическим методом определяем и (см. рис. 3.8). С учётом находим их абсолютные значения. Имея нормальные и тангенциальные составляющие сил реакций в шарнирах В и D, находим их полные значения, как векторные суммы:

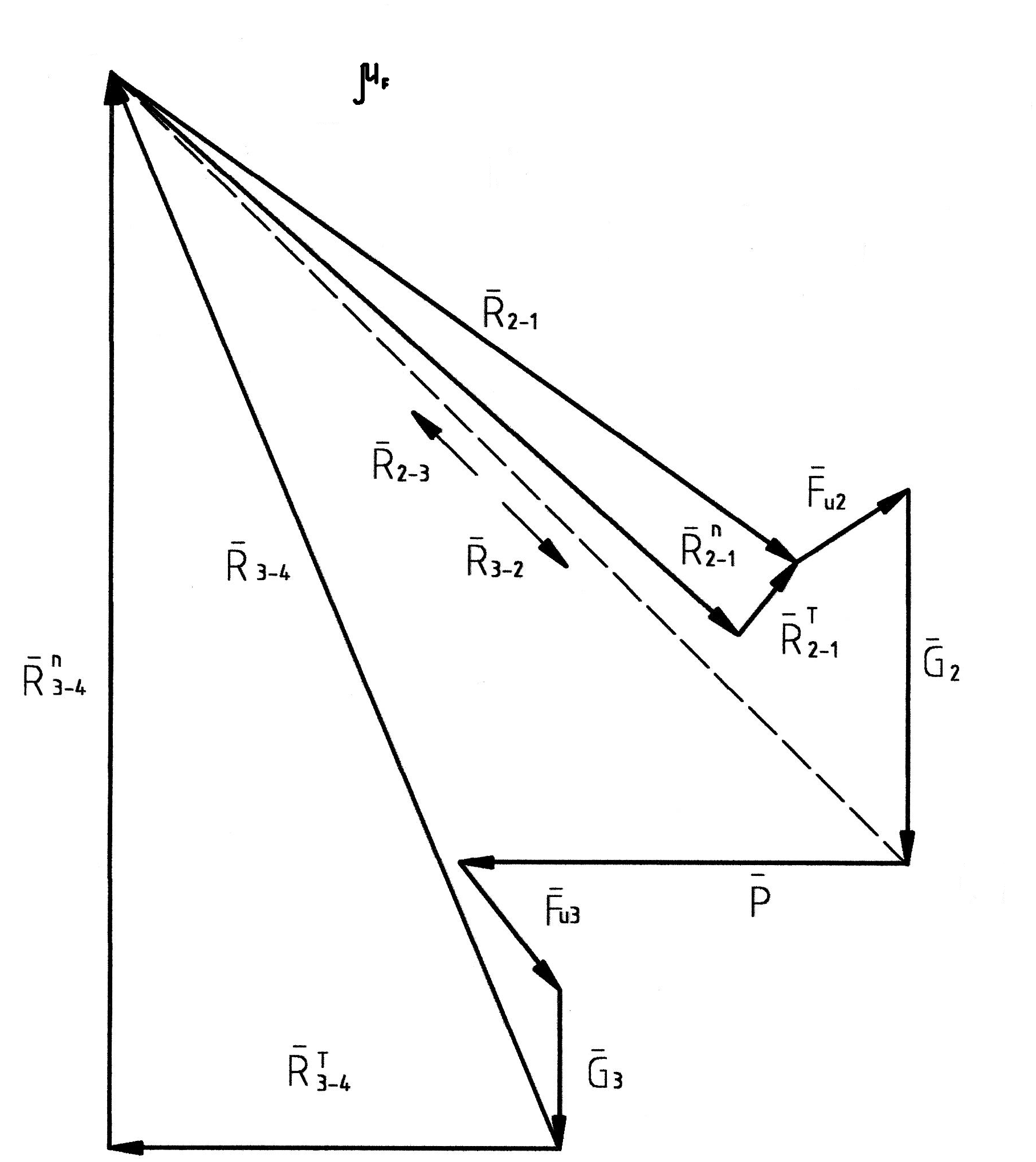
Рисунок 3.8 – Планы сил, действующих на звенья 2 и 3 и их сил инерции

(3.6)

(3.7)

Определяем силу реакции в шарнире С.

Для этого рассматриваем равновесие звена 2. На звено 2 действуют все ранее указанные силы и неизвестная сила реакции в шарнире С, действующая на звено 2 со стороны отсоединённого звена 3.

Составляем уравнение равновесия звена 2, из которого графическим способом определяем :

. (3.8)

В случае, если бы порядок изображения векторов сил уравнения (3.8) был произвольным, было бы необходимо построить еще три дополнительных многоугольника сил для решения уравнений (3.5), (3.6), (3.7). При выбранном же порядке в качестве каждого из этих трех многоугольников сил может быть рассмотрена нужная часть многоугольника сил на рис. 3.8.

Определим теперь - реакцию в шарнире А и приложенный к кривошипу 1 уравновешивающий момент сил . Для этого рассмотрим как находящееся в равновесии звено 1.

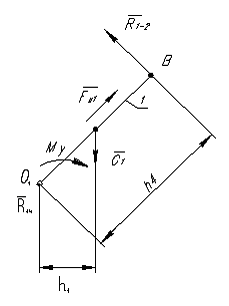
Рисунок 3.9 – Схема нагружения кривошипа

Изобразим кривошип в исследуемом пложении с учетом масштабного коэффициента длины . Покажем на плане звена все действующие на него нагрузки и инерционные (см. рис. 3.9).

- сила тяжести звена.

так как .

.

Для определения Му составляем уравнение моментов относительно точки А

,

.

Из полученного уравнения определяем Му – уравновешивающий момент:

.

Для определения силы реакции составляем уравнение равновесия кривошипа.

.

С учётом масштабного коэффициента строим план сил, действующих на первое звено (рис.3.10) . Решение уравнения геометрической суммы сил даёт определение полной реакции в шарнире A.

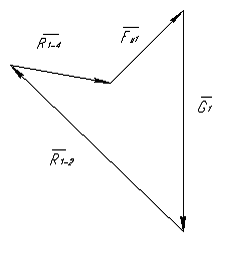
Рисунок 3.10 – План сил, действующих на звено 1 и его сил инерции