
- •1 Структура механизмов
- •2 Кинематическое исследование плоских стержневых механизмов
- •3 Силовой анализ механизмов
- •4 Трение в механизмах и машинах
- •5 Динамическое исследование машин и механизмов
- •Общие сведения 109
- •6 Уравновешивание механизмов
- •9 Кулачковые механизмы. Анализ и синтез
- •Введение
- •Раздел 1 «Структура механизмов» посвящен структурному анализу и принципам образования механизмов, их классификации.
- •1 Структура механизмов
- •1.1 Основные понятия
- •1.2 Кинематические пары и их классификация
- •1.3 Кинематические цепи
- •1.4 Определение степени подвижности
- •1.5 Пассивные связи и избыточные звенья
- •1.6 Классификация механизмов
- •1.6.1 Механизмы с низшими кинематическими парами
- •1.6.2 Механизмы с высшими кинематическими парами
- •1.6.3 Условия рационального исполнения основных видов механизмов
- •Шарнирный четырехзвенник
- •2 Кинематическое исследование плоских стержневых механизмов
- •2.1 Методы кинематического исследования
- •2.2 Кинематические характеристики точки и звена
- •2.3 Метод планов
- •2.3.1 Планы механизмов
- •2.3.2 Планы скоростей
- •2.3.3 Определение угловых скоростей звеньев
- •2.3.4 Планы ускорений
- •2.3.5 Определение угловых ускорений звеньев
- •2.3.6 Свойства планов скоростей и ускорений
- •2.3.7 Построение планов скоростей и ускорений кулисного механизма
- •2.4 Определение коэффициента изменения скорости хода
- •3 Силовой анализ механизмов
- •3.1 Общие положения
- •3.2 Силы инерции звеньев плоского механизма
- •3.3 Условие статической определимости кинематической цепи
- •3.4 Силовое исследование механизма по методу академика н.Г.Бруевича.
- •3.5 Способ профессора н.Е.Жуковского
- •4 Трение в механизмах и машинах
- •4.1 Основные определения
- •4.2 Трение в низших кинематических парах
- •4.2.1 Трение в поступательной кинематической паре
- •4.2.2 Трение во вращательной кинематической паре при наличии зазора между шипом и подшипником
- •4.2.3 Трение в винтовой кинематической паре
- •4.3 Трение качения
- •5 Динамическое исследование машин и механизмов
- •5.1 Задачи динамического исследования машин
- •5.2 Классификация сил, действующих в машине
- •5.3 Уравнения движения машины
- •5.4 Режимы работы машины
- •5.4.1 Режим пуска
- •5.4.2 Режим установившегося движения
- •5.4.2.1 Равновесный режим установившегося движения
- •5.4.2.2 Неравновесный режим установившегося движения
- •5.4.3 Режим выбега машины
- •5.5 Коэффициент полезного действия машины
- •5.5.1 Общие сведения
- •5.5.2 Определение к.П.Д. Последовательно соединенных механизмов
- •5.5.3 Определение к.П.Д. При параллельном соединении механизмов
- •5.6 Уравнения движения машины в дифференциальной форме
- •5.6.1 Общие сведения
- •5.6.2 Метод приведения масс
- •5.6.3 Метод приведения сил
- •5.6.4 Уравнения движения машины в дифференциальной форме
- •5.6.4.1 Звено приведения движется поступательно
- •5.6.4.2 Звено приведения совершает вращательное движение
- •6 Уравновешивание механизмов
- •6.1 Регулирование хода машин
- •6.2 Выбор момента инерции маховика
- •7 Механизмы передачи вращательного движения
- •8. Основы теории плоского эвольвенного зацепления
- •8.1. Основная теорема плоского зацепления
- •8.2 Эвольвента и её свойства
- •Основные свойства эвольвенты
- •Свойства эвольвентного зацепления
- •Эвольвентное реечное зацепление. Исходный контур
- •8.5. Методы нарезания эвольвентных зубьев
- •8.6 Параметры эвольвентного колеса, нарезанного
- •Минимальный радиус кривизны эвольвенты.
- •Или окончательно (8.24)
- •Толщина зуба эвольвентного колеса по дуге любой окружности
- •Из прямоугольного треугольника adPc определяем
- •Виды зацеплений. Плотное зацепление.
- •Определение радиусов начальных окружностей, межосевого расстояния и высоты зуба
- •9 Кулачковые механизмы. Анализ и синтез
- •9.1 Назначение и основные виды
- •9.2 Основные параметры кулачковых механизмов
- •9.2.1 Теоретический и практический профили кулачка
- •9.2.2 Цикл работы кулачкового механизма с вращающимся кулачком
- •9.2.3 Угол давления и угол передачи движения в кулачковом механизме
- •9.3.1.2 Определение закона движения толкателя кулачкового механизма с вращающимся кулачком и поступательно движущимся толкателем
- •9.4 Определение минимального радиуса теоретического профиля кулачка. (Динамический синтез)
- •9.5 Построение центрового и действительного профилей кулачка
- •Перечень ссылок
Шарнирный четырехзвенник
Условия существования кривошипа в шарнирном четырехзвеннике впервые были сформулированы Грасгофом (1826 – 1893) в следующем виде: « Шарнирная четырехзвенная цепь может только тогда образовывать кривошипно – коромысловый или двухкривошипный механизм, когда сумма длин наибольшего и наименьшего звеньев меньше суммы длин двух других звеньев». При закреплении наименьшего звена механизм будет двухкривошипным, а при закреплении одного из соседних с ним звеньев –кривошипно-коромысловым ( причем наименьшее звено будет кривошипом). Во всех иных случаях из цепи получаются двухкоромысловые механизмы. Для доказательства этих условий рассмотрим кривошипно – коромысловый механизм в трех особых положениях ( рис. 1.33).
В первом положении (рис. 1.26.а) из условия, что в треугольнике длина каждой стороны меньше суммы длин двух других сторон, имеем:
а + d < b + c. (1.5)
Таблица 1.3 – Плоские стержневые механизмы
Название механизма |
Условные обозначения (кинематическая схема) |
Назва ланок |
1 |
2 |
3 |
1
2
3
4
A
B
C
D
|
|
1 – кривошип, 2 – шатун, 3 – коромысло 4 – стойка |
1
2
3
4
A
B
C
B
|
|
1 – кривошип, 2 – шатун, 3 – ползун, 4 – стойка |
1
2
3
4
A
C
|
|
1 – кривошип, 2 – кулиса, 3 – кулисный камень, 4 – стойка |
|
|
1 – кривошип, 2 – кулиса, 3 – кулисный камень, 4 – стойка |
|
|
1 – кулиса, 2 – ползун, 3 – кулисный камень, 4 – стойка |

а) б) в)
Рисунок 1.26 - Кривошипно-коромысловый механизм в особых положениях
Аналогично, для второго положения (рис. 1.26.б):
a + b < c + d. (1.6)
Для третьего положения (рис. 1.26.в):
c < b + d – a или a + c < b + d. (1.7)
Складывая неравенства (1.5) и (6), получаем:
2a + b + d < 2c + b + d , т.е. a < c .
Складывая неравенства (1.5) и (1.7), получаем:
2a + c + d < 2b + c + d , т.е. a < b . (1.7)
Складывая неравенства (1.6) и (1.7), получаем:
2a + b + c < 2d + b + c , т.е. a < d . 1.7
Следовательно, кривошип а есть наименьшее звено. Кроме того, все необходимые неравенства (1), (2) и (3) удовлетворяются, если сумма длин наименьшего а и наибольшего b, или с, или d звеньев меньше суммы длин двух других звеньев.
В кривошипно – коромысловом механизме углы между стойкой и кривошипом, а также между шатуном и кривошипом изменяются от 0 до 360°. Следовательно, если в кривошипно – коромысловом механизме сделать стойкой звено а, то получится двухкривошипный механизм с кривошипами b и d. Во всех остальных случаях кривошипа нет, т.е. механизм будет двухкоромысловым.
.


















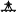



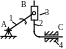 4.
Синусный
4.
Синусный 5.
Тангенсный
5.
Тангенсный