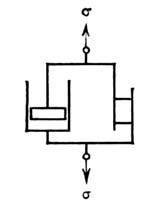
4. Модель реального тела. Модель Бингама(*) – вязкопластическое тело

При последовательном соединении элементов

Р₁=Р₂=Р₃=Р_н

γ₁= γ₁+ γ₂ +γ₃

= ₁+ ₂ +₃

При параллельном соединении элементов

Р=Р₁+Р₂+Р₃ +Р_н

γ₁= γ₁= γ₂ =γ₃

= ₁= ₂ =₃

.

Рис. 4.10. Модель Бингама: параллельное соединение жидкостного элемента(поршень в цилиндре) и тела Сен-Венана

γ

Р_тР Р_тР

Рис.4.11. Реологические кривые модели Бингама

Закон Бингама: Р = Р_т + , (4.7)

причем Р включает две составляющие: разрушающее структуру и вызывающее течение.

По физическому смыслу  и  отличаются, т.к.

=  + Р_{т /} =,(4.8)

ньютоновская вязкость учитывает все сопротивления течению, а пластическая не учитывает прочность структуры, но отражает скорость разрушения, в основном вязкостью дисперсионной среды, которая может меняться в широких пределах. Например, для газов вязкость равна примерно 10^-5 Па с , для стекол и твердых тел – 10¹⁵ - 10²⁰ Па с и более.

Течение такой системы начинается лишь тогда, когда напряжение сдвига превысит какое-то определенное критическое значение P_Т, необходимое для разрушения структуры. Такое течение Бингам назвал пластическим, а напряжение сдвига P_Т - пределом текучести. С точки зрения реологии такие системы называют пластично - вязкими, и закономерности их течения описываются уравнением Бингама.

При отсутствии структурной сетки значение P_Т = 0 и уравнение Бингама переходит в уравнение Ньютона, а пластическая вязкость - в истинную вязкость ньютоновской жидкости. Графическое изображение уравнения Бингама представлено на рис.4.11.

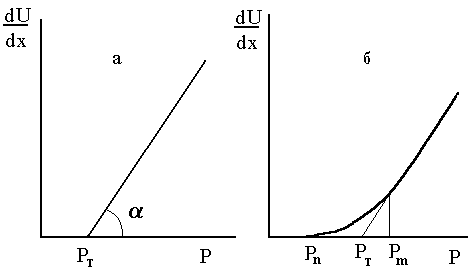
Рис.4.12. Кривая течения бингамовской (а) и реальной пластично-вязкой системы (б).

Согласно рис.4.12, при нагрузках, превышающих Р_т, происходит скачкообразное разрушение структуры, и пластическая вязкость принимает постоянное значение:

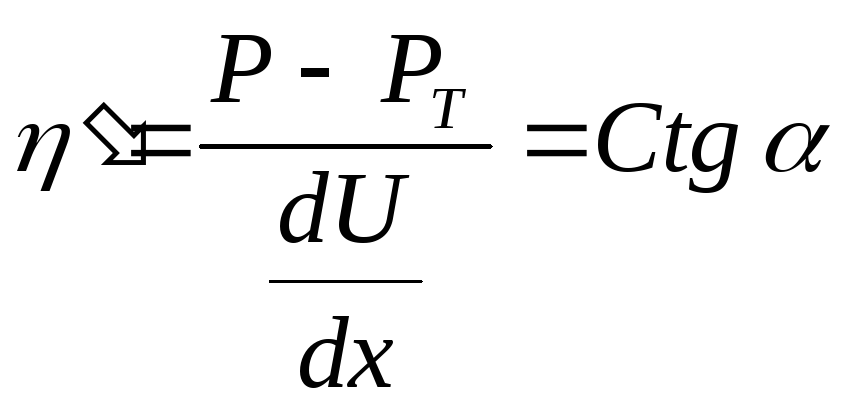(4.9)

Примером систем, хорошо подчиняющихся уравнению Бингама, могут служить пасты из глины и консистентные смазки. Однако для большинства структурированных систем зависимость dU/dx от P выражается не прямой, а кривой (рис.4.12.б). Причина этого явления заключается в том, что при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения Р и dU/dx.

На кривой можно выделить три критических напряжения сдвига:

1) P_n - минимальный предел текучести, соответствующий началу течения; 2) P_т - предел текучeсти по Бингаму, отвечающий отрезку на оси абсцисс, отсекаемому продолжением прямолинейного участка кривой;

3) P_m - максимальное напряжение сдвига, соответствующее значению P, при котором кривая переходит в прямую линию.

В области кривой (P_n - P_m) вязкость не является постоянной величиной и по мере увеличения P уменьшается. При P > P_m структура жидкости разрушается полностью и вязкость принимает постоянное наименьшее для данной системы значение.

Лекция 9. .4.3. Реологические свойства реальных тел

1. Классификация тел по их реологическим свойствам

Все реальные тела по течению делят на:

Жидкообразные (Р_т = 0) и

Твердообразные (Р_т > 0)

В свою очередь жидкообразные тела можно разделить на:

Ньютоновские	Неньютоновские:
	стационарные: 1.псевдопластические 2.дилатантные	нестационарные: (структурированные, характерны явления тиксотропии, реопексии)

Экспериментальные исследования показали, что можно течение жидкообразных систем представить в виде общей зависимости. Это уравнение известно, как математическая модель Оствальда-Вейля^(**):

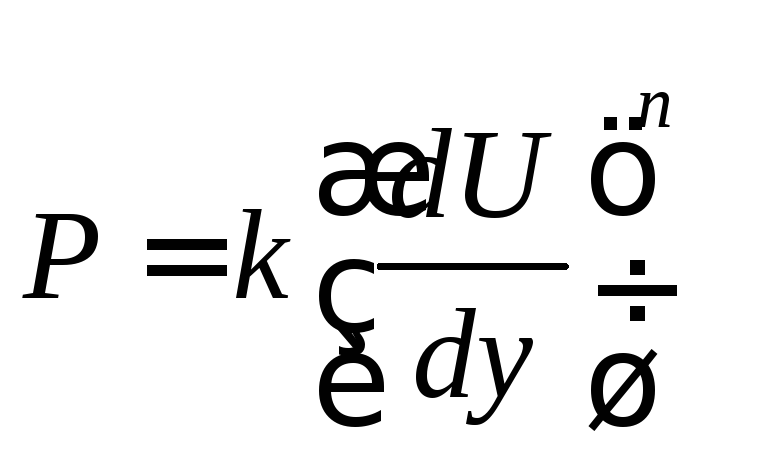. (4.10)

где k и n - постоянные, характеризующие данную жидкообразную систему:

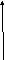
3

1

2

р

η 2

1

3

р

Рис.4.13. Типичные реологические кривые жидкообразных тел.

1. - n=1, ньютоновская системаи константа k совпадает с ньютоновской вязкостью .

2 - n<1, псевдопластические жидкообразные системы

3 - n>1, дилатантные жидкообразные системы

Таким образом, отклонение nот единицы характеризует степень отклонения свойств неньютоновских жидкостей от свойств ньютоновских жидкостей (рис.4.13).

При n< 1 вязкость уменьшается с увеличением скорости сдвига и напряжения. Такие жидкости называютсяпсевдопластическими.

При n > 1 вязкость жидкостей растет с увеличением скорости сдвига и напряжения. Такие жидкости называют дилатантными.

1. - к ньютоновским относятся все чистые жидкости, а также разбавленные коллоидные системы с симметричной формой частиц – суспензии, эмульсии, золи.

2. – к псевдопластическим жидкообразным системам можно отнести разбавленные суспензии с ассиметрической формой частиц, растворы полимеров

Дело в том, что длинные макромолекулы и асимметричные частицы оказывают различное сопротивление потоку в зависимости от их ориентации в потоке. С возрастанием напряжения сдвига и скорости течения жидкости частицы постепенно ориентируются своими большими осями вдоль направления потока. Их хаотическое движение меняется на упорядоченное, что и ведет к уменьшению вязкости.

Если частицы дисперсной фазы анизометричны (эллипсоиды, палочки, пластинки) или способны к деформациям (капельки, макромолекулы), то при течении дисперсионной среды могут проявляться в зависимости от природы и размеров частиц различные тенденции.

Р

Покой поток

Сдвиговые напряжения наряду с приданием частицам вращения стремятся деформировать частицы и определенным образом ориентировать в потоке.

Степень ориентации частиц существенно зависит от скорости деформации, т.е. при малых скоростях течения частицы могут быть полностью разориентированы в потоке, при высоких – ориентированы. Это приводит к изменению вязкости в зависимости о т напряжении я сдвига.

Таким образом, с увеличением напряжения сдвига в псевдопластических системах хаотическое движение частиц упорядочивается и вязкость уменьшается.

В этом случае недостаточно понятия вязкости ньютоновской, используется понятие об эффективной вязкости η_эф = τ/.

3. - Дилатантные или растекающиеся системы. В растекающемся потоке объем системы уменьшается при увеличении нагрузки, что приводит к увеличению ее вязкости.

В этих случаях, в частности, при больших деформациях наблюдается увеличение эффективной вязкости с увеличением градиента скорости (дилатансия – уменьшение плотности структуры при ее деформировании под действием приложенных напряжений – например, при начальной стадии размешивания крахмала в воде, в керамических массах, т.е. в порошках и уплотненных дисперсных материалах).

В дисперсной системе с большим содержанием твердой фазы при малых нагрузках дисперсионная среда играет роль смазки, уменьшая силу трения и вязкость системы, прежде чем частицы начнут двигаться, их упаковка становится более рыхлой, и система увеличивается в объеме, вязкость уменьшается. С увеличением напряжения сдвига твердые частицы вступают в контакт, что вызывает увеличение силы трения и вязкость системы возрастает.

Системы, в которых наблюдается зависимость вязкости от напряжения сдвига, называются аномальными или неньютоновскими.

Разнообразие структур в реальных дисперсных системах не позволяет четко разделить их на 2 вида: коагуляционные и конденсационно-кристаллизационные. Предложенная Ребиндером классификация помогает связать механические свойства тел с их строением.

Для нестационарных неньютоновских жидкостей, отличающихся зависимостью реологических свойств от времени, характерны явления тиксотропии и реопексии. Тиксотропность - способность структурированной системы восстанавливать во времени свои прочностные свойства после её механического разрушения. Восстановление структуры обычно обнаруживают по увеличению вязкости системы, поэтому явление тиксотропии можно определить как уменьшение вязкости системы во времени при наложении нагрузки и постепенный рост вязкости после снятия нагрузки. Реопексия - явление, обратное тиксотропии - возникновение и упрочнение структуры во времени в результате механического воздействия.