2. По полярности

В зависимости от полярности поверхности различают полярные и неполярные адсорбенты.

Полярные адсорбенты содержат на своей поверхности полярные группы, такие как –ОН, -СООН, -SO₃OHи т.д. Примерами могут служить силикагель, оксид алюминия, аэрогель и т.п. Неполярные адсорбенты не содержат полярных групп. Это - сажа, активированный уголь, никель Ренея и т.п. Следует отметить, что путём модифицирования можно изменить свойств поверхности. Так, частичным окислением поверхности получают полярные сажи.

полярные — бумага, силикагель, алюмогель

неполярные — сажа, угли

3. По размеру пор

В зависимости от преобладания пор того или иного размера(среднего радиуса пор) адсорбенты классифицируют на:

1. макропористые – в них преобладают макропоры с диаметрами 100 – 200 нм. Примером может служить технический углерод;

2. мезопористые– в них преобладают мезопоры с диаметрами 2 - 100 нм. Это - шариковый оксид алюминия, алюмосиликаты и т.п.;

3. микропористые– в них преобладают микропоры с диаметром < 5 нм – активированный уголь, бемитный гидроксид алюминия, силикагели и т.п.

В большинстве перечисленных систем имеется бипористая структура: первичные микропоры внутри частиц (глобул) и вторичные мезо- и макропоры, образуемые пространством между частицами.

Пористость (П) определяется по формуле (2.99): П = V_пор/V_{адсорбента}

Макропоры переходнопористые микропористые

d = 100 — 200 нм 2 — 100 нм 0,5 — 1,5-2,0 нм

S_уд = 0,2—2 м²/г 10 — 500 м²/г 500 — 1000 м²/г

0. 2.4.5.2. Влияние кривизны поверхности на равновесие фаз

До сих пор мы рассматривали поверхностные явления в системах, в которых сосуществующие фазы разделены плоской межфазной границей (с большим радиусом кривизны — см. ниже). Искривление поверхности раздела фаз вносит изменения в термодинамические свойства системы и обусловливает некоторые важные эффекты, относящиеся к числу капиллярных явлений.

Давления в контактирующих фазах, разделенных плоской поверхностью в условиях равновесия одинаковы. В отличие от этого давления в фазах, разделенных искривленной поверхностью, например, сферической, отличаются.

Пример. В этом легко убедиться на примере образования мыльных пузырей: если оставить в трубочке открытым отверстие, то под действием большего давления в пузырьке воздух начнет выходить, а размеры пузырька уменьшатся вплоть до его исчезновения. При этом уменьшаются поверхность пузырька и связанная с ней поверхностная энергия.

Что избыточное давление возрастает с уменьшением радиуса пузырька (радиуса кривизны — см. далее) можно доказать, выдув два пузырька разных размеров, а затем их соединив: маленький пузырек будет уменьшаться, а большой увеличиваться вплоть до полного перехода воздуха из малого в большой.

Вспомним, что из-за избыточной поверхностной энергии жидкая фаза благодаря своей подвижности приобретает сферическую форму в условиях невесомости. Вода в реках, морях, озёрах имеет плоскую поверхность только потому, что действует сила тяжести (F). С уменьшением количества жидкости её роль снижается, т.к. F ~ d³ (V), а S ~ d² ; S_уд=↑. Возрастающая роль поверхностной энергии проявляется в появлении кривизны поверхности жидкой фазы.

1. Рассмотрим изменение давления насыщенного пара жидкостипри искривлении её поверхности (насыщенным называют пар, находящийся в равновесии со своей жидкостью) в трёх случаях: поверхность жидкости плоская, поверхность жидкости вогнутая и поверхность жидкости выпуклая (рис.2.29)

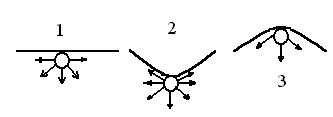
Рис.2.29. Межмолекулярные взаимодействия на искривлённой поверхности жидкости

Наиболее интенсивные взаимодействия в поверхностном слое жидкости наблюдаются в случае вогнутой поверхности (2). Здесь любая поверхностная молекула окружена максимальным числом «соседей». Выход её в газовую фазу в данном случае потребует наибольших затрат энергии. Поэтому следует ожидать, что над вогнутой поверхностью давление насыщенного пара будет минимальным.

В случае выпуклой поверхности жидкости (3) число молекул, окружающих выделенную поверхностную молекулу, минимально и, соответственно, давление насыщенного пара будет максимальным.Среднее положение занимает плоская поверхность.

Таким образом, давление насыщенного пара зависит от кривизны поверхности жидкости: над выпуклой поверхностью оно больше, а над вогнутой оно меньше, чем над плоской. И чем больше кривизна поверхности, тем сильнее отличаются друг от друга давления над плоской и искривленной поверхностью.

Рассмотрим результат влияния кривизны поверхности раздела между 2 несмешивающимися жидкостями на внутреннее давление Р в контактирующих фазах.

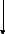
ΔР

r

Рис. 2.30. Влияние кривизны поверхности раздела на внутреннее давление

Кривизна поверхности вызывает изменение площади и положения межфазной поверхности, что можно выразить изменением поверхностной энергии (σ dS), изменяются объёмы фаз 1 и 2: dV₁= -dV_2, что ведет к изменению энергий ΔЕ фаз 1 и 2 на ΔЕ₁= р₁dV₁ и ΔЕ₂₌р₂dV₂ (р₁ и р₂ — внутренние давления внутри фаз).

Соотношение между поверхностной энергий и «объёмной» можно записать с помощью обобщенного уравнения 1 и 2-го законов термодинамики относительно энергии Гельмгольца F при Т=const:

dF=- р₁dV₁ - р₂dV₂ + σ dS (2.100)

При равновесии фаз ΔF=0, тогда

(р₁ - р₂) dV₂+ σ dS = 0, ΔР= р₂ - р₁= σ _(2.101)

— кривизна поверхности. Чем больше поверхностное натяжение, тем выше влияние кривизны поверхности. Вывод из уравнения следующий:

Фазы, разделённые искривлённой поверхностью, могут находиться в равновесии только при разных давлениях Р внутри фаз.

В фазе, имеющей «+» кривизну давление выше, чем в фазе с «—» кривизной. Стремление межфазного поверхностного натяжения сократить поверхность ведет к увеличению давления во второй фазе. Эту разность ΔРможно представить как равнодействующую силσ, сходящихся в т.О.ΔРнаправлена перпендикулярно к поверхности в центр кривизны.

ΔР = Р_σ — разность давлений в соседних фазах, разделённых искривленной поверхностью, называетсякапиллярным давлением.

Если Р₁=const(напр. атмосферное), тоΔР — изменение давлений в конденсированной фазе с кривизной (Р_r) по сравнению с давлением в такой же фазе под ровной поверхностью (Р_∞) равно :ΔР= Р_r- Р_∞.

Рассчитаем его для разных поверхностей:

Для сферической поверхности== 2/r: (8πr dr/4πr² dr) (2.102)

ΔР=2σ/r — (2.103)

- уравнение Лапласа^(*), рассчитывающее избыточное лапласовское давление.Чем меньше радиус, тем больше капиллярное давление.

Для капли воды с r=10^-6 м ΔР=15 МПа (1,5 атм)— это немного — доля его во внутреннем давлении (приблизительно 1000 МПа) =0,1%, но достаточна для образования сферы. Такое жеΔРхарактерно и для пузырьков воздуха в жидкости. Для каплиr=10^-9 м ΔР уже составляет = 10%.

Цилиндрическая поверхностьдлинойlи радиусомrимеет кривизну, равную

==1/r ΔР= σ/r (2.104)

Для поверхности неправильной формы используется представление о средней кривизне поверхности по уравнению Н=1/2(1/r₁+1/r₂), где r₁ и r₂ — кривизна главных нормальных сечений.

ΔРнаправлено всегда в центр кривизны. Если он находится вне жидкости, то кривизна отрицательная «—», (внутреннее давление жидкости уменьшается, жидкость растягивается), а если в жидкости, то положительная «+» (внутреннее давление жидкости увеличивается, жидкость сжимается).

Избыточное давление лежит в основе метода по расчету поверхностных натяжений жидкости — метод максимального давления в пузырькепо формуле:σ=к ΔР, к — константа прибора.

Пузырек воздуха, растущий на конце капилляра под действием разности давлений между атмосферой и прибором, образует полусферу. В момент, когда капиллярное давление не может уравновесить приложенной разности давленийΔР, пузырек отрывается:ΔР>2σ/r_о, где r_о— радиус капилляра. Максимальное давление соответствует образованию полусферы пузырька воздуха радиусом, равным радиусу капилляра, и его отрыву от кольца.