0. 2.4.5.5. Классификация изотерм адсорбции

Согласно Брунауэру, изотермы адсорбции газов и паров можно представить в виде следующих типов:

1 2 3

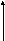
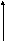
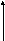
А

1 1 р/р_о

1. —мономолекулярная адсорбция, описывается уравнением Ленгмюра (Фрейндлиха, Темкина и т.д.)

2. — полимолекулярная адсорбция, уравнение БЭТ при С>20 (взаимодействие между адсорбентом и адсорбатом больше, чем между молекулами адсорбата на поверхности адсорбента

3. — полимолекулярная адсорбция, уравнение БЭТ при С<2 (взаимодействие между адсорбентом и адсорбатом меньше, чем между молекулами адсорбата на поверхности адсорбента.

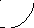
45 6

А

1 1 1 р/р_о

4 — =2, но осложненная капиллярной конденсацией, наблюдается петля адсорбционно-десорбционного гистерезиса

5 — =3, но осложненная капиллярной конденсацией, наблюдается петля адсорбционно-десорбционного гистерезиса

6 — такой вариант кривой возможен при строго послойной адсорбции.

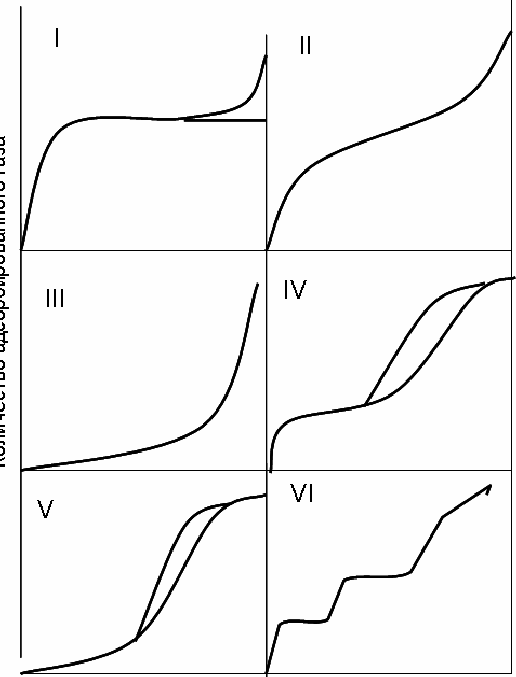
Рис.2.34. Изотермы полимолекулярной адсорбции

0. 2.4.6. Адсорбция из растворов на твердых адсорбентах

2.4.6.1. Молекулярная адсорбция

Речь идет об адсорбции из растворов неэлектролитов или слабых электролитов. Эти вещества адсорбируются в виде молекул. Особенность такой адсорбции в том, что поверхность адсорбента заполнена молекулами растворителя или адсорбата. Растворенное вещество может адсорбироваться, только вытесняя из поверхностного слоя молекулы растворителя, при этом происходит обменнаяадсорбция.

(2.4.6.1.1.) Модель идеального двумерного раствора адсорбата и растворителя (этот материал не даю)

Существует ряд моделей адсорбции молекул из разбавленных растворов.

Первая модель предполагает, что адсорбция сводится в образованию монослоя, прилегающего к поверхности адсорбента. Остальные слои — обычный раствор. Этот случай напоминает хемосорбцию газов, но с небольшой теплотой адсорбции и приводит к описанию адсорбции уравнением Ленгмюра

(Г=Г_∞ вс /1+ вс) или Фрейндлиха.

Вторая модель рассматривает адсорбцию как полимолекулярный слой, находящийся в монотонно спадающем потенциальном поле твердого адсорбента — уравнение БЭТ.

Модель идеального двумерного раствора адсорбата и растворителя предполагает:

1. поверхность однородна

2. площадь, занимаемая молекулой адсорбата равна площади, занимаемой молекулой растворителя

3. взаимодействие между всеми молекулами одинаковы

4. адсорбция мономолекулярна

Рассмотрим обмен между молекулами как квазихимическую реакцию:с константой обмена.

Константа адсорбционного равновесия этой реакции (константа обмена) равна:

_(2.108)

В разбавленных растворах можно считать N_A=const

(2.109)

коэффициент активности равен произведению концентрации на коэффициент активности a=Nγ, , поэтому константа k_а=k k_γ. (k — концентрационная константа). Константу коэффициентов активности в разбавленном растворе можно считать равной единице: k_γ=1, тогда:

(2.110)

— (2.111)

общее уравнение изотермы адсорбции из бинарных растворов с константой обмена,

Анализ уравнения показывает, что при N_A →0 . Рассмотрим графики изотерм адсорбции компонента:

`````1

3

2

1 N<sub>A</sub>

Рис. 2.35. Изотермы адсорбции растворенного компонента в растворе

Кривая 1 отвечает условию k >> 1 и полученное уравнение приобретает вид уравнения (при малых концентрациях растворенного компонента):

т.е. рассмотренная модель приводит к уравнению вида уравнения Ленгмюра:

При k<<1 (кривая 2) получаем уравнение вида

Если k≈1, т.е. величины сродства компонентов к адсорбенту близки, то на форму изотермы влияет коэффициент k<sub>γ</sub>.

Если поверхностный слой не идеален, то надо учитывать k<sub>γ</sub> адсорбата и растворителя. Если поверхность неоднородна, используют уравнения Темкина и Фрейндлиха.

продолжение, если не давать модель