3.3. Седиментационно-диффузионное равновесие. Седиментационная устойчивость

Процесс седиментации постепенно приводит дисперсную систему к упорядоченному состоянию, т.к. оседающие частицы располагаются в соответствии с их размерами. Через какое-то время все частицы могли бы осесть, но этому препятствует броуновское движение и диффузия, стремящиеся распределить все частицы равномерно по всему объему.

Между процессами диффузии и седиментации устанавливается седиментационно-диффузионное равновесие, которое характеризуется однородным распределением частиц по высоте столба. Под действием силы тяжести (или силы Архимеда) начнётся седиментация частиц. Седиментационный поток направлен ко дну сосуда, и он равен:

, (3.14)

где U – скорость движения частиц,  – плотность частиц фазы, ₀ – плотность среды, r – радиус частицы, С – концентрация частиц в сосуде, g – ускорение свободного падения.

Седиментация приведет к тому, что у дна сосуда концентрация частиц фазы станет выше, чем в верхней его части. В результате возникнет градиент концентрации частиц фазы по высоте h сосуда: . Появление градиента концентрации приведёт к диффузии частиц, диффузионный потокJ_d направлен вверх и он равен:

(3.15 )

Чем интенсивнее идет седиментация, тем больше становится градиент концентрации и тем значительней диффузионный поток. Наконец, при каком-то градиенте концентрации (распределении частиц фазы по высоте сосуда) скорости обоих потоков сравняются (в любом поперечном сечении сосуда число частиц, опускающихся вниз равно их числу, поднимающемуся вверх). Установившееся состояние системы носит название седиментационно-диффузионного равновесия.

С увеличением радиуса j_сед увеличивается (т.к. пропорционаленr²), а диффузионный поток уменьшается (т.к. пропорционален 1/r), j_сед >> j_d, который можно не учитывать.

Если j_d>>j_сед(для ультрамикрогетерогенных систем), седиментацией можно пренебречь.

Если приравнять скорости потоков:

= (3.16)

вместо Dподставить его выражение из (3.6), принять, что частицы имеют сферическую форму, и проинтегрировать полученное уравнение, то можно получить закон распределения частиц по высоте в равновесном состоянии, аналогичный известной барометрической формуле Лапласа⁽³⁶⁾для газов в атмосфере:

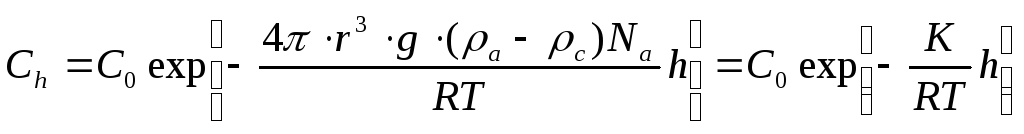(3.17)

Здесь С_h – концентрация частиц фазы на высоте сосуда h, С₀ – концентрация частиц у дна сосуда.

Если вместо концентрации дисперсной фазы С записать давление Р, то получим известную барометрическую формулу Лапласа^(*), характеризующую распределение давление газа по высоте. Уравнение Лапласа называетсягипсометрическим законом (hypsos – высота).Для золей наблюдается более резкая зависимость концентрации по высоте, чем для молекул газа.

Рассмотрим результаты расчетов.

Высоту, на которой концентрация молекул или частиц уменьшается в 2 раза, обозначим через h_1/2:

r	0,27 нм (газ)	230 нм сусп. гуммигута	М=40000а.е.м. Р-р макромолекул	1,86 нм золь золота
h1/2	5-5,5 км	30 мкм	20 м	2,15 м

Гипсометрический закон Лапласа был экспериментально подтвержден Перреном^(*)(1910). Он изучал в вертикальном микроскопе распределение суспензии гуммигута сr=212 нм. Через каждые 30 мкм число частиц в поле зрения уменьшалось ровно в 2 раза.

По формуле Лапласа было рассчитано значение числа Авогадро N_A= 6,82 10²³ .

За эти опыты, доказывающие победу атомизма и отличавшиеся остроумием, точностью и простотой, Перрену в 1926 г. была присуждена Нобелевская премия.

Следует отметить, что седиментационо - диффузионное равновесие устанавливается очень медленно: время установления пропорционально 1/r². В опытах Перрена постоянные значения С_h/С₀ устанавливались лишь в течение недели.